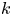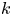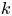1. Introduction
Bony's sharp maximum principle [Reference Bony6] describes the propagation of minima for supersolutions of degenerate elliptic operators in all the directions that can be reached through the so-called subunit vectors that characterize the operator. In this paper we show that in the nonlocal context, for some fully nonlinear degenerate operators with nonhomogenous diffusion, this is even more true.
We shall investigate two families of operators that we now introduce: given a direction $\xi \in \mathbb {R}^N$![]() and a function $u:\mathbb {R}^N\mapsto \mathbb {R}$
and a function $u:\mathbb {R}^N\mapsto \mathbb {R}$![]() , smooth enough, let
, smooth enough, let

where $s\in (0,1)$![]() and $C_s$
and $C_s$![]() is a normalizing constant such that $\mathcal {I}_\xi u(x)\to \left \langle D^2u(x)\xi,\xi \right \rangle$
is a normalizing constant such that $\mathcal {I}_\xi u(x)\to \left \langle D^2u(x)\xi,\xi \right \rangle$![]() as $s\to 1^-$
as $s\to 1^-$![]() . The so-called $k$
. The so-called $k$![]() -th fractional truncated Laplacian is defined by
-th fractional truncated Laplacian is defined by

where ${\mathcal {V}}_k$![]() denotes the family of $k$
denotes the family of $k$![]() -dimensional orthonormal sets in $\mathbb {R}^N$
-dimensional orthonormal sets in $\mathbb {R}^N$![]() , while the $k$
, while the $k$![]() -th fractional eigenvalue, is given by
-th fractional eigenvalue, is given by
As it was already pointed out in [Reference Birindelli, Galise and Schiera4, Reference Birindelli, Galise and Topp5], these operators do not satisfy the strong maximum principle in the sense that there exists nonnegative supersolutions that reach their minimum. More precisely, if $\Omega$![]() is an open subset of $\mathbb {R}^N$
is an open subset of $\mathbb {R}^N$![]() and $k< N$
and $k< N$![]() , then there exist nonnegative viscosity supersolutions $u\in LSC(\mathbb {R}^N)$
, then there exist nonnegative viscosity supersolutions $u\in LSC(\mathbb {R}^N)$![]() of
of
or of
verifying the conditions
where $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$![]() is the positivity set of $u$
is the positivity set of $u$![]() .
.
The main purpose of this paper is to give a characterization of $U$![]() , for both classes of operators.
, for both classes of operators.
Let us point out that if $k=N$![]() in (1.2)–(1.3), or if the infimum is replaced by the supremum in (1.2), then the corresponding operators satisfy the strong maximum principle, in which case the alternative claim $U\cap \Omega =\emptyset$
in (1.2)–(1.3), or if the infimum is replaced by the supremum in (1.2), then the corresponding operators satisfy the strong maximum principle, in which case the alternative claim $U\cap \Omega =\emptyset$![]() or $U\cap \Omega =\Omega$
or $U\cap \Omega =\Omega$![]() holds, see [Reference Birindelli, Galise and Schiera4, theorem 4.3 and proposition 4.7] for details.
holds, see [Reference Birindelli, Galise and Schiera4, theorem 4.3 and proposition 4.7] for details.
Before describing the results we obtain, we wish to mention that we are in the context of nonlocal viscosity solutions, classical references for the definition of viscosity solutions are [Reference Barles and Imbert1, Reference Caffarelli and Silvestre7]; see also [Reference Birindelli, Galise and Topp5] for a discussion on the notion of viscosity solutions for operators (1.2) and (1.3). It is important to underline the fact that for those operators the nonlocal diffusion is along $k$![]() one-dimensional sets. Nonlocal operators with nonlocality in subdimensional sets have been considered in other contexts; in particular, Bass and Chen in [Reference Bass and Chen2], using a probabilistic approach, prove some Hölder regularity results for solutions of equations involving operators that are sums of operators like (1.1) along $N$
one-dimensional sets. Nonlocal operators with nonlocality in subdimensional sets have been considered in other contexts; in particular, Bass and Chen in [Reference Bass and Chen2], using a probabilistic approach, prove some Hölder regularity results for solutions of equations involving operators that are sums of operators like (1.1) along $N$![]() orthogonal directions. Interestingly the regularity of the solution holds even if Harnack's inequality does not. Instead Endal, Ignat and Quiros in [Reference Endal, Ignat and Quiros9] consider the heat equation for a very large class of diffusion terms that include nonlocal operators such as those of Bass and Chen.
orthogonal directions. Interestingly the regularity of the solution holds even if Harnack's inequality does not. Instead Endal, Ignat and Quiros in [Reference Endal, Ignat and Quiros9] consider the heat equation for a very large class of diffusion terms that include nonlocal operators such as those of Bass and Chen.
We now describe the sharp maximum principle we obtain in the case of the nonlocal truncated Laplacians (1.2). We will prove in theorem 2.1 that if $U$![]() is the positivity set of a supersolution of (1.4), then $U$
is the positivity set of a supersolution of (1.4), then $U$![]() satisfies the following geometric condition $G_{\Omega,U,k}$
satisfies the following geometric condition $G_{\Omega,U,k}$![]() .
.
Definition 1.1

Furthermore, the ‘vice versa’ is true in the sense that for any $\Omega$![]() and $U$
and $U$![]() , open subsets of $\mathbb {R}^N$
, open subsets of $\mathbb {R}^N$![]() , satisfying $G_{\Omega,U,k}$
, satisfying $G_{\Omega,U,k}$![]() it is possible to construct a supersolution whose positivity set coincide with $U$
it is possible to construct a supersolution whose positivity set coincide with $U$![]() , see theorems 2.3 and 2.5. These two properties somehow reflects the fact that the diffusion is along $k$
, see theorems 2.3 and 2.5. These two properties somehow reflects the fact that the diffusion is along $k$![]() orthogonal lines.
orthogonal lines.
In order to give a better understanding of this geometric condition, we show in theorem 2.7 that, if $\partial U$![]() is smooth, condition $G_{\Omega,U,k}$
is smooth, condition $G_{\Omega,U,k}$![]() implies that the sum of the largest $k$
implies that the sum of the largest $k$![]() principal curvatures at any point $x\in \Omega \cap \partial U$
principal curvatures at any point $x\in \Omega \cap \partial U$![]() is non negative.
is non negative.
In the case of the operator (1.2), i.e. $k$![]() -th fractional eigenvalue, the geometric condition of the positivity set is $\mathcal {G}_{\Omega,U,k}$
-th fractional eigenvalue, the geometric condition of the positivity set is $\mathcal {G}_{\Omega,U,k}$![]() .
.
Definition 1.2

Mutatis mutandis the results are the same as for $\mathcal {I}^{-}_{k}$![]() . This condition, which is in fact stronger than $G_{\Omega,U,k}$
. This condition, which is in fact stronger than $G_{\Omega,U,k}$![]() as it will be seen later, is different in nature because even though the operator is defined only through one-dimensional integrals and so with one-dimensional diffusion, the sets involved in the propagation of the minimum are $k$
as it will be seen later, is different in nature because even though the operator is defined only through one-dimensional integrals and so with one-dimensional diffusion, the sets involved in the propagation of the minimum are $k$![]() -dimensional affine spaces.
-dimensional affine spaces.
Also, if $\partial U$![]() is smooth, $\mathcal {G}_{\Omega,U,k}$
is smooth, $\mathcal {G}_{\Omega,U,k}$![]() implies that the $(N-k)$
implies that the $(N-k)$![]() -th principal curvature is nonnegative. Furthermore, when $k=N-1$
-th principal curvature is nonnegative. Furthermore, when $k=N-1$![]() , $\mathcal {G}_{\mathbb {R}^{N},U,N-1}$
, $\mathcal {G}_{\mathbb {R}^{N},U,N-1}$![]() implies that the connected components of $U$
implies that the connected components of $U$![]() are convex sets, see theorems 3.5 and 3.6.
are convex sets, see theorems 3.5 and 3.6.
It is inevitable to compare the results that hold in the nonlocal case with those obtained for the differential operators to which these operators tend when $s$![]() goes to 1. It is easy to see that, under reasonable conditions on the function $u$
goes to 1. It is easy to see that, under reasonable conditions on the function $u$![]() , $\mathcal {I}^{-}_{k}u$
, $\mathcal {I}^{-}_{k}u$![]() converges pointwise to ${\mathcal {P}}^-_k(D^2u):=\lambda _1(D^2u)+\ldots +\lambda _k(D^2u)$
converges pointwise to ${\mathcal {P}}^-_k(D^2u):=\lambda _1(D^2u)+\ldots +\lambda _k(D^2u)$![]() , while $\mathcal {I}_ku$
, while $\mathcal {I}_ku$![]() converges to $\lambda _k(D^2u)$
converges to $\lambda _k(D^2u)$![]() , where $\lambda _1(D^2u)\leq \lambda _2(D^2u)\leq \ldots \leq \lambda _N(D^2u)$
, where $\lambda _1(D^2u)\leq \lambda _2(D^2u)\leq \ldots \leq \lambda _N(D^2u)$![]() denote the eigenvalues of the Hessian $D^2u$
denote the eigenvalues of the Hessian $D^2u$![]() arranged in nondecreasing order. Among other things, for these very degenerate elliptic operators, some characterizations of the positivity set were given in [Reference Birindelli, Galise and Ishii3].
arranged in nondecreasing order. Among other things, for these very degenerate elliptic operators, some characterizations of the positivity set were given in [Reference Birindelli, Galise and Ishii3].
Remarkably, the conditions on the principal curvatures of $\partial U$![]() , which are implied by $G_{\Omega,U,k}$
, which are implied by $G_{\Omega,U,k}$![]() or by ${\mathcal {G}}_{\Omega,U,k}$
or by ${\mathcal {G}}_{\Omega,U,k}$![]() , are the same in the local case and in the nonlocal case. But differently from the local case, see [Reference Birindelli, Galise and Ishii3, theorem 11], the statement of theorem 3.6 cannot be reversed. There exist open sets, with convex connected components, for which ${\mathcal {G}}_{\mathbb {R}^N,U,N-1}$
, are the same in the local case and in the nonlocal case. But differently from the local case, see [Reference Birindelli, Galise and Ishii3, theorem 11], the statement of theorem 3.6 cannot be reversed. There exist open sets, with convex connected components, for which ${\mathcal {G}}_{\mathbb {R}^N,U,N-1}$![]() is not true. A very simple example is given by the union of disjoint open balls in $\mathbb {R}^N$
is not true. A very simple example is given by the union of disjoint open balls in $\mathbb {R}^N$![]() .
.
With a different aim, but with a similar point of view, Del Pezzo, Quaas and Rossi in [Reference Del Pezzo, Quaas and Rossi8] have introduced a notion of fractional convexity and they define the $s$![]() -convex envelope through ${\mathcal {I}}_1u$
-convex envelope through ${\mathcal {I}}_1u$![]() , in similarity with the result of Oberman and Silvestre [Reference Oberman and Silvestre10].
, in similarity with the result of Oberman and Silvestre [Reference Oberman and Silvestre10].
2. The case of $\mathcal {I}^{-}_{k}$
Let $U$![]() and $\Omega$
and $\Omega$![]() be open subsets of $\mathbb {R}^N$
be open subsets of $\mathbb {R}^N$![]() . Since $G_{\Omega,U,k}$
. Since $G_{\Omega,U,k}$![]() is trivial if $U=\emptyset$
is trivial if $U=\emptyset$![]() , henceforth we shall assume that $U$
, henceforth we shall assume that $U$![]() is nonempty.
is nonempty.
Theorem 2.1 Assume that $u\in LSC(\mathbb {R}^N)$![]() is a bounded and nonnegative $($
is a bounded and nonnegative $($![]() in $\mathbb {R}^N)$
in $\mathbb {R}^N)$![]() viscosity supersolution of
viscosity supersolution of
such that $\min _\Omega u=0$![]() . Then its positivity set $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$
. Then its positivity set $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$![]() satisfies $G_{\Omega,U,k}$
satisfies $G_{\Omega,U,k}$![]() .
.
Proof. Let $x_0\in \Omega \backslash U$![]() . Then $u(x_0)=0$
. Then $u(x_0)=0$![]() . We test $u$
. We test $u$![]() from below at $x_0$
from below at $x_0$![]() by
by

From the inequality
we infer that, for any $n\in \mathbb {N}$![]() , there exists an orthonormal frame $\left \{\xi _1(n),\ldots,\xi _k(n)\right \}$
, there exists an orthonormal frame $\left \{\xi _1(n),\ldots,\xi _k(n)\right \}$![]() such that
such that

where $\chi _{(\frac 1n,+\infty )}$![]() denotes the characteristic function of the interval $(\frac 1n,+\infty )$
denotes the characteristic function of the interval $(\frac 1n,+\infty )$![]() .
.
Up to a subsequence we can further assume that
and that $\left \{\bar \xi _1,\ldots,\bar \xi _k\right \}\in {\mathcal {V}}_k$![]() .
.
Using Fatou's lemma in (2.2) we obtain

Since for any $\tau >0$![]() we have $\chi _{(\frac 1n,+\infty )}(\tau )\to \chi _{(0,+\infty )}(\tau )$
we have $\chi _{(\frac 1n,+\infty )}(\tau )\to \chi _{(0,+\infty )}(\tau )$![]() as $n\to +\infty$
as $n\to +\infty$![]() and
and
by lower semincontinuity, then we infer from (2.3) that

Moreover, $u\geq 0$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() by assumption, hence by (2.4) we conclude that
by assumption, hence by (2.4) we conclude that
that is $x_0+\tau \bar \xi _i\notin U$![]() for any $\tau \in \mathbb {R}$
for any $\tau \in \mathbb {R}$![]() and any $i=1,\ldots,k$
and any $i=1,\ldots,k$![]() .
.
Remark 2.2 Theorem 2.1 excludes the existence of bounded supersolutions $u\in LSC(\mathbb {R}^N)$![]() of
of
such that
Conversely, any open subset $U$![]() satisfying $G_{\Omega,U,k}$
satisfying $G_{\Omega,U,k}$![]() coincide with the positivity set of a supersolution $u$
coincide with the positivity set of a supersolution $u$![]() of the equation (1.4).
of the equation (1.4).
Theorem 2.3 Assume that $U$![]() is an open set satisfying $G_{\Omega,U,k}$
is an open set satisfying $G_{\Omega,U,k}$![]() . Then there exists a nonnegative and bounded (in $\mathbb {R}^N$
. Then there exists a nonnegative and bounded (in $\mathbb {R}^N$![]() ) supersolution $u\in LSC(\mathbb {R}^N)$
) supersolution $u\in LSC(\mathbb {R}^N)$![]() of
of
such that
Proof. Let us define $u\in LSC(\mathbb {R}^N)$![]() by
by
It is clear that $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$![]() . Moreover, since $\Omega \backslash U\neq \emptyset$
. Moreover, since $\Omega \backslash U\neq \emptyset$![]() by definition of $G_{\Omega,U,k}$
by definition of $G_{\Omega,U,k}$![]() , it holds that $\min _\Omega u=0$
, it holds that $\min _\Omega u=0$![]() .
.
To prove that $u$![]() is a viscosity supersolution, let $x_0\in \Omega$
is a viscosity supersolution, let $x_0\in \Omega$![]() . If $x_0\in \Omega \cap U$
. If $x_0\in \Omega \cap U$![]() , then $u(x_0)=1$
, then $u(x_0)=1$![]() . Since $U$
. Since $U$![]() is open, the function $u$
is open, the function $u$![]() is in fact constant in a neighbourhood of $x_0$
is in fact constant in a neighbourhood of $x_0$![]() . Hence, for any $\xi \in \mathbb {R}^N$
. Hence, for any $\xi \in \mathbb {R}^N$![]() , with $|\xi |=1$
, with $|\xi |=1$![]() , $\mathcal {I}_\xi u(x_0)$
, $\mathcal {I}_\xi u(x_0)$![]() is well defined and
is well defined and

considering that $0\leq u(x)\leq 1$![]() for any $x\in \mathbb {R}^N$
for any $x\in \mathbb {R}^N$![]() . Then we infer that the inequality
. Then we infer that the inequality
holds in classical, and so in the viscosity, sense at $x_0\in \Omega \cap U$![]() .
.
Assume now that $x_0\in \Omega \backslash U$![]() , so that $u(x_0)=0$
, so that $u(x_0)=0$![]() . In this case $u$
. In this case $u$![]() can be discontinuous at $x_0$
can be discontinuous at $x_0$![]() depending on whether $x_0\in \Omega \cap \partial U$
depending on whether $x_0\in \Omega \cap \partial U$![]() or not.
or not.
To check that the inequality $\mathcal {I}^{-}_{k}u(x_0)\leq 0$![]() holds in the viscosity sense, let $\varphi \in C^2(\overline {B_\delta (x_0)})$
holds in the viscosity sense, let $\varphi \in C^2(\overline {B_\delta (x_0)})$![]() , $\delta >0$
, $\delta >0$![]() , be such that
, be such that
Consider the function

Using the hypothesis $G_{\Omega,U,k}$![]() , there exists an orthonormal frame $\left \{\bar \xi _1,\ldots,\bar \xi _k\right \}$
, there exists an orthonormal frame $\left \{\bar \xi _1,\ldots,\bar \xi _k\right \}$![]() , depending on $x_0$
, depending on $x_0$![]() , such that
, such that
Thus, by (2.5)–(2.6), we conclude

Remark 2.4 As a consequence of theorem 2.1 and of the proof of theorem 2.3, if $u\in LSC(\mathbb {R}^N)$![]() is a nonnegative and bounded (in $\mathbb {R}^N$
is a nonnegative and bounded (in $\mathbb {R}^N$![]() ) viscosity supersolution of
) viscosity supersolution of
then the characteristic function $\chi _U$![]() of its positivity set $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$
of its positivity set $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$![]() is in turn viscosity supersolution of the same equation, that is
is in turn viscosity supersolution of the same equation, that is
Next theorem provides the existence of a Lipschitz continuous entire supersolution with a prescribed positivity set $U$![]() satisfying the property $G_{\mathbb {R}^N,U,k}$
satisfying the property $G_{\mathbb {R}^N,U,k}$![]() .
.
Theorem 2.5 Assume that $U$![]() is an open and bounded subset of $\mathbb {R}^N$
is an open and bounded subset of $\mathbb {R}^N$![]() that satisfies $G_{\mathbb {R}^N,U,k}$
that satisfies $G_{\mathbb {R}^N,U,k}$![]() . Then there exists a nonnegative and bounded viscosity supersolution $u\in \mathrm {Lip}(\mathbb {R}^N)$
. Then there exists a nonnegative and bounded viscosity supersolution $u\in \mathrm {Lip}(\mathbb {R}^N)$![]() of
of
such that $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$![]() .
.
Proof. We define
Clearly $u$![]() is bounded and Lipschitz in $\mathbb {R}^N$
is bounded and Lipschitz in $\mathbb {R}^N$![]() . Moreover, since $U$
. Moreover, since $U$![]() is open, $u(x)>0$
is open, $u(x)>0$![]() if, and only if, $x\in U$
if, and only if, $x\in U$![]() .
.
To check that $u$![]() is a viscosity supersolution of (2.7), let $x_0\in \mathbb {R}^N$
is a viscosity supersolution of (2.7), let $x_0\in \mathbb {R}^N$![]() and let $\varphi \in C^2(\overline {B_\delta (x_0)})$
and let $\varphi \in C^2(\overline {B_\delta (x_0)})$![]() , $\delta >0$
, $\delta >0$![]() , be such that
, be such that
Setting

we have to prove that $\mathcal {I}^{-}_{k}\psi (x_0)\leq 0$![]() .
.
We choose $y_0\in \mathbb {R}^N\backslash U$![]() , depending on $x_0$
, depending on $x_0$![]() , such that
, such that
Moreover, by the definition of $u$![]() , we have
, we have
Using (2.9)–(2.10) with $x=y+x_0-y_0$![]() and setting $\phi (y)=\varphi (y+x_0-y_0)$
and setting $\phi (y)=\varphi (y+x_0-y_0)$![]() , we then obtain
, we then obtain
Since $y_0\in \mathbb {R}^N\backslash U$![]() , by the assumption $G_{\mathbb {R}^N,U,k}$
, by the assumption $G_{\mathbb {R}^N,U,k}$![]() there exists an orthonormal frame $\left \{\bar \xi _1,\ldots,\bar \xi _k\right \}$
there exists an orthonormal frame $\left \{\bar \xi _1,\ldots,\bar \xi _k\right \}$![]() such that
such that
Then, from (2.11) and (2.12), we have
The above inequality implies that

Moreover, since $\phi (y_0\pm \tau \bar \xi _i)=\varphi (x_0\pm \tau \bar \xi _i)$![]() for $\tau \in [0,\delta )$
for $\tau \in [0,\delta )$![]() and $i=1,\ldots,k$
and $i=1,\ldots,k$![]() , we obtain
, we obtain

Now, we use the inequality
with the particular choice $x=x_0\pm \tau \bar \xi _i$![]() and $y=y_0\pm \tau \bar \xi _i$
and $y=y_0\pm \tau \bar \xi _i$![]() to infer that
to infer that
Thus,

The conclusion
Remark 2.6 The assumption $U$![]() bounded in the statement of theorem 2.5 has been used only to guarantee that $u(x)=\text {dist}(x,\mathbb {R}^N\backslash U)$
bounded in the statement of theorem 2.5 has been used only to guarantee that $u(x)=\text {dist}(x,\mathbb {R}^N\backslash U)$![]() was bounded. In this way, the maps
was bounded. In this way, the maps
are integrable outside the origin, for any direction $\xi$![]() and any $x\in \mathbb {R}^N$
and any $x\in \mathbb {R}^N$![]() .
.
In the case $U$![]() unbounded, using the Lipschitz continuity of $u$
unbounded, using the Lipschitz continuity of $u$![]() , the integrability of (2.15) far away from the origin, is still true, independently of $\xi$
, the integrability of (2.15) far away from the origin, is still true, independently of $\xi$![]() , provided $s>\frac 12$
, provided $s>\frac 12$![]() .
.
Another possibility to deal with general $U$![]() and without the restriction $s\in (\frac 12,1)$
and without the restriction $s\in (\frac 12,1)$![]() , is to replace $u(x)=\text {dist}(x,\mathbb {R}^N\backslash U)$
, is to replace $u(x)=\text {dist}(x,\mathbb {R}^N\backslash U)$![]() by
by
The details are left to the reader.
Let $u$![]() be a viscosity supersolution of
be a viscosity supersolution of
and suppose that the relative boundary $\Omega \cap \partial U$![]() of its positivity set $U$
of its positivity set $U$![]() is smooth. Then, denoting with
is smooth. Then, denoting with
the principal curvatures of $\Omega \cap \partial U$![]() at $x$
at $x$![]() , one has
, one has
This geometric property is a consequence of theorem 2.1 and the following
Theorem 2.7 Let $U$![]() be an open set verifying $G_{\Omega,U,k}$
be an open set verifying $G_{\Omega,U,k}$![]() and assume that $\Omega \cap \partial U$
and assume that $\Omega \cap \partial U$![]() is a $C^2$
is a $C^2$![]() -hypersurface. Then
-hypersurface. Then

Proof. Let $x_0\in \Omega \cap \partial U$![]() . By assumption, and by an orthogonal transformation, we may assume that $x_0=0$
. By assumption, and by an orthogonal transformation, we may assume that $x_0=0$![]() and that for some $r>0$
and that for some $r>0$![]()
where $x=(x',x_N)$![]() and
and
Moreover, the principal curvatures of $\Omega \cap \partial U$![]() at $x_0=0$
at $x_0=0$![]() are the eigenvalues of $D^2f(0')$
are the eigenvalues of $D^2f(0')$![]() .
.
Since $G_{\Omega,U,k}$![]() holds and $x_0=0\in \Omega \backslash U$
holds and $x_0=0\in \Omega \backslash U$![]() , then there exists $\left \{\bar \xi _i\right \}_{i=1}^k\in {\mathcal {V}}_k$
, then there exists $\left \{\bar \xi _i\right \}_{i=1}^k\in {\mathcal {V}}_k$![]() such that
such that
We claim that $\left \langle \bar \xi _i,e_N\right \rangle =0$![]() for any $i=1,\ldots,k$
for any $i=1,\ldots,k$![]() , where $e_N=(0',1)$
, where $e_N=(0',1)$![]() .
.
If not, then $\left \langle \bar \xi _i,e_N\right \rangle \neq 0$![]() for some $i\in \left \{1,\ldots,k\right \}$
for some $i\in \left \{1,\ldots,k\right \}$![]() . Replacing $\bar \xi _i$
. Replacing $\bar \xi _i$![]() with $-\bar \xi _i$
with $-\bar \xi _i$![]() if necessary, we can further suppose that $\left \langle \bar \xi _i,e_N\right \rangle >0$
if necessary, we can further suppose that $\left \langle \bar \xi _i,e_N\right \rangle >0$![]() . Since
. Since
we infer that for any $\tau$![]() positive and small enough
positive and small enough
Thus, using (2.18), we have that for any $\tau$![]() positive and small enough
positive and small enough
which contradicts (2.20).
Since $\left \langle \bar \xi _i,e_N\right \rangle =0$![]() , we can write
, we can write
Moreover, $\left \{\bar \xi '_1,\ldots,\bar \xi '_k\right \}$![]() is an orthonormal frame in $\mathbb {R}^{N-1}$
is an orthonormal frame in $\mathbb {R}^{N-1}$![]() .
.
Consider now, for $i=1,\ldots,k$![]() , the functions
, the functions
Using (2.18)–(2.19)–(2.20)–(2.21) we obtain that
Hence for any $i=1,\ldots,k$![]()
from which we conclude that

3. The case of $\mathcal {I}_k$
As it was mentioned in the introduction, for the operator $\mathcal {I}_k$![]() the right condition on the positivity set is $\mathcal {G}_{\Omega,U,k}$
the right condition on the positivity set is $\mathcal {G}_{\Omega,U,k}$![]() , see definition 1.2. We start the section giving an example of a bounded open set $U\subset \mathbb {R}^3$
, see definition 1.2. We start the section giving an example of a bounded open set $U\subset \mathbb {R}^3$![]() which satisfies the condition $G_{\mathbb {R}^3,U,2}$
which satisfies the condition $G_{\mathbb {R}^3,U,2}$![]() , but not $\mathcal {G}_{\mathbb {R}^3,U,2}$
, but not $\mathcal {G}_{\mathbb {R}^3,U,2}$![]() . Such an example can be easily generalized to $\mathbb {R}^N$
. Such an example can be easily generalized to $\mathbb {R}^N$![]() and $k< N$
and $k< N$![]() .
.
Example 3.1 Let
where $U_1$![]() and $U_2$
and $U_2$![]() are the two unit and open balls defined by
are the two unit and open balls defined by

Let us first show that condition $\mathcal {G}_{\mathbb {R}^3,U,2}$![]() is not satisfied. For this we consider, for $\varepsilon$
is not satisfied. For this we consider, for $\varepsilon$![]() positive and small enough, the point $P_\varepsilon =(0,\varepsilon,\sqrt {1-\varepsilon ^2})\notin U$
positive and small enough, the point $P_\varepsilon =(0,\varepsilon,\sqrt {1-\varepsilon ^2})\notin U$![]() . We claim that every two-dimensional plane $\pi$
. We claim that every two-dimensional plane $\pi$![]() passing through $P_\varepsilon$
passing through $P_\varepsilon$![]() has nonempty intersection with $U$
has nonempty intersection with $U$![]() . This is obvious if $\pi$
. This is obvious if $\pi$![]() is not the tangent plane to the unit sphere $\partial U_1=\left \{x^2+y^2+z^2=1\right \}$
is not the tangent plane to the unit sphere $\partial U_1=\left \{x^2+y^2+z^2=1\right \}$![]() , since $P_\varepsilon \in \partial U_1$
, since $P_\varepsilon \in \partial U_1$![]() . On the other hand, if $\pi$
. On the other hand, if $\pi$![]() is the tangent plane to $\partial U_1$
is the tangent plane to $\partial U_1$![]() at the point $P_\varepsilon$
at the point $P_\varepsilon$![]() , it is not difficult to see that
, it is not difficult to see that
for any $\varepsilon$![]() positive and sufficiently small. Hence $\mathcal {G}_{\mathbb {R}^3,U,2}$
positive and sufficiently small. Hence $\mathcal {G}_{\mathbb {R}^3,U,2}$![]() is not fulfilled at $P_\varepsilon$
is not fulfilled at $P_\varepsilon$![]() .
.
Now we prove that $U$![]() has the property ${G}_{\mathbb {R}^3,U,2}$
has the property ${G}_{\mathbb {R}^3,U,2}$![]() . Fix $(x_0,y_0,z_0)\notin U$
. Fix $(x_0,y_0,z_0)\notin U$![]() . If there exists a two-dimensional linear space $V\subset \mathbb {R}^3$
. If there exists a two-dimensional linear space $V\subset \mathbb {R}^3$![]() such that $((x_0,y_0,z_0)+V)\cap U=\emptyset,$
such that $((x_0,y_0,z_0)+V)\cap U=\emptyset,$![]() then we are done. Suppose now that for any linear space $V$
then we are done. Suppose now that for any linear space $V$![]() , with $\dim V=2$
, with $\dim V=2$![]() ,
,
In particular, this implies that
Otherwise, it is obvious that there exists a two-dimensional linear space $W$![]() such that
such that
By symmetry, we suppose in the following that $y_0\in (0,1)$![]() . A similar argument, with obvious changes, holds in the case $y_0\in (3,4)$
. A similar argument, with obvious changes, holds in the case $y_0\in (3,4)$![]() . We can pick $V$
. We can pick $V$![]() in such a way
in such a way
We then have that $((x_0,y_0,z_0)+V)\cap U_2\neq \emptyset \,.$![]() Note that $((x_0,y_0,z_0)+V)\cap U_2$
Note that $((x_0,y_0,z_0)+V)\cap U_2$![]() is a disc and that
is a disc and that
After a rigid transformation we can also assume that $(x_0,y_0,z_0)=(0,0,0)$![]() , $V$
, $V$![]() is spanned by $e_1=(1,0,0)$
is spanned by $e_1=(1,0,0)$![]() and $e_2=(0,1,0)$
and $e_2=(0,1,0)$![]() and that
and that
for some $\alpha >2$![]() and $\rho \in (0,1]$
and $\rho \in (0,1]$![]() . Now, it is immediate to see that
. Now, it is immediate to see that

are two orthogonal lines passing through $(x_0,y_0,z_0)$![]() and such that
and such that
Since $(x_0,y_0,z_0)\notin U$![]() is arbitrary, we conclude that $U$
is arbitrary, we conclude that $U$![]() has the property ${G}_{\mathbb {R}^3,U,2}$
has the property ${G}_{\mathbb {R}^3,U,2}$![]() .
.
Theorem 3.2 Assume that $u\in LSC(\mathbb {R}^N)$![]() is a bounded and nonnegative $($
is a bounded and nonnegative $($![]() in $\mathbb {R}^N)$
in $\mathbb {R}^N)$![]() viscosity supersolution of
viscosity supersolution of
such that $\min _\Omega u=0$![]() . Then its positivity set $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$
. Then its positivity set $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$![]() satisfies $\mathcal {G}_{\Omega,U,k}$
satisfies $\mathcal {G}_{\Omega,U,k}$![]() .
.
Proof. Let $x_0\in \Omega \backslash U$![]() . We proceed as in the proof of theorem 2.1 testing $u$
. We proceed as in the proof of theorem 2.1 testing $u$![]() from below at $x_0$
from below at $x_0$![]() by the sequence of function $\psi _n$
by the sequence of function $\psi _n$![]() defined in (2.1). Hence for any $n\in \mathbb {N}$
defined in (2.1). Hence for any $n\in \mathbb {N}$![]() , there exists a $k$
, there exists a $k$![]() -dimensional linear space $V=V(n)$
-dimensional linear space $V=V(n)$![]() such that
such that

Choose an orthonormal basis $\left \{\xi _1(n),\ldots,\xi _k(n)\right \}$![]() of $V$
of $V$![]() . Passing to a subsequence, we can also assume that
. Passing to a subsequence, we can also assume that
Let $\bar V=\text {span}\left \{\bar \xi _1,\ldots,\bar \xi _k\right \}$![]() . We have $\dim \bar V=k$
. We have $\dim \bar V=k$![]() . We claim that $\bar V$
. We claim that $\bar V$![]() satisfies also condition $(ii)$
satisfies also condition $(ii)$![]() in definition 1.2. For this we shall prove that for any fixed unit vector $\xi \in \bar V$
in definition 1.2. For this we shall prove that for any fixed unit vector $\xi \in \bar V$![]() , then
, then
Let $\xi \in \bar V$![]() be such that $|\xi |=1$
be such that $|\xi |=1$![]() and let
and let

Note that $v(n)\in V=V(n)$![]() and that
and that
Hence, for any $n$![]() sufficiently large, $|v(n)|>0$
sufficiently large, $|v(n)|>0$![]() . Using (3.2) with $\xi (n)=\frac {v(n)}{|v(n)|}\in V$
. Using (3.2) with $\xi (n)=\frac {v(n)}{|v(n)|}\in V$![]() we have
we have

Passing to the limit in the above inequality as $n\to +\infty$![]() and using Fatou's Lemma, $u\in LSC(\mathbb {R}^N)$
and using Fatou's Lemma, $u\in LSC(\mathbb {R}^N)$![]() and (3.4) we obtain
and (3.4) we obtain

The assumption $u\geq 0$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() yields $u(x_0+\tau \xi )=0$
yields $u(x_0+\tau \xi )=0$![]() for any $\tau \in \mathbb {R}$
for any $\tau \in \mathbb {R}$![]() . Thus, (3.3) holds.
. Thus, (3.3) holds.
The proofs of the following three theorems can be obtained, with minor changes, as those of theorems 2.3, 2.5 and 2.7, see also remark 2.6.
Theorem 3.3 Assume that $U$![]() is an open set satisfying ${\mathcal {G}}_{\Omega,U,k}$
is an open set satisfying ${\mathcal {G}}_{\Omega,U,k}$![]() . Then there exists a nonnegative and bounded (in $\mathbb {R}^N$
. Then there exists a nonnegative and bounded (in $\mathbb {R}^N$![]() ) supersolution $u\in LSC(\mathbb {R}^N)$
) supersolution $u\in LSC(\mathbb {R}^N)$![]() of
of
such that
Theorem 3.4 Assume that $U$![]() is an open subset of $\mathbb {R}^N$
is an open subset of $\mathbb {R}^N$![]() that satisfies ${\mathcal {G}}_{\mathbb {R}^N,U,k}$
that satisfies ${\mathcal {G}}_{\mathbb {R}^N,U,k}$![]() . Then there exists a nonnegative and bounded viscosity supersolution $u\in \mathrm {Lip}(\mathbb {R}^N)$
. Then there exists a nonnegative and bounded viscosity supersolution $u\in \mathrm {Lip}(\mathbb {R}^N)$![]() of
of
such that $U=\left \{x\in \mathbb {R}^N\,:\;u(x)>0\right \}$![]() .
.
Theorem 3.5 Let $U$![]() be an open set verifying ${\mathcal {G}}_{\Omega,U,k}$
be an open set verifying ${\mathcal {G}}_{\Omega,U,k}$![]() and assume that $\Omega \cap \partial U$
and assume that $\Omega \cap \partial U$![]() is a smooth hypersurface. Then
is a smooth hypersurface. Then
The geometric condition ${\mathcal {G}}_{\mathbb {R}^N,U,N-1}$![]() implies the convexity of any connected component of $U$
implies the convexity of any connected component of $U$![]() , as shown in the next
, as shown in the next
Theorem 3.6 Let $U\subset \mathbb {R}^N$![]() be open set satisfying condition ${\mathcal {G}}_{\mathbb {R}^N,U,N-1}$
be open set satisfying condition ${\mathcal {G}}_{\mathbb {R}^N,U,N-1}$![]() . Then any connected component of $U$
. Then any connected component of $U$![]() is a convex set.
is a convex set.
Proof. Let $U_0$![]() be a connected component of $U$
be a connected component of $U$![]() . Note that $U_0$
. Note that $U_0$![]() is an open subset of $U$
is an open subset of $U$![]() since $U$
since $U$![]() is locally connected.
is locally connected.
To the contrary that $U_0$![]() is a convex set, we suppose that $U_0$
is a convex set, we suppose that $U_0$![]() is not convex, which implies that there are two distinct points $x,y\in U_0$
is not convex, which implies that there are two distinct points $x,y\in U_0$![]() such that the line segment $[x,y]:=\{tx+(1-t)y : t\in [0,1]\}$
such that the line segment $[x,y]:=\{tx+(1-t)y : t\in [0,1]\}$![]() is not contained in $U_0$
is not contained in $U_0$![]() . This implies that $[x,y]$
. This implies that $[x,y]$![]() is not contained in $U$
is not contained in $U$![]() . Indeed, if we suppose that $[x,y]\subset U$
. Indeed, if we suppose that $[x,y]\subset U$![]() , then $[x,y]$
, then $[x,y]$![]() is a connected subset of $U$
is a connected subset of $U$![]() and intersects $U_0$
and intersects $U_0$![]() , and therefore, $U_0\cup [x,y]$
, and therefore, $U_0\cup [x,y]$![]() is a connected subset of $U$
is a connected subset of $U$![]() , which yields a contradiction that $[x,y]\subset U_0$
, which yields a contradiction that $[x,y]\subset U_0$![]() . Thus, we find that $[x,y]$
. Thus, we find that $[x,y]$![]() is not contained in $U$
is not contained in $U$![]() . We can choose $\lambda \in (0,1)$
. We can choose $\lambda \in (0,1)$![]() so that $z:=\lambda x+(1-\lambda )y\not \in U$
so that $z:=\lambda x+(1-\lambda )y\not \in U$![]() . By the property ${\mathcal {G}}_{\mathbb {R}^N,U,N-1}$
. By the property ${\mathcal {G}}_{\mathbb {R}^N,U,N-1}$![]() , we can choose $(N-1)$
, we can choose $(N-1)$![]() -dimensional linear subspace $V$
-dimensional linear subspace $V$![]() of $\mathbb {R}^N$
of $\mathbb {R}^N$![]() such that $(z+V)\cap U=\emptyset$
such that $(z+V)\cap U=\emptyset$![]() . Select $\nu \in \mathbb {R}^N\setminus \{0\}$
. Select $\nu \in \mathbb {R}^N\setminus \{0\}$![]() so that $z+V=\{p\in \mathbb {R}^N : \langle \nu, p-z\rangle =0\}$
so that $z+V=\{p\in \mathbb {R}^N : \langle \nu, p-z\rangle =0\}$![]() and set
and set
Observe that
that the right-hand side of (3.5) is a disjoint union of two open subsets of $U$![]() , and that either $x\in H^+$
, and that either $x\in H^+$![]() and $y\in H^-$
and $y\in H^-$![]() , or $x\in H^-$
, or $x\in H^-$![]() and $y\in H^+$
and $y\in H^+$![]() , which assures that both $H^+\cap U_0$
, which assures that both $H^+\cap U_0$![]() and $H^-\cap U_0$
and $H^-\cap U_0$![]() are nonempty. Hence, (3.5) contradicts the connectedness of $U_0$
are nonempty. Hence, (3.5) contradicts the connectedness of $U_0$![]() , which completes the proof.
, which completes the proof.
As a consequence of theorems 3.2 and 3.6, we have the following,
Theorem 3.7 Let $u\in LSC(\mathbb {R}^N)$![]() be a bounded and nonnegative supersolution of
be a bounded and nonnegative supersolution of
and satisfy $\min_{\mathbb R^N}u=0$![]() . Then any connected components of its positivity set is a convex set.
. Then any connected components of its positivity set is a convex set.
Remark 3.8 Theorem 3.7 is not true for supersolutions of
when $k< N-1$![]() and $N\geq 3$
and $N\geq 3$![]() . As an example consider
. As an example consider
Then $U$![]() has the property ${\mathcal {G}}_{\mathbb {R}^N,U,k}$
has the property ${\mathcal {G}}_{\mathbb {R}^N,U,k}$![]() for any $k\leq N-2$
for any $k\leq N-2$![]() . For this it is sufficient to consider any $k$
. For this it is sufficient to consider any $k$![]() -dimensional linear space $V\subseteq \left \{(0,0,x_3,\ldots,x_N)\right \}$
-dimensional linear space $V\subseteq \left \{(0,0,x_3,\ldots,x_N)\right \}$![]() in order to fulfil condition $(ii)$
in order to fulfil condition $(ii)$![]() of definition 1.2.
of definition 1.2.
By theorem 3.3, or theorem 3.4, there exists a bounded and nonnegative viscosity supersolution of (3.7) whose positivity set coincides with $U$![]() . On the other hand, it is clear that $U$
. On the other hand, it is clear that $U$![]() is not convex.
is not convex.
Acknowledgements
I.B. and G.G were partially supported by INdAM-GNAMPA.
Part of this work was done while H.I. was visiting the Dipartimento di Matematica, Sapienza Università di Roma in April–May, 2022. H.I. acknowledges the department for its hospitality and financial support. He was also partially supported by the JSPS grants KAKENHI nos. 20K03688, 20H01817, and 21H00717.