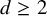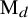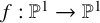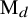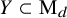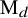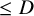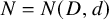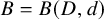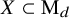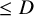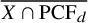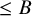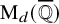1 Introduction
For each integer
![]() $d\geq 2$
, let
$d\geq 2$
, let
![]() $\mathrm {M}_d$
denote the moduli space of maps
$\mathrm {M}_d$
denote the moduli space of maps
![]() $f: \mathbb {P}^1\to \mathbb {P}^1$
of degree d, defined over the field
$f: \mathbb {P}^1\to \mathbb {P}^1$
of degree d, defined over the field
![]() $\mathbb {C}$
of complex numbers. The space
$\mathbb {C}$
of complex numbers. The space
![]() $\mathrm {M}_d$
consists of Möbius conjugacy classes of maps f; it is constructed as a complex orbifold in [Reference MilnorMi1] and as a scheme over
$\mathrm {M}_d$
consists of Möbius conjugacy classes of maps f; it is constructed as a complex orbifold in [Reference MilnorMi1] and as a scheme over
![]() $\operatorname {Spec} \mathbb {Z}$
in [Reference SilvermanSi1]. Let
$\operatorname {Spec} \mathbb {Z}$
in [Reference SilvermanSi1]. Let
![]() $\mathrm {PCF}_d\subset \mathrm {M}_d$
denote the subset of postcritically finite maps; that is, the conjugacy classes of maps f for which each critical point has a finite forward orbit. We say that an irreducible complex algebraic subvariety
$\mathrm {PCF}_d\subset \mathrm {M}_d$
denote the subset of postcritically finite maps; that is, the conjugacy classes of maps f for which each critical point has a finite forward orbit. We say that an irreducible complex algebraic subvariety
![]() $X \subset \mathrm {M}_d$
is PCF-special if
$X \subset \mathrm {M}_d$
is PCF-special if
![]() $\mathrm {PCF}_d\cap X$
is Zariski dense in X. Note that
$\mathrm {PCF}_d\cap X$
is Zariski dense in X. Note that
![]() $\mathrm {M}_d$
is itself PCF-special, as is the polynomial subvariety
$\mathrm {M}_d$
is itself PCF-special, as is the polynomial subvariety
![]() $\mathrm {MPoly}_d \subset \mathrm {M}_d$
, as are all subvarieties defined by orbit relations among the critical points; see, for example, [Reference Baker and DeMarcoBD, Proposition 2.6] and [Reference DeMarcoDe2, Theorem 6.2]. Conjecturally, all PCF-special subvarieties are determined by critical orbit relations (in a general sense, accounting for symmetries among the maps) [Reference Baker and DeMarcoBD, Conjecture 1.10].
$\mathrm {MPoly}_d \subset \mathrm {M}_d$
, as are all subvarieties defined by orbit relations among the critical points; see, for example, [Reference Baker and DeMarcoBD, Proposition 2.6] and [Reference DeMarcoDe2, Theorem 6.2]. Conjecturally, all PCF-special subvarieties are determined by critical orbit relations (in a general sense, accounting for symmetries among the maps) [Reference Baker and DeMarcoBD, Conjecture 1.10].
In this article, we study the geometry of the set
![]() $\mathrm {PCF}_d$
by examining how it intersects with families of varieties in
$\mathrm {PCF}_d$
by examining how it intersects with families of varieties in
![]() $\mathrm {M}_d$
, and we prove uniform bounds on the degrees of PCF-special subvarieties in these families. Here, and throughout this article, we measure degree with respect to a fixed choice of very ample line bundle on
$\mathrm {M}_d$
, and we prove uniform bounds on the degrees of PCF-special subvarieties in these families. Here, and throughout this article, we measure degree with respect to a fixed choice of very ample line bundle on
![]() $\mathrm {M}_d$
, for example providing the projective compactification of
$\mathrm {M}_d$
, for example providing the projective compactification of
![]() $\mathrm {M}_d$
defined in [Reference SilvermanSi1]. The degree bounds will depend on the choice, but the following result holds for any such choice:
$\mathrm {M}_d$
defined in [Reference SilvermanSi1]. The degree bounds will depend on the choice, but the following result holds for any such choice:
Theorem 1.1. Fix integers
![]() $d\geq 2$
and
$d\geq 2$
and
![]() $D\geq 1$
. There exist constants
$D\geq 1$
. There exist constants
![]() $B = B(D,d)$
and
$B = B(D,d)$
and
![]() $N = N(D,d)$
so that for any complex algebraic subvariety
$N = N(D,d)$
so that for any complex algebraic subvariety
![]() $X \subset \mathrm {M}_d$
of degree
$X \subset \mathrm {M}_d$
of degree
![]() $\leq D$
, the Zariski closure
$\leq D$
, the Zariski closure
has at most N irreducible components, each with degree
![]() $\leq B$
.
$\leq B$
.
Theorem 1.2. Fix integers
![]() $d\geq 2$
and
$d\geq 2$
and
![]() $D \geq 1$
. There are only finitely many positive-dimensional irreducible PCF-special subvarieties in
$D \geq 1$
. There are only finitely many positive-dimensional irreducible PCF-special subvarieties in
![]() $\mathrm {M}_d$
with degree
$\mathrm {M}_d$
with degree
![]() $\leq D$
.
$\leq D$
.
Example 1.3. Consider the sequence of PCF-special curves
![]() $\mathrm {Per}_n(0)$
in
$\mathrm {Per}_n(0)$
in
![]() $\mathrm {M}_2$
, defined by the condition that one critical point of a quadratic rational map has exact period n. These were introduced by Milnor in [Reference MilnorMi1] and conjectured to be irreducible for every n. While irreducibility remains open, Theorem 1.2 implies that the degrees of the irreducible components of
$\mathrm {M}_2$
, defined by the condition that one critical point of a quadratic rational map has exact period n. These were introduced by Milnor in [Reference MilnorMi1] and conjectured to be irreducible for every n. While irreducibility remains open, Theorem 1.2 implies that the degrees of the irreducible components of
![]() $\mathrm {Per}_n(0)$
must be growing with n. Theorem 1.2 implies degree growth also of the irreducible components of the analogous hypersurfaces
$\mathrm {Per}_n(0)$
must be growing with n. Theorem 1.2 implies degree growth also of the irreducible components of the analogous hypersurfaces
![]() $\mathrm {Per}_n(0)$
in
$\mathrm {Per}_n(0)$
in
![]() $\mathrm {M}_d$
, for every
$\mathrm {M}_d$
, for every
![]() $d\geq 2$
.
$d\geq 2$
.
Example 1.4. Consider the family of curves
![]() $\mathrm {Per}_1(\lambda )$
in
$\mathrm {Per}_1(\lambda )$
in
![]() $\mathrm {M}_2$
, parameterized by
$\mathrm {M}_2$
, parameterized by
![]() $\lambda \in \mathbb {C}$
, consisting of all quadratic maps having a fixed point of multiplier
$\lambda \in \mathbb {C}$
, consisting of all quadratic maps having a fixed point of multiplier
![]() $\lambda $
. This family was first introduced by Milnor in [Reference MilnorMi1], and they are lines in the natural coordinates that Milnor introduced on
$\lambda $
. This family was first introduced by Milnor in [Reference MilnorMi1], and they are lines in the natural coordinates that Milnor introduced on
![]() $\mathrm {M}_2 \simeq \mathbb {C}^2$
. It is known that
$\mathrm {M}_2 \simeq \mathbb {C}^2$
. It is known that
![]() $\mathrm {Per}_1(\lambda )$
is PCF-special if and only if
$\mathrm {Per}_1(\lambda )$
is PCF-special if and only if
![]() $\lambda = 0$
[Reference DeMarco, Wang and YeDWY]. And although
$\lambda = 0$
[Reference DeMarco, Wang and YeDWY]. And although
![]() $\mathrm {PCF}_d$
is Zariski-dense in
$\mathrm {PCF}_d$
is Zariski-dense in
![]() $\mathrm {M}_2$
, Theorem 1.1 combined with the main result of [Reference DeMarco, Wang and YeDWY] implies: There is a uniform bound N so that
$\mathrm {M}_2$
, Theorem 1.1 combined with the main result of [Reference DeMarco, Wang and YeDWY] implies: There is a uniform bound N so that
for all
![]() $\lambda \not = 0$
in
$\lambda \not = 0$
in
![]() $\mathbb {C}$
. Theorem 1.1 also implies the corresponding result for the family of curves
$\mathbb {C}$
. Theorem 1.1 also implies the corresponding result for the family of curves
![]() $\mathrm {Per}_n(\lambda )$
in the moduli space
$\mathrm {Per}_n(\lambda )$
in the moduli space
![]() $\mathrm {MPoly}_3$
of cubic polynomials, for any fixed
$\mathrm {MPoly}_3$
of cubic polynomials, for any fixed
![]() $n\geq 1$
, in view of [Reference Baker and DeMarcoBD, Theorem 1.1] [Reference Favre and GauthierFG2, Theorem B].
$n\geq 1$
, in view of [Reference Baker and DeMarcoBD, Theorem 1.1] [Reference Favre and GauthierFG2, Theorem B].
In fact we prove stronger versions of Theorem 1.1 and Theorem 1.2 in the spirit of the Bogomolov Conjecture [Reference UllmoUl, Reference ZhangZh1] or, more recently, of the “height gap principle” [Reference Gao, Ge and KühneGGK, Reference GaoGao] in the setting of abelian varieties, for subvarieties of
![]() $\mathrm {M}_d$
defined over
$\mathrm {M}_d$
defined over
![]() $\overline {\mathbb {Q}}$
. The critical height of a conjugacy class
$\overline {\mathbb {Q}}$
. The critical height of a conjugacy class
![]() $[f]\in \mathrm {M}_d(\overline {\mathbb {Q}})$
is defined by
$[f]\in \mathrm {M}_d(\overline {\mathbb {Q}})$
is defined by
 $$ \begin{align*}\hat{h}_{\mathrm{crit}}(f)=\sum_{\{c~:~f'(c)=0\}}\hat{h}_f(c) \; \ge \; 0,\end{align*} $$
$$ \begin{align*}\hat{h}_{\mathrm{crit}}(f)=\sum_{\{c~:~f'(c)=0\}}\hat{h}_f(c) \; \ge \; 0,\end{align*} $$
for any representative f defined over
![]() $\overline {\mathbb {Q}}$
, where the critical points are counted with multiplicity and
$\overline {\mathbb {Q}}$
, where the critical points are counted with multiplicity and
![]() $\hat {h}_f$
is the Call-Silverman canonical height on
$\hat {h}_f$
is the Call-Silverman canonical height on
![]() $\mathbb {P}^1(\overline {\mathbb {Q}})$
[Reference Call and SilvermanCS] [Reference SilvermanSi2]. Ingram proved that
$\mathbb {P}^1(\overline {\mathbb {Q}})$
[Reference Call and SilvermanCS] [Reference SilvermanSi2]. Ingram proved that
![]() $\hat {h}_{\mathrm {crit}}$
is comparable to a Weil height on the open subset
$\hat {h}_{\mathrm {crit}}$
is comparable to a Weil height on the open subset
![]() $\mathrm {M}_d \setminus \mathcal {L}_d$
where
$\mathrm {M}_d \setminus \mathcal {L}_d$
where
![]() $\mathcal {L}_d$
is the locus of flexible Lattès maps [Reference IngramIn]. A more explicit version of Ingram’s result was later established in [Reference Gauthier, Okuyama and VignyGOV, Theorem C]. A different approach is given by the Yuan–Zhang theory of adelic line bundles; see [Reference Yuan and ZhangYZ, Remark 6.3.3]. The PCF points in
$\mathcal {L}_d$
is the locus of flexible Lattès maps [Reference IngramIn]. A more explicit version of Ingram’s result was later established in [Reference Gauthier, Okuyama and VignyGOV, Theorem C]. A different approach is given by the Yuan–Zhang theory of adelic line bundles; see [Reference Yuan and ZhangYZ, Remark 6.3.3]. The PCF points in
![]() $\mathrm {M}_d(\overline {\mathbb {Q}})$
are precisely those with
$\mathrm {M}_d(\overline {\mathbb {Q}})$
are precisely those with
![]() $\hat {h}_{\mathrm {crit}}(f) = 0$
.
$\hat {h}_{\mathrm {crit}}(f) = 0$
.
To state our results, we fix a projective embedding of
![]() $\mathrm {M}_d$
defined over
$\mathrm {M}_d$
defined over
![]() $\mathbb {Q}$
. We also fix height functions
$\mathbb {Q}$
. We also fix height functions
![]() $h_{\mathrm {Ch}}$
on the associated Chow varieties
$h_{\mathrm {Ch}}$
on the associated Chow varieties
![]() $\mathrm {Ch}(\mathrm {M}_d, r, D)$
of cycles of dimension r and degree
$\mathrm {Ch}(\mathrm {M}_d, r, D)$
of cycles of dimension r and degree
![]() $\leq D$
in
$\leq D$
in
![]() $\mathrm {M}_d$
, for example, a Philippon height [Reference PhilipponPh]; see §2.5 for definitions. The constants B, N, and
$\mathrm {M}_d$
, for example, a Philippon height [Reference PhilipponPh]; see §2.5 for definitions. The constants B, N, and
![]() $\epsilon $
of the following theorems will depend on these choices.
$\epsilon $
of the following theorems will depend on these choices.
Theorem 1.5. Fix integers
![]() $d\geq 2$
and
$d\geq 2$
and
![]() $D\geq 1$
. There exist constants
$D\geq 1$
. There exist constants
![]() $B = B(D,d)$
,
$B = B(D,d)$
,
![]() $N= N(D,d)$
, and
$N= N(D,d)$
, and
![]() $\epsilon =\epsilon (D,d)>0$
so that for any irreducible algebraic subvariety
$\epsilon =\epsilon (D,d)>0$
so that for any irreducible algebraic subvariety
![]() $X \subset \mathrm {M}_d$
of degree
$X \subset \mathrm {M}_d$
of degree
![]() $\leq D$
defined over
$\leq D$
defined over
![]() $\overline {\mathbb {Q}}$
, and every
$\overline {\mathbb {Q}}$
, and every
![]() $0\le \epsilon '<\epsilon $
, the Zariski closure
$0\le \epsilon '<\epsilon $
, the Zariski closure
has at most N irreducible components, each with degree
![]() $\leq B$
.
$\leq B$
.
The essential minimum of the critical height on a subvariety
![]() $Y\subset \mathrm {M}_d$
defined over
$Y\subset \mathrm {M}_d$
defined over
![]() $\overline {\mathbb {Q}}$
is
$\overline {\mathbb {Q}}$
is
where the supremum is taken over all proper subvarieties
![]() $Y'$
in Y defined over
$Y'$
in Y defined over
![]() $\overline {\mathbb {Q}}$
. Note that all PCF-special subvarieties
$\overline {\mathbb {Q}}$
. Note that all PCF-special subvarieties
![]() $Y\subset \mathrm {M}_d$
are defined over
$Y\subset \mathrm {M}_d$
are defined over
![]() $\overline {\mathbb {Q}}$
and have essential minimum 0, because they contain a Zariski-dense set of PCF points that can be defined over
$\overline {\mathbb {Q}}$
and have essential minimum 0, because they contain a Zariski-dense set of PCF points that can be defined over
![]() $\overline {\mathbb {Q}}$
; see §2.2. We also prove the following result, strengthening Theorem 1.2.
$\overline {\mathbb {Q}}$
; see §2.2. We also prove the following result, strengthening Theorem 1.2.
Theorem 1.6. Fix integers
![]() $d\geq 2$
and
$d\geq 2$
and
![]() $D \geq 1$
. There exists
$D \geq 1$
. There exists
![]() $\epsilon "=\epsilon "(d,D)> 0$
such that there are only finitely many positive-dimensional irreducible subvarieties
$\epsilon "=\epsilon "(d,D)> 0$
such that there are only finitely many positive-dimensional irreducible subvarieties
![]() $Y\subset \mathrm {M}_d$
defined over
$Y\subset \mathrm {M}_d$
defined over
![]() $\overline {\mathbb {Q}}$
with degree
$\overline {\mathbb {Q}}$
with degree
![]() $\leq D$
and
$\leq D$
and
![]() $\mathrm {ess.min.}(\hat {h}_{\mathrm {crit}}|_Y) \leq \epsilon "\max \{1,h_{\mathrm {Ch}}(Y)\}.$
$\mathrm {ess.min.}(\hat {h}_{\mathrm {crit}}|_Y) \leq \epsilon "\max \{1,h_{\mathrm {Ch}}(Y)\}.$
1.1 History and context
The study of the PCF-special varieties in
![]() $\mathrm {M}_d$
grew out of parallels between the theory of complex dynamical systems and the study of abelian varieties. A conjectural classification of PCF-special subvarieties in
$\mathrm {M}_d$
grew out of parallels between the theory of complex dynamical systems and the study of abelian varieties. A conjectural classification of PCF-special subvarieties in
![]() $\mathrm {M}_d$
first appears in [Reference SilvermanSi2, Chapter 6] where it was given the name of “Dynamical André-Oort” (or “DAO” as it is known in [Reference Ji and XieJX]), because the geometry of the PCF locus in
$\mathrm {M}_d$
first appears in [Reference SilvermanSi2, Chapter 6] where it was given the name of “Dynamical André-Oort” (or “DAO” as it is known in [Reference Ji and XieJX]), because the geometry of the PCF locus in
![]() $\mathrm {M}_d$
shares features with the locus of CM points in a moduli space of abelian varieties; see [Reference ZannierZa] for background on several Unlikely Intersection problems. The first cases of DAO were proved by Baker-DeMarco [Reference Baker and DeMarcoBD] and Ghioca-Hsia-Tucker [Reference Ghioca, Hsia and TuckerGHT], followed by a series of results mostly focused on polynomial dynamics where the relations and symmetries are understood, such as [Reference Ghioca and YeGY, Reference Favre and GauthierFG2], culminating in a complete classification of PCF-special curves in moduli spaces of polynomials by Favre-Gauthier [Reference Favre and GauthierFG3] and a characterization of PCF-special curves in
$\mathrm {M}_d$
shares features with the locus of CM points in a moduli space of abelian varieties; see [Reference ZannierZa] for background on several Unlikely Intersection problems. The first cases of DAO were proved by Baker-DeMarco [Reference Baker and DeMarcoBD] and Ghioca-Hsia-Tucker [Reference Ghioca, Hsia and TuckerGHT], followed by a series of results mostly focused on polynomial dynamics where the relations and symmetries are understood, such as [Reference Ghioca and YeGY, Reference Favre and GauthierFG2], culminating in a complete classification of PCF-special curves in moduli spaces of polynomials by Favre-Gauthier [Reference Favre and GauthierFG3] and a characterization of PCF-special curves in
![]() $\mathrm {M}_d$
by Ji-Xie [Reference Ji and XieJX]. We note, however, that there are currently no known classification results for PCF-special subvarieties of dimensions
$\mathrm {M}_d$
by Ji-Xie [Reference Ji and XieJX]. We note, however, that there are currently no known classification results for PCF-special subvarieties of dimensions
![]() $> 1$
, even when restricting to spaces of polynomials. Nevertheless, Theorem 1.1 can be viewed as a “Uniform DAO” that holds for PCF-special subvarieties of any dimension.
$> 1$
, even when restricting to spaces of polynomials. Nevertheless, Theorem 1.1 can be viewed as a “Uniform DAO” that holds for PCF-special subvarieties of any dimension.
The questions addressed here are inspired by Pink’s conjectures [Reference PinkPi] in the setting of families of abelian varieties, and the uniformity results about subgroup schemes in families of abelian varieties, for example, as obtained recently in [Reference KühneKü, Reference Dimitrov, Gao and HabeggerDGH, Reference Gao, Ge and KühneGGK, Reference Gao and HabeggerGH, Reference YuanYu]. The analogous study of preperiodic subvarieties for regular self-maps of projective spaces (or more generally, for polarized dynamical systems, which then includes the geometry of subgroups in abelian varieties) was initiated by Zhang (see, for example, [Reference ZhangZh2]). Uniform bounds on the geometry of preperiodic points appeared in [Reference DeMarco, Krieger and YeDKY1, Reference DeMarco, Krieger and YeDKY2, Reference DeMarco and Myrto MavrakiDM2, Reference Myrto Mavraki and SchmidtMaS].
Remark 1.7. We emphasize that the aforementioned uniformity results each relied crucially on the classification of the “special” varieties in their respective settings. In contrast, the classification of PCF-special subvarieties is only conjectural [Reference Baker and DeMarcoBD]; we obtain uniformity without proving that PCF-special subvarieties are necessarily defined by critical orbit relations. In particular, we do not recover (or use) the main result of [Reference Ji and XieJX] for curves in
![]() $\mathrm {M}_d$
, and each of our theorems is new also for curves in
$\mathrm {M}_d$
, and each of our theorems is new also for curves in
![]() $\mathrm {M}_d$
. We do not know of any other result in the literature where uniformity is known without the classification.
$\mathrm {M}_d$
. We do not know of any other result in the literature where uniformity is known without the classification.
A far-reaching conjecture in [Reference DeMarco and MavrakiDM3] implies the classification of PCF-special subvarieties (as formulated in [Reference Baker and DeMarcoBD, Conjecture 1.10]) and the uniform bounds on their geometry (our Theorems 1.1 and 1.2) and many results about geometry of torsion points in abelian varieties as special cases. It also contains the (partial) uniformity results obtained in [Reference DeMarco and MavrakiDM1] and [Reference Gauthier, Taflin and VignyGTV].
Finally, we remark that we do not give explicit bounds on B and N in Theorem 1.1, nor on the number of PCF-special subvarieties in Theorem 1.2. It would be very interesting to know how large these values must be and how they depend on d and D (and the dimension of the PCF-special subvarieties). In different contexts, some effective bounds have been given in [Reference DeMarco, Krieger and YeDKY2, Reference David and PhilipponDP, Reference DeMarco and Myrto MavrakiDM2].
1.2 Proof strategy
We build upon the theory of arithmetic equidistribution for heights on quasiprojective varieties [Reference KühneKü, Reference GauthierGa3, Reference Yuan and ZhangYZ], and we make use of complex-dynamical tools for analyzing bifurcation measures as in [Reference Buff and EpsteinBE, Reference DujardinDu].
We consider families
![]() $\mathcal {X}\to V$
of r-dimensional varieties
$\mathcal {X}\to V$
of r-dimensional varieties
![]() $X_{\lambda }\subset \mathrm {M}_d$
, parametrized by
$X_{\lambda }\subset \mathrm {M}_d$
, parametrized by
![]() $\lambda $
in an irreducible quasi-projective variety V of dimension
$\lambda $
in an irreducible quasi-projective variety V of dimension
![]() $\ell \ge 1$
. We say that a family
$\ell \ge 1$
. We say that a family
![]() $\mathcal {X}\to V$
is maximally varying if the natural map from V to the Chow variety
$\mathcal {X}\to V$
is maximally varying if the natural map from V to the Chow variety
![]() $\mathrm {Ch}(\mathrm {M}_d, r, D)$
has finite fibers, where
$\mathrm {Ch}(\mathrm {M}_d, r, D)$
has finite fibers, where
![]() $\mathrm {Ch}(\mathrm {M}_d, r, D)$
is a space of cycles of
$\mathrm {Ch}(\mathrm {M}_d, r, D)$
is a space of cycles of
![]() $\mathrm {M}_d$
with dimension r and degree
$\mathrm {M}_d$
with dimension r and degree
![]() $\leq D$
, with respect to a fixed projective embedding of
$\leq D$
, with respect to a fixed projective embedding of
![]() $\mathrm {M}_d$
defined over
$\mathrm {M}_d$
defined over
![]() $\mathbb {Q}$
; see §2.5.
$\mathbb {Q}$
; see §2.5.
For any positive integer m, we let
![]() $\mathcal {X}_V^m$
denote the m-th fiber power of
$\mathcal {X}_V^m$
denote the m-th fiber power of
![]() $\mathcal {X}$
over V. We denote elements of
$\mathcal {X}$
over V. We denote elements of
![]() $\mathcal {X}_V^{m}$
by
$\mathcal {X}_V^{m}$
by
![]() $(\lambda , f_1, \ldots , f_m)$
, with
$(\lambda , f_1, \ldots , f_m)$
, with
![]() $f_i \in X_\lambda $
for each i. Our main theorems are derived from the following result, which is inspired from the Relative Bogomolov Conjecture [Reference Dimitrov, Gao and HabeggerDGH2] and by results in [Reference KühneKü] and [Reference Gao, Ge and KühneGGK].
$f_i \in X_\lambda $
for each i. Our main theorems are derived from the following result, which is inspired from the Relative Bogomolov Conjecture [Reference Dimitrov, Gao and HabeggerDGH2] and by results in [Reference KühneKü] and [Reference Gao, Ge and KühneGGK].
Theorem 1.8. Let
![]() $\mathcal {X}\to V$
be a maximally varying family of dimension
$\mathcal {X}\to V$
be a maximally varying family of dimension
![]() $r\ge 1$
varieties in
$r\ge 1$
varieties in
![]() $\mathrm {M}_d$
, parametrized by an irreducible quasi-projective variety V of dimension
$\mathrm {M}_d$
, parametrized by an irreducible quasi-projective variety V of dimension
![]() $\ell \ge 1$
, all defined over
$\ell \ge 1$
, all defined over
![]() $\overline {\mathbb {Q}}$
. Assume that the generic fiber of
$\overline {\mathbb {Q}}$
. Assume that the generic fiber of
![]() $\mathcal {X}\to V$
is geometrically irreducible. There exists
$\mathcal {X}\to V$
is geometrically irreducible. There exists
![]() $\epsilon =\epsilon (\mathcal {X})>0$
such that the set
$\epsilon =\epsilon (\mathcal {X})>0$
such that the set
 $$ \begin{align*}Z_\varepsilon(\mathcal{X}) := \left\{(\lambda,f_1,\ldots,f_{\ell+1})\in \mathcal{X}_V^{\ell+1}(\overline{\mathbb{Q}})~:~ \sum_{i=1}^{\ell+1}\hat{h}_{\mathrm{crit}}(f_i)<\epsilon \max\{1,h_{\mathrm{Ch}}(\lambda)\}\right\}\end{align*} $$
$$ \begin{align*}Z_\varepsilon(\mathcal{X}) := \left\{(\lambda,f_1,\ldots,f_{\ell+1})\in \mathcal{X}_V^{\ell+1}(\overline{\mathbb{Q}})~:~ \sum_{i=1}^{\ell+1}\hat{h}_{\mathrm{crit}}(f_i)<\epsilon \max\{1,h_{\mathrm{Ch}}(\lambda)\}\right\}\end{align*} $$
is not Zariski dense in
![]() $\mathcal {X}_V^{\ell +1}$
.
$\mathcal {X}_V^{\ell +1}$
.
To prove Theorem 1.8, we first pass to a maximally varying family of varieties
![]() $\mathcal {X}' \to V$
in a finite branched cover
$\mathcal {X}' \to V$
in a finite branched cover
![]() $\mathcal {M}_d^{cm} \to \mathrm {M}_d$
that parameterizes maps on
$\mathcal {M}_d^{cm} \to \mathrm {M}_d$
that parameterizes maps on
![]() $\mathbb {P}^1$
with marked critical points
$\mathbb {P}^1$
with marked critical points
![]() $c_1, \ldots , c_{2d-2}: \mathcal {M}_d^{cm} \to \mathbb {P}^1$
. We construct two nonzero bifurcation measures on the fiber power
$c_1, \ldots , c_{2d-2}: \mathcal {M}_d^{cm} \to \mathbb {P}^1$
. We construct two nonzero bifurcation measures on the fiber power
![]() $(\mathcal {X}')_V^{\ell +1}$
, from two distinct r-tuples of critical points, and, associated to these measures, we define two adelically metrized line bundles on the quasiprojective
$(\mathcal {X}')_V^{\ell +1}$
, from two distinct r-tuples of critical points, and, associated to these measures, we define two adelically metrized line bundles on the quasiprojective
![]() $(\mathcal {X}')_V^{\ell +1}$
, in the sense of [Reference Yuan and ZhangYZ]. The construction of the measures is carried out in Section 3, and their nonvanishing ultimately comes from properties of the bifurcation current and its powers in
$(\mathcal {X}')_V^{\ell +1}$
, in the sense of [Reference Yuan and ZhangYZ]. The construction of the measures is carried out in Section 3, and their nonvanishing ultimately comes from properties of the bifurcation current and its powers in
![]() $\mathrm {M}_d$
from [Reference McMullenMc1, Reference DeMarcoDe1, Reference DujardinDu, Reference Gauthier, Okuyama and VignyGOV]. The nonvanishing of the measures implies that the two metrized line bundles are non-degenerate (as defined in [Reference Yuan and ZhangYZ]). We are thus able to deduce from the height inequality of [Reference Yuan and ZhangYZ, Theorem 1.3.2] that, if
$\mathrm {M}_d$
from [Reference McMullenMc1, Reference DeMarcoDe1, Reference DujardinDu, Reference Gauthier, Okuyama and VignyGOV]. The nonvanishing of the measures implies that the two metrized line bundles are non-degenerate (as defined in [Reference Yuan and ZhangYZ]). We are thus able to deduce from the height inequality of [Reference Yuan and ZhangYZ, Theorem 1.3.2] that, if
![]() $\epsilon>0$
is sufficiently small, then “most” points of
$\epsilon>0$
is sufficiently small, then “most” points of
![]() $Z_\epsilon (\mathcal {X})$
lie in subvarieties
$Z_\epsilon (\mathcal {X})$
lie in subvarieties
![]() $X_\lambda $
of bounded
$X_\lambda $
of bounded
![]() $h_{\mathrm {Ch}}$
-height.
$h_{\mathrm {Ch}}$
-height.
We now proceed by contradiction: if no such
![]() $\epsilon $
exists, then there will be a generic sequence of points in
$\epsilon $
exists, then there will be a generic sequence of points in
![]() $(\mathcal {X}')_V^{\ell +1}(\overline {\mathbb {Q}})$
with
$(\mathcal {X}')_V^{\ell +1}(\overline {\mathbb {Q}})$
with
![]() $\sum _{i=1}^{\ell +1}\hat {h}_{\mathrm {crit}}(f_i)$
tending to 0. We apply [Reference Yuan and ZhangYZ, Theorem 5.4.3] to deduce that the Galois orbits of these points will be equidistributed with respect to the two bifurcation measures, implying the two measures coincide.
$\sum _{i=1}^{\ell +1}\hat {h}_{\mathrm {crit}}(f_i)$
tending to 0. We apply [Reference Yuan and ZhangYZ, Theorem 5.4.3] to deduce that the Galois orbits of these points will be equidistributed with respect to the two bifurcation measures, implying the two measures coincide.
The contradiction will come from an analysis of the two measures. More precisely, using a slicing argument as in [Reference Myrto Mavraki and SchmidtMaS] (which was revisited in [Reference DeMarco and MavrakiDM1]), it suffices to analyze the family of bifurcation measures they induce on the fibers
![]() $X_{\lambda }$
. Here we appeal to the maximal variation of the family and the dynamical theory of J-stability. We find a parameter
$X_{\lambda }$
. Here we appeal to the maximal variation of the family and the dynamical theory of J-stability. We find a parameter
![]() $\lambda _0 \in V$
and conjugacy class
$\lambda _0 \in V$
and conjugacy class
![]() $[f_0] \in X_{\lambda _0}$
so that one collection of r critical points is pre-repelling for
$[f_0] \in X_{\lambda _0}$
so that one collection of r critical points is pre-repelling for
![]() $f_0$
, while one of the critical points in the other r-tuple is in the basin of a parabolic point. We then zoom into the parameter space at
$f_0$
, while one of the critical points in the other r-tuple is in the basin of a parabolic point. We then zoom into the parameter space at
![]() $f_0$
, where the first r-tuple of preperiodic critical points yields an asymptotic similarity between the bifurcation measure and the dynamical space, exactly as in the proof of [Reference Buff and EpsteinBE, Main Theorem]. But zooming in at this rate yields 0 for the bifurcation measure defined with the second r-tuple of critical points, because one of the critical points has infinite orbit and is attracted to a parabolic cycle. Details are provided in Section 4. The proofs of Theorems 1.1, 1.2, 1.5, and 1.6 are completed in Section 5.
$f_0$
, where the first r-tuple of preperiodic critical points yields an asymptotic similarity between the bifurcation measure and the dynamical space, exactly as in the proof of [Reference Buff and EpsteinBE, Main Theorem]. But zooming in at this rate yields 0 for the bifurcation measure defined with the second r-tuple of critical points, because one of the critical points has infinite orbit and is attracted to a parabolic cycle. Details are provided in Section 4. The proofs of Theorems 1.1, 1.2, 1.5, and 1.6 are completed in Section 5.
1.3 Questions
Finally, we remark that our initial (failed) attempts to prove Theorems 1.8 were more in line with previously known cases of DAO, combined with the strategy from [Reference Myrto Mavraki and SchmidtMaS] to obtain uniform bounds, but we encountered several obstacles. We were led to the following questions, and we view each as a measure-theoretic strengthening of DAO.
Question 1.9. Suppose that
![]() $\Lambda $
is a complex manifold of dimension
$\Lambda $
is a complex manifold of dimension
![]() $r\ge 1$
, parameterizing a holomorphic family of maps
$r\ge 1$
, parameterizing a holomorphic family of maps
defined by
![]() $(\lambda , z) \mapsto (\lambda , f_\lambda (z))$
, and suppose that
$(\lambda , z) \mapsto (\lambda , f_\lambda (z))$
, and suppose that
![]() $c_1, \ldots , c_{r+1}: \Lambda \to \mathbb {P}^1$
are marked critical points of
$c_1, \ldots , c_{r+1}: \Lambda \to \mathbb {P}^1$
are marked critical points of
![]() $f_\lambda $
. Let
$f_\lambda $
. Let
![]() $T_i$
denote the bifurcation current on
$T_i$
denote the bifurcation current on
![]() $\Lambda $
associated to the pair
$\Lambda $
associated to the pair
![]() $(f, c_i)$
, defined in §2.3. Suppose that
$(f, c_i)$
, defined in §2.3. Suppose that
on
![]() $\Lambda $
for some
$\Lambda $
for some
![]() $\alpha>0$
. Can we conclude that the pair
$\alpha>0$
. Can we conclude that the pair
![]() $(c_r, c_{r+1})$
of critical points is dynamically related along
$(c_r, c_{r+1})$
of critical points is dynamically related along
![]() $\Lambda $
? In other words, does there exist a proper, complex-analytic subvariety
$\Lambda $
? In other words, does there exist a proper, complex-analytic subvariety
![]() $X \subset \Lambda \times (\mathbb {P}^1\times \mathbb {P}^1)$
which projects surjectively to
$X \subset \Lambda \times (\mathbb {P}^1\times \mathbb {P}^1)$
which projects surjectively to
![]() $\Lambda $
, is invariant for the action of
$\Lambda $
, is invariant for the action of
![]() $(f,f)$
, and contains the graph of
$(f,f)$
, and contains the graph of
![]() $(c_r, c_{r+1})$
over
$(c_r, c_{r+1})$
over
![]() $\Lambda $
?
$\Lambda $
?
The question has only been answered in a few special cases with
![]() $r=1$
: (1) for the 1-parameter families of polynomials treated by Baker-DeMarco in [Reference Baker and DeMarcoBD] parameterized by
$r=1$
: (1) for the 1-parameter families of polynomials treated by Baker-DeMarco in [Reference Baker and DeMarcoBD] parameterized by
![]() $\Lambda = \mathbb {C}$
, and (2) for the curves
$\Lambda = \mathbb {C}$
, and (2) for the curves
![]() $\Lambda = \mathrm {Per}_1(\eta )$
in
$\Lambda = \mathrm {Per}_1(\eta )$
in
![]() $\mathrm {M}_2$
, for each
$\mathrm {M}_2$
, for each
![]() $\eta \in \mathbb {C}$
, of Example 1.4 [Reference DeMarco, Wang and YeDWY].
$\eta \in \mathbb {C}$
, of Example 1.4 [Reference DeMarco, Wang and YeDWY].
Question 1.10. Suppose that
![]() $\Lambda $
is a smooth and irreducible, quasiprojective, complex algebraic variety of dimension
$\Lambda $
is a smooth and irreducible, quasiprojective, complex algebraic variety of dimension
![]() $r \geq 2$
and that
$r \geq 2$
and that
![]() $f: \Lambda \times \mathbb {P}^1 \to \Lambda \times \mathbb {P}^1$
is a morphism that defines an algebraic family of maps on
$f: \Lambda \times \mathbb {P}^1 \to \Lambda \times \mathbb {P}^1$
is a morphism that defines an algebraic family of maps on
![]() $\mathbb {P}^1$
, with marked critical points. With the notation of Question 1.9, suppose that
$\mathbb {P}^1$
, with marked critical points. With the notation of Question 1.9, suppose that
on
![]() $\Lambda $
but
$\Lambda $
but
on
![]() $\Lambda $
. Can we conclude that there exists
$\Lambda $
. Can we conclude that there exists
![]() $i \in \{1, \ldots , r-1\}$
so that the pair
$i \in \{1, \ldots , r-1\}$
so that the pair
![]() $(c_i, c_{r+1})$
is dynamically related along
$(c_i, c_{r+1})$
is dynamically related along
![]() $\Lambda $
? (We remark here that one can define a dynamical relation for a tuple
$\Lambda $
? (We remark here that one can define a dynamical relation for a tuple
![]() $(c_1,\ldots ,c_{r+1})$
as for a pair; see [Reference DeMarcoDe2, §6.2]. But it follows by [Reference Medvedev and ScanlonMeSc, Proposition 2.21] that dynamical relations always come in pairs.) We know of no cases of this question that have been answered.
$(c_1,\ldots ,c_{r+1})$
as for a pair; see [Reference DeMarcoDe2, §6.2]. But it follows by [Reference Medvedev and ScanlonMeSc, Proposition 2.21] that dynamical relations always come in pairs.) We know of no cases of this question that have been answered.
Remark 1.11. Versions of Theorems 1.1 and 1.2 are expected to hold in more general settings, for example when marking points on
![]() $\mathbb {P}^1$
are not necessarily critical, or upon working with preperiodic points in families of maps on
$\mathbb {P}^1$
are not necessarily critical, or upon working with preperiodic points in families of maps on
![]() $\mathbb {P}^N$
. See [Reference DeMarco and MavrakiDM3]. Analogues of Questions 1.9 and 1.10 can also be formulated, but we keep our focus in this article on the postcritically-finite maps on
$\mathbb {P}^N$
. See [Reference DeMarco and MavrakiDM3]. Analogues of Questions 1.9 and 1.10 can also be formulated, but we keep our focus in this article on the postcritically-finite maps on
![]() $\mathbb {P}^1$
and the bifurcation currents associated to marked critical points.
$\mathbb {P}^1$
and the bifurcation currents associated to marked critical points.
2 Background on
 $\mathrm {M}_d$
and its subvarieties
$\mathrm {M}_d$
and its subvarieties
In this section, we provide important background on the moduli spaces
![]() $\mathrm {M}_d$
, and we look into properties of a maximally varying family
$\mathrm {M}_d$
, and we look into properties of a maximally varying family
![]() $\mathcal {X} \to V$
of subvarieties of
$\mathcal {X} \to V$
of subvarieties of
![]() $\mathrm {M}_d$
.
$\mathrm {M}_d$
.
2.1 The moduli space
 $\mathrm {M}_d$
and a critically-marked parameter space
$\mathrm {M}_d$
and a critically-marked parameter space
For each degree
![]() $d \geq 2$
, the moduli space
$d \geq 2$
, the moduli space
![]() $\mathrm {M}_d$
is the space of conformal conjugacy classes of maps
$\mathrm {M}_d$
is the space of conformal conjugacy classes of maps
![]() $f: \mathbb {P}^1\to \mathbb {P}^1$
defined over
$f: \mathbb {P}^1\to \mathbb {P}^1$
defined over
![]() $\mathbb {C}$
. It is an affine algebraic variety of dimension
$\mathbb {C}$
. It is an affine algebraic variety of dimension
![]() $2d-2$
. Silverman showed that it exists as a geometric quotient over
$2d-2$
. Silverman showed that it exists as a geometric quotient over
![]() $\operatorname {Spec} \mathbb {Z}$
, and he introduced a projective compactification
$\operatorname {Spec} \mathbb {Z}$
, and he introduced a projective compactification
![]() $\overline {M}_d$
via the tools of Geometric Invariant Theory which can be defined over
$\overline {M}_d$
via the tools of Geometric Invariant Theory which can be defined over
![]() $\mathbb {Q}$
[Reference SilvermanSi1]. We note that
$\mathbb {Q}$
[Reference SilvermanSi1]. We note that
![]() $\mathrm {M}_2 \simeq \mathbb {C}^2$
[Reference MilnorMi1] while
$\mathrm {M}_2 \simeq \mathbb {C}^2$
[Reference MilnorMi1] while
![]() $\mathrm {M}_d$
is singular in all degrees
$\mathrm {M}_d$
is singular in all degrees
![]() $d>2$
[Reference WestWe, Reference Miasnikov, Stout and WilliamsMSW]. Because of the existence of maps with automorphisms, this
$d>2$
[Reference WestWe, Reference Miasnikov, Stout and WilliamsMSW]. Because of the existence of maps with automorphisms, this
![]() $\mathrm {M}_d$
is not a fine moduli space, but we can pass to a finite branched cover
$\mathrm {M}_d$
is not a fine moduli space, but we can pass to a finite branched cover
![]() $\mathcal {M}_d^{cm} \to \mathrm {M}_d$
to build a family
$\mathcal {M}_d^{cm} \to \mathrm {M}_d$
to build a family
of maps, and we may choose
![]() $\mathcal {M}_d^{cm}$
so that we also have functions
$\mathcal {M}_d^{cm}$
so that we also have functions
marking each of the critical points,
![]() $i = 1, \ldots , 2d-2$
.
$i = 1, \ldots , 2d-2$
.
2.2 PCF maps and Thurston rigidity
A map
![]() $f: \mathbb {P}^1 \to \mathbb {P}^1$
is postcritically finite if each of its critical points has a finite forward orbit. An important class of examples of such maps are the Lattès maps, which are quotients of a self-map of a complex torus; the flexible Lattès maps are those that are part of a positive-dimensional family in
$f: \mathbb {P}^1 \to \mathbb {P}^1$
is postcritically finite if each of its critical points has a finite forward orbit. An important class of examples of such maps are the Lattès maps, which are quotients of a self-map of a complex torus; the flexible Lattès maps are those that are part of a positive-dimensional family in
![]() $\mathrm {M}_d$
; see [Reference MilnorMi2] for more information on Lattès maps. We will denote the flexible Lattès locus by
$\mathrm {M}_d$
; see [Reference MilnorMi2] for more information on Lattès maps. We will denote the flexible Lattès locus by
![]() $\mathcal {L}_d$
in
$\mathcal {L}_d$
in
![]() $\mathrm {M}_d$
; it exists only in square degrees. From Thurston’s rigidity theorem [Reference Douady and HubbardDH2], we may deduce that any postcritically finite map which is not flexible Lattès is Möbius-conjugate to a map
$\mathrm {M}_d$
; it exists only in square degrees. From Thurston’s rigidity theorem [Reference Douady and HubbardDH2], we may deduce that any postcritically finite map which is not flexible Lattès is Möbius-conjugate to a map
![]() $f: \mathbb {P}^1\to \mathbb {P}^1$
defined over
$f: \mathbb {P}^1\to \mathbb {P}^1$
defined over
![]() $\overline {\mathbb {Q}}$
.
$\overline {\mathbb {Q}}$
.
2.3 The bifurcation current and its wedge powers
Following [Reference Dujardin and FavreDF], we can define a bifurcation current
![]() $T_i$
on
$T_i$
on
![]() $\mathcal {M}_d^{cm}$
associated to the pair
$\mathcal {M}_d^{cm}$
associated to the pair
![]() $(f,c_i)$
for the map f of (2.1) and each critical point
$(f,c_i)$
for the map f of (2.1) and each critical point
![]() $c_i$
, as follows. We let
$c_i$
, as follows. We let
![]() $\omega $
denote a Fubini-Study form on
$\omega $
denote a Fubini-Study form on
![]() $\mathbb {P}^1$
and let
$\mathbb {P}^1$
and let
![]() $\hat {\omega }$
be its pullback to
$\hat {\omega }$
be its pullback to
![]() $\mathcal {M}_d^{cm} \times \mathbb {P}^1$
by the projection map. Then the sequence of pullbacks
$\mathcal {M}_d^{cm} \times \mathbb {P}^1$
by the projection map. Then the sequence of pullbacks
![]() $\frac {1}{d^n} (f^n)^* \hat \omega $
converge weakly to a current
$\frac {1}{d^n} (f^n)^* \hat \omega $
converge weakly to a current
![]() $\hat {T}_f$
on
$\hat {T}_f$
on
![]() $\mathcal {M}_d^{cm} \times \mathbb {P}^1$
. We let
$\mathcal {M}_d^{cm} \times \mathbb {P}^1$
. We let
where
![]() $\pi : \mathcal {M}_d^{cm} \times \mathbb {P}^1 \to \mathcal {M}_d^{cm}$
is the projection and
$\pi : \mathcal {M}_d^{cm} \times \mathbb {P}^1 \to \mathcal {M}_d^{cm}$
is the projection and
![]() $[\Gamma _{c_i}]$
is the current of integration along the graph of
$[\Gamma _{c_i}]$
is the current of integration along the graph of
![]() $c_i$
. Then
$c_i$
. Then
![]() $T_i$
is a positive (1,1)-current with continuous potentials. The sum
$T_i$
is a positive (1,1)-current with continuous potentials. The sum
 $$ \begin{align} T_{\mathrm{bif}} = \sum_{i = 1}^{2d-2} T_i \end{align} $$
$$ \begin{align} T_{\mathrm{bif}} = \sum_{i = 1}^{2d-2} T_i \end{align} $$
descends to a well-defined positive
![]() $(1,1)$
-current on the moduli space
$(1,1)$
-current on the moduli space
![]() $\mathrm {M}_d$
, and it agrees with the bifurcation current introduced in [Reference DeMarcoDe1]. Because of its continuous potentials, the wedge powers of
$\mathrm {M}_d$
, and it agrees with the bifurcation current introduced in [Reference DeMarcoDe1]. Because of its continuous potentials, the wedge powers of
![]() $T_{\mathrm {bif}}$
are well defined. The bifurcation measure
$T_{\mathrm {bif}}$
are well defined. The bifurcation measure
![]() $T_{\mathrm {bif}}^{\wedge (2d-2)}$
was first introduced in [Reference Bassanelli and BertelootBB] and is non-zero on
$T_{\mathrm {bif}}^{\wedge (2d-2)}$
was first introduced in [Reference Bassanelli and BertelootBB] and is non-zero on
![]() $\mathrm {M}_d$
.
$\mathrm {M}_d$
.
If
![]() $X \subset \mathcal {M}_d^{cm}$
is an irreducible complex algebraic subvariety of dimension
$X \subset \mathcal {M}_d^{cm}$
is an irreducible complex algebraic subvariety of dimension
![]() $r> 0$
whose image in
$r> 0$
whose image in
![]() $\mathrm {M}_d$
is not contained in the flexible Lattès locus
$\mathrm {M}_d$
is not contained in the flexible Lattès locus
![]() $\mathcal {L}_d$
, then
$\mathcal {L}_d$
, then
![]() $T_{\mathrm {bif}} \not =0$
on X, as a consequence of [Reference McMullenMc1, Lemma 2.2] and [Reference DeMarcoDe1, Theorem 1.1]. Moreover,
$T_{\mathrm {bif}} \not =0$
on X, as a consequence of [Reference McMullenMc1, Lemma 2.2] and [Reference DeMarcoDe1, Theorem 1.1]. Moreover,
![]() $T_i = 0$
on X if and only if the critical point
$T_i = 0$
on X if and only if the critical point
![]() $c_i$
is persistently preperiodic along X [Reference Dujardin and FavreDF, Theorem 2.5]. It was proved in [Reference Gauthier, Okuyama and VignyGOV, Lemma 6.8] that we also have
$c_i$
is persistently preperiodic along X [Reference Dujardin and FavreDF, Theorem 2.5]. It was proved in [Reference Gauthier, Okuyama and VignyGOV, Lemma 6.8] that we also have
![]() $T_{\mathrm {bif}}^{\wedge r} \not =0$
on X; in other words, there always exists an r-tuple of critical points
$T_{\mathrm {bif}}^{\wedge r} \not =0$
on X; in other words, there always exists an r-tuple of critical points
![]() $c_{i_1}, \ldots , c_{i_r}$
so that
$c_{i_1}, \ldots , c_{i_r}$
so that
![]() $T_{i_1} \wedge \cdots \wedge T_{i_r} \not =0$
on X.
$T_{i_1} \wedge \cdots \wedge T_{i_r} \not =0$
on X.
2.4 The critical height
For each
![]() $f: \mathbb {P}^1 \to \mathbb {P}^1$
of degree
$f: \mathbb {P}^1 \to \mathbb {P}^1$
of degree
![]() $d>1$
defined over
$d>1$
defined over
![]() $\overline {\mathbb {Q}}$
, recall that the canonical height on
$\overline {\mathbb {Q}}$
, recall that the canonical height on
![]() $\mathbb {P}^1(\overline {\mathbb {Q}})$
is defined by
$\mathbb {P}^1(\overline {\mathbb {Q}})$
is defined by
where h is a Weil height on
![]() $\mathbb {P}^1$
[Reference Call and SilvermanCS]. Counting the critical points with multiplicity, the sum
$\mathbb {P}^1$
[Reference Call and SilvermanCS]. Counting the critical points with multiplicity, the sum
 $$ \begin{align*}\hat{h}_{\mathrm{crit}}(f) := \sum_{\{c~: ~f'(c)=0\}} \hat{h}_f(c)\end{align*} $$
$$ \begin{align*}\hat{h}_{\mathrm{crit}}(f) := \sum_{\{c~: ~f'(c)=0\}} \hat{h}_f(c)\end{align*} $$
defines a function on
![]() $\mathcal {M}_d^{cm}$
, which Silverman called the critical height and conjectured that it is comparable with a Weil height on
$\mathcal {M}_d^{cm}$
, which Silverman called the critical height and conjectured that it is comparable with a Weil height on
![]() $\mathrm {M}_d \setminus \mathcal {L}_d$
; see, for example, [Reference SilvermanSi2]. This comparability was proved by Ingram in [Reference IngramIn].
$\mathrm {M}_d \setminus \mathcal {L}_d$
; see, for example, [Reference SilvermanSi2]. This comparability was proved by Ingram in [Reference IngramIn].
The construction of the critical height was revisited by Yuan and Zhang in [Reference Yuan and ZhangYZ, §6.3], where they show that
![]() $\hat {h}_{\mathrm {crit}}$
is the height associated to a non-degenerate adelically metrized line bundle on
$\hat {h}_{\mathrm {crit}}$
is the height associated to a non-degenerate adelically metrized line bundle on
![]() $\mathcal {M}^{cm}_d$
over
$\mathcal {M}^{cm}_d$
over
![]() $\mathbb {Q}$
. Indeed, they construct an f-invariant adelic line bundle
$\mathbb {Q}$
. Indeed, they construct an f-invariant adelic line bundle
![]() $\overline {L}_f$
on
$\overline {L}_f$
on
![]() $\mathcal {M}_d^{cm} \times \mathbb {P}^1$
for the f of (2.1). The critical height is then the height function associated to the “restriction” of
$\mathcal {M}_d^{cm} \times \mathbb {P}^1$
for the f of (2.1). The critical height is then the height function associated to the “restriction” of
![]() $\overline {L}_f$
to the ramification divisor of f; see [Reference Yuan and ZhangYZ, §6.3]. Important for us is that the curvature distribution at the archimedean place is equal to the bifurcation current
$\overline {L}_f$
to the ramification divisor of f; see [Reference Yuan and ZhangYZ, §6.3]. Important for us is that the curvature distribution at the archimedean place is equal to the bifurcation current
![]() $T_{\mathrm {bif}}$
defined in §2.3. The non-degeneracy of this metrized line bundle follows because the bifurcation measure is non-trivial, as was proved in [Reference Bassanelli and BertelootBB].
$T_{\mathrm {bif}}$
defined in §2.3. The non-degeneracy of this metrized line bundle follows because the bifurcation measure is non-trivial, as was proved in [Reference Bassanelli and BertelootBB].
Yuan and Zhang use their general equidistribution theorem [Reference Yuan and ZhangYZ, Theorem 5.4.3] to give an alternative proof of the arithmetic equidistribution of the points in
![]() $\mathrm {PCF}_d$
to the bifurcation measure
$\mathrm {PCF}_d$
to the bifurcation measure
![]() $T_{\mathrm {bif}}^{\wedge 2d-2}$
in [Reference Yuan and ZhangYZ, §6.3], a result which was first obtained by Gauthier in [Reference GauthierGa3] (and was proved for the polynomial moduli spaces in [Reference Favre and GauthierFG1]).
$T_{\mathrm {bif}}^{\wedge 2d-2}$
in [Reference Yuan and ZhangYZ, §6.3], a result which was first obtained by Gauthier in [Reference GauthierGa3] (and was proved for the polynomial moduli spaces in [Reference Favre and GauthierFG1]).
2.5 The Chow variety and maximal variation
For general information about Chow varieties, we refer the reader to [Reference Gelfand, Kapranov and ZelevinskyGKZ] [Reference KollárKo]. Here we fix notation and state some basic properties that we need. We will apply the following discussion to
![]() $Y = \mathrm {M}_d$
or
$Y = \mathrm {M}_d$
or
![]() $Y = \mathcal {M}_d^{cm}$
.
$Y = \mathcal {M}_d^{cm}$
.
Suppose that Y is an irreducible quasiprojective algebraic variety, equipped with a projective embedding of
![]() $Y \hookrightarrow \mathbb {P}^N$
defined over
$Y \hookrightarrow \mathbb {P}^N$
defined over
![]() $\mathbb {Q}$
. We let
$\mathbb {Q}$
. We let
![]() $\overline {Y}$
denote the closure of Y in
$\overline {Y}$
denote the closure of Y in
![]() $\mathbb {P}^N$
. For each integer
$\mathbb {P}^N$
. For each integer
![]() $0 \leq r < \dim Y$
, and with respect to this embedding, we first consider the Chow variety
$0 \leq r < \dim Y$
, and with respect to this embedding, we first consider the Chow variety
![]() $\mathrm {Ch}(\overline {Y}, r, D)$
of algebraic cycles
$\mathrm {Ch}(\overline {Y}, r, D)$
of algebraic cycles
![]() $X \subset \overline {Y}$
in dimension r with degree
$X \subset \overline {Y}$
in dimension r with degree
![]() $\leq D$
. It is an algebraic subvariety, possibly reducible, of the Chow variety
$\leq D$
. It is an algebraic subvariety, possibly reducible, of the Chow variety
![]() $\mathrm {Ch}(\mathbb {P}^N, r, D)$
, consisting of the cycles with dimension r and degree
$\mathrm {Ch}(\mathbb {P}^N, r, D)$
, consisting of the cycles with dimension r and degree
![]() $\leq D$
supported in
$\leq D$
supported in
![]() $\overline {Y}$
. As
$\overline {Y}$
. As
![]() $\overline {Y}$
is defined over
$\overline {Y}$
is defined over
![]() $\mathbb {Q}$
, the Chow variety
$\mathbb {Q}$
, the Chow variety
![]() $\mathrm {Ch}(\overline {Y}, r, D)$
is also defined over
$\mathrm {Ch}(\overline {Y}, r, D)$
is also defined over
![]() $\mathbb {Q}$
. We let
$\mathbb {Q}$
. We let
![]() $\mathrm {Ch}(Y, r, D)$
denote the Zariski-open subset consisting of cycles with support intersecting Y.
$\mathrm {Ch}(Y, r, D)$
denote the Zariski-open subset consisting of cycles with support intersecting Y.
We will say that an irreducible subvariety
![]() $X \subset Y$
of dimension r has degree
$X \subset Y$
of dimension r has degree
![]() $\boldsymbol {\leq D}$
if its Zariski closure in
$\boldsymbol {\leq D}$
if its Zariski closure in
![]() $\overline {Y}$
is the support of a cycle represented by a point in
$\overline {Y}$
is the support of a cycle represented by a point in
![]() $\mathrm {Ch}(Y, r, D)$
. Note that the degree depends on the choice of the embedding of Y into
$\mathrm {Ch}(Y, r, D)$
. Note that the degree depends on the choice of the embedding of Y into
![]() $\mathbb {P}^N$
, but the concept of bounded degree does not.
$\mathbb {P}^N$
, but the concept of bounded degree does not.
Suppose that
![]() $\pi : \mathcal {X}\to V$
is a family of r-dimensional varieties in Y, parametrized by
$\pi : \mathcal {X}\to V$
is a family of r-dimensional varieties in Y, parametrized by
![]() $\lambda $
in an irreducible quasi-projective variety V of dimension
$\lambda $
in an irreducible quasi-projective variety V of dimension
![]() $\ell \ge 1$
. Assume that the generic fiber of
$\ell \ge 1$
. Assume that the generic fiber of
![]() $\mathcal {X} \to V$
is geometrically irreducible. We say that
$\mathcal {X} \to V$
is geometrically irreducible. We say that
![]() $\mathcal {X}\to V$
is maximally varying if the natural map from V to the Chow variety
$\mathcal {X}\to V$
is maximally varying if the natural map from V to the Chow variety
![]() $\mathrm {Ch}(Y, r, D)$
has finite fibers, where we send each irreducible fiber
$\mathrm {Ch}(Y, r, D)$
has finite fibers, where we send each irreducible fiber
![]() $X_\lambda := \pi ^{-1}(\lambda )$
to the point of
$X_\lambda := \pi ^{-1}(\lambda )$
to the point of
![]() $\mathrm {Ch}(Y, r, D)$
representing the cycle
$\mathrm {Ch}(Y, r, D)$
representing the cycle
![]() $[\overline {X}_\lambda ]$
on
$[\overline {X}_\lambda ]$
on
![]() $\overline {Y}$
.
$\overline {Y}$
.
For any positive integer m, recall that
![]() $\mathcal {X}_V^m$
denotes the m-th fiber power of
$\mathcal {X}_V^m$
denotes the m-th fiber power of
![]() $\mathcal {X}$
over V. There is a natural map
$\mathcal {X}$
over V. There is a natural map
defined by
![]() $\rho _m(\lambda ,f_1,\ldots ,f_{m})=(f_1,\ldots ,f_{m})$
.
$\rho _m(\lambda ,f_1,\ldots ,f_{m})=(f_1,\ldots ,f_{m})$
.
Proposition 2.1. Suppose that Y is an irreducible quasiprojective complex algebraic variety. Suppose that
![]() $\mathcal {X}\to V$
is a family of r-dimensional varieties
$\mathcal {X}\to V$
is a family of r-dimensional varieties
![]() $X_{\lambda }\subset Y$
, parametrized by
$X_{\lambda }\subset Y$
, parametrized by
![]() $\lambda $
in a quasi-projective variety V of dimension
$\lambda $
in a quasi-projective variety V of dimension
![]() $\ell \ge 1$
. Assume that V and the generic fiber of
$\ell \ge 1$
. Assume that V and the generic fiber of
![]() $\mathcal {X} \to V$
are irreducible. If
$\mathcal {X} \to V$
are irreducible. If
![]() $\mathcal {X} \to V$
is maximally varying, then the map
$\mathcal {X} \to V$
is maximally varying, then the map
is generically finite. In particular
![]() $\dim \rho _\ell (\mathcal {X}^{\ell }_V) = \dim \mathcal {X}_V^{\ell }$
.
$\dim \rho _\ell (\mathcal {X}^{\ell }_V) = \dim \mathcal {X}_V^{\ell }$
.
Proof. We prove the result by induction on
![]() $\ell $
. For
$\ell $
. For
![]() $\ell = 1$
, the result is clear, as
$\ell = 1$
, the result is clear, as
![]() $\dim \mathcal {X} = r+1$
and maximal variation implies that the image of
$\dim \mathcal {X} = r+1$
and maximal variation implies that the image of
![]() $\mathcal {X}$
in Y is not contained in an r-dimensional subvariety, so
$\mathcal {X}$
in Y is not contained in an r-dimensional subvariety, so
![]() $\dim \rho _1(\mathcal {X}) = \dim \mathcal {X} = r+1$
.
$\dim \rho _1(\mathcal {X}) = \dim \mathcal {X} = r+1$
.
Now suppose
![]() $\ell> 1$
and that we know the result for maximally varying families with base dimension
$\ell> 1$
and that we know the result for maximally varying families with base dimension
![]() $< \ell $
. Note that
$< \ell $
. Note that
![]() $\dim \mathcal {X} = \ell + r$
and
$\dim \mathcal {X} = \ell + r$
and
![]() $\dim \mathcal {X}_V^\ell = \ell (r+1)$
. Choose any smooth point
$\dim \mathcal {X}_V^\ell = \ell (r+1)$
. Choose any smooth point
![]() $x_0$
of
$x_0$
of
![]() $\rho _1(\mathcal {X})$
which is also smooth for a subvariety
$\rho _1(\mathcal {X})$
which is also smooth for a subvariety
![]() $X_{\lambda _0}$
it lies in, and which is regular for the maps
$X_{\lambda _0}$
it lies in, and which is regular for the maps
![]() $\rho _1: \mathcal {X} \to \rho _1(\mathcal {X})$
and
$\rho _1: \mathcal {X} \to \rho _1(\mathcal {X})$
and
![]() $\pi _1: \rho _\ell (\mathcal {X}_V^\ell ) \to \rho _1(\mathcal {X})$
where the latter is the restriction of the projection
$\pi _1: \rho _\ell (\mathcal {X}_V^\ell ) \to \rho _1(\mathcal {X})$
where the latter is the restriction of the projection
![]() $Y^\ell \to Y$
to the first coordinate. Here, “regular for the maps” means that the fiber over
$Y^\ell \to Y$
to the first coordinate. Here, “regular for the maps” means that the fiber over
![]() $x_0$
has the expected dimension and there is a point in the fiber over
$x_0$
has the expected dimension and there is a point in the fiber over
![]() $x_0$
mapping surjectively on tangent spaces to that of
$x_0$
mapping surjectively on tangent spaces to that of
![]() $x_0$
.
$x_0$
.
Let
![]() $Y_1 \subset \rho _1(\mathcal {X}) \subset Y$
be a subvariety of codimension r in
$Y_1 \subset \rho _1(\mathcal {X}) \subset Y$
be a subvariety of codimension r in
![]() $\rho _1(\mathcal {X})$
containing
$\rho _1(\mathcal {X})$
containing
![]() $x_0$
, intersecting
$x_0$
, intersecting
![]() $X_{\lambda _0}$
(and therefore a general
$X_{\lambda _0}$
(and therefore a general
![]() $X_\lambda $
) in a finite set. Consider the projection
$X_\lambda $
) in a finite set. Consider the projection
![]() $p_1: \mathcal {X}_V^{\ell } \to \mathcal {X}$
to the first factor and the projection
$p_1: \mathcal {X}_V^{\ell } \to \mathcal {X}$
to the first factor and the projection
![]() $p_2: \mathcal {X}_V^{\ell } \to \mathcal {X}_V^{\ell -1}$
to the remaining
$p_2: \mathcal {X}_V^{\ell } \to \mathcal {X}_V^{\ell -1}$
to the remaining
![]() $\ell -1$
factors. Note that
$\ell -1$
factors. Note that
![]() $\rho _1^{-1}(Y_1) \subset \mathcal {X}$
projects dominantly to the base V, and
$\rho _1^{-1}(Y_1) \subset \mathcal {X}$
projects dominantly to the base V, and
![]() $p_1^{-1}(\rho _1^{-1}(Y_1))$
projects dominantly and generically finitely by
$p_1^{-1}(\rho _1^{-1}(Y_1))$
projects dominantly and generically finitely by
![]() $p_2$
to
$p_2$
to
![]() $\mathcal {X}_V^{\ell -1}$
.
$\mathcal {X}_V^{\ell -1}$
.
Now choose any
![]() $Y_1' \subset Y_1$
of codimension 1 containing
$Y_1' \subset Y_1$
of codimension 1 containing
![]() $x_0$
, so of codimension
$x_0$
, so of codimension
![]() $r+1$
in
$r+1$
in
![]() $\rho _1(\mathcal {X})$
. Then
$\rho _1(\mathcal {X})$
. Then
![]() $\rho _1^{-1}(Y_1')$
has codimension
$\rho _1^{-1}(Y_1')$
has codimension
![]() $r+1$
in
$r+1$
in
![]() $\mathcal {X}$
, and its projection to the base V will be a subvariety
$\mathcal {X}$
, and its projection to the base V will be a subvariety
![]() $V_1$
of codimension 1. Let
$V_1$
of codimension 1. Let
![]() $\mathcal {X}|_{V_1} \to V_1$
denote the restricted family over the
$\mathcal {X}|_{V_1} \to V_1$
denote the restricted family over the
![]() $(\ell -1)$
-dimensional base. Note that
$(\ell -1)$
-dimensional base. Note that
![]() $p_1^{-1}(\rho _1^{-1}(Y_1'))$
is contained in
$p_1^{-1}(\rho _1^{-1}(Y_1'))$
is contained in
![]() $\mathcal {X}_{V_1}^\ell $
and projects dominantly and generically finitely by
$\mathcal {X}_{V_1}^\ell $
and projects dominantly and generically finitely by
![]() $p_2$
to
$p_2$
to
![]() $\mathcal {X}_{V_1}^{\ell -1}$
.
$\mathcal {X}_{V_1}^{\ell -1}$
.
By induction we know that
![]() $\dim \rho _{\ell -1}(\mathcal {X}_{V_1}^{\ell -1}) = \dim \mathcal {X}_{V_1}^{\ell -1} = (\ell - 1)(r+1) = \ell (r+1) - (r+1)$
. Therefore
$\dim \rho _{\ell -1}(\mathcal {X}_{V_1}^{\ell -1}) = \dim \mathcal {X}_{V_1}^{\ell -1} = (\ell - 1)(r+1) = \ell (r+1) - (r+1)$
. Therefore
Now consider
![]() $\pi _1^{-1}(Y_1')$
in
$\pi _1^{-1}(Y_1')$
in
![]() $\rho _\ell (\mathcal {X}_V^\ell )$
, which also has codimension
$\rho _\ell (\mathcal {X}_V^\ell )$
, which also has codimension
![]() $r+1$
by the choice of
$r+1$
by the choice of
![]() $x_0$
. But
$x_0$
. But
![]() $\pi _1 \circ \rho _\ell = \rho _1\circ p_1$
, so that
$\pi _1 \circ \rho _\ell = \rho _1\circ p_1$
, so that
implying that
and the proof is complete.
3 Bifurcation measures on
 $\mathcal {X}_V^{\hspace{1pt}\ell} $
and
$\mathcal {X}_V^{\hspace{1pt}\ell} $
and
 $\mathcal {X}_V^{\hspace{1pt}\ell +1}$
$\mathcal {X}_V^{\hspace{1pt}\ell +1}$
Recall the definition of
![]() $\mathcal {M}_d^{cm}$
from §2.1. Throughout this section, we assume that
$\mathcal {M}_d^{cm}$
from §2.1. Throughout this section, we assume that
![]() $\mathcal {X}\to V$
is a maximally varying family of r-dimensional varieties
$\mathcal {X}\to V$
is a maximally varying family of r-dimensional varieties
![]() $X_{\lambda }\subset \mathcal {M}_d^{cm}$
, parametrized by
$X_{\lambda }\subset \mathcal {M}_d^{cm}$
, parametrized by
![]() $\lambda $
in a quasi-projective variety V of dimension
$\lambda $
in a quasi-projective variety V of dimension
![]() $\ell \ge 1$
. Assume that V and the generic fiber of
$\ell \ge 1$
. Assume that V and the generic fiber of
![]() $\mathcal {X} \to V$
are irreducible. For any positive integer m, recall from §1.2 that
$\mathcal {X} \to V$
are irreducible. For any positive integer m, recall from §1.2 that
![]() $\mathcal {X}_V^m$
denotes the m-th fiber power of
$\mathcal {X}_V^m$
denotes the m-th fiber power of
![]() $\mathcal {X}$
over V, and we denote elements of
$\mathcal {X}$
over V, and we denote elements of
![]() $\mathcal {X}_V^{m}$
by
$\mathcal {X}_V^{m}$
by
![]() $(\lambda , f_1, \ldots , f_m)$
, with
$(\lambda , f_1, \ldots , f_m)$
, with
![]() $f_i \in X_\lambda $
for each i. There is a natural map
$f_i \in X_\lambda $
for each i. There is a natural map
defined by
![]() $\rho _m(\lambda ,f_1,\ldots ,f_{m})=(f_1,\ldots ,f_{m})$
. From Proposition 2.1, we know that
$\rho _m(\lambda ,f_1,\ldots ,f_{m})=(f_1,\ldots ,f_{m})$
. From Proposition 2.1, we know that
![]() $\rho _m$
is generically finite for all
$\rho _m$
is generically finite for all
![]() $m \geq \ell $
.
$m \geq \ell $
.
In this section we construct nontrivial measures on
![]() $\mathcal {X}_V^{\ell }$
and
$\mathcal {X}_V^{\ell }$
and
![]() $\mathcal {X}_V^{\ell +1}$
that are pullbacks of powers of the bifurcation currents in
$\mathcal {X}_V^{\ell +1}$
that are pullbacks of powers of the bifurcation currents in
![]() $\mathcal {M}_d^{cm}$
, defined in §2.3. The measure on
$\mathcal {M}_d^{cm}$
, defined in §2.3. The measure on
![]() $\mathcal {X}_V^{\ell }$
will be defined in terms of
$\mathcal {X}_V^{\ell }$
will be defined in terms of
![]() $T_{\mathrm {bif}}$
of (2.3), while two measures on
$T_{\mathrm {bif}}$
of (2.3), while two measures on
![]() $\mathcal {X}_V^{\ell +1}$
will additionally involve choices of r-tuples of marked critical points. The proofs build on the strong rigidity result that the power
$\mathcal {X}_V^{\ell +1}$
will additionally involve choices of r-tuples of marked critical points. The proofs build on the strong rigidity result that the power
![]() $T_{\mathrm {bif}}^{\wedge r}$
of the bifurcation current is nonzero on every r-dimensional subvariety of
$T_{\mathrm {bif}}^{\wedge r}$
of the bifurcation current is nonzero on every r-dimensional subvariety of
![]() $\mathrm {M}_d\setminus \mathcal {L}_d$
, where
$\mathrm {M}_d\setminus \mathcal {L}_d$
, where
![]() $\mathcal {L}_d$
is the flexible Lattès locus; this is proved in [Reference Gauthier, Okuyama and VignyGOV, Lemma 6.8] for all r. (See the discussion in §2.3.)
$\mathcal {L}_d$
is the flexible Lattès locus; this is proved in [Reference Gauthier, Okuyama and VignyGOV, Lemma 6.8] for all r. (See the discussion in §2.3.)
We also appeal to descriptions of the support of powers of
![]() $T_{\mathrm {bif}}$
in
$T_{\mathrm {bif}}$
in
![]() $\mathrm {M}_d$
in terms of critical orbit behavior obtained by Buff-Epstein in [Reference Buff and EpsteinBE] and Dujardin in [Reference DujardinDu]. Precisely, suppose that
$\mathrm {M}_d$
in terms of critical orbit behavior obtained by Buff-Epstein in [Reference Buff and EpsteinBE] and Dujardin in [Reference DujardinDu]. Precisely, suppose that
![]() $f_1, \ldots , f_m$
is a collection of holomorphic families of maps on
$f_1, \ldots , f_m$
is a collection of holomorphic families of maps on
![]() $\mathbb {P}^1$
parameterized by
$\mathbb {P}^1$
parameterized by
![]() $\lambda $
in a complex manifold
$\lambda $
in a complex manifold
![]() $\Lambda $
, and let
$\Lambda $
, and let
![]() $\Phi := (f_1, \ldots , f_m): \Lambda \times (\mathbb {P}^1)^m \to \Lambda \times (\mathbb {P}^1)^m$
be the induced holomorphic map. We say that an m-tuple of marked points
$\Phi := (f_1, \ldots , f_m): \Lambda \times (\mathbb {P}^1)^m \to \Lambda \times (\mathbb {P}^1)^m$
be the induced holomorphic map. We say that an m-tuple of marked points
![]() $\mathbf {a} = (a_1, \ldots , a_m): \Lambda \to (\mathbb {P}^1)^m$
is transversely (respectively, properly) prerepelling for
$\mathbf {a} = (a_1, \ldots , a_m): \Lambda \to (\mathbb {P}^1)^m$
is transversely (respectively, properly) prerepelling for
![]() $\boldsymbol {\Phi }$
at
$\boldsymbol {\Phi }$
at
![]() $\boldsymbol {\lambda _0}$
over
$\boldsymbol {\lambda _0}$
over
![]() $\boldsymbol {\Lambda }$
if there exist repelling periodic points
$\boldsymbol {\Lambda }$
if there exist repelling periodic points
![]() $p_i$
of
$p_i$
of
![]() $f_{\lambda _0}$
and integers
$f_{\lambda _0}$
and integers
![]() $n_i \ge 1$
such that
$n_i \ge 1$
such that
![]() $f_{\lambda _0}^{n_i}(a_i(\lambda _0)) = p_i$
for each
$f_{\lambda _0}^{n_i}(a_i(\lambda _0)) = p_i$
for each
![]() $i = 1, \ldots , m$
, and the following holds: if
$i = 1, \ldots , m$
, and the following holds: if
![]() $p_i: U \to \mathbb {P}^1$
denotes the holomorphic continuation of the repelling periodic point
$p_i: U \to \mathbb {P}^1$
denotes the holomorphic continuation of the repelling periodic point
![]() $p_i=p_i(\lambda _0)$
over some neighborhood
$p_i=p_i(\lambda _0)$
over some neighborhood
![]() $U \subset \Lambda $
of
$U \subset \Lambda $
of
![]() $\lambda _0$
where it remains repelling, then the graphs of the maps
$\lambda _0$
where it remains repelling, then the graphs of the maps
intersect transversely (respectively, properly) in
![]() $U \times (\mathbb {P}^1)^m$
at
$U \times (\mathbb {P}^1)^m$
at
![]() $\lambda _0$
.
$\lambda _0$
.
For positive integers
![]() $m \leq 2d-2$
, marked critical points
$m \leq 2d-2$
, marked critical points
![]() $\mathbf {c} = (c_1, \ldots , c_m)$
, and
$\mathbf {c} = (c_1, \ldots , c_m)$
, and
![]() $f_1 = \cdots = f_m := f$
, Dujardin proved that there is a dense set of parameters in
$f_1 = \cdots = f_m := f$
, Dujardin proved that there is a dense set of parameters in
![]() $\operatorname {supp} T_1 \wedge \cdots \wedge T_m$
in
$\operatorname {supp} T_1 \wedge \cdots \wedge T_m$
in
![]() $\mathcal {M}_d^{cm}$
at which
$\mathcal {M}_d^{cm}$
at which
![]() $\mathbf {c}$
is transversely prerepelling over
$\mathbf {c}$
is transversely prerepelling over
![]() $\mathcal {M}_d^{cm}$
[Reference DujardinDu, Theorem 1.1]; recall that
$\mathcal {M}_d^{cm}$
[Reference DujardinDu, Theorem 1.1]; recall that
![]() $T_i$
was defined in (2.2). And conversely, if the m-tuple of critical points is properly prerepelling for
$T_i$
was defined in (2.2). And conversely, if the m-tuple of critical points is properly prerepelling for
![]() $(f,\ldots , f)$
at some parameter
$(f,\ldots , f)$
at some parameter
![]() $\lambda _0$
over a parameter space of dimension
$\lambda _0$
over a parameter space of dimension
![]() $\geq m$
, then
$\geq m$
, then
![]() $T_1 \wedge \cdots \wedge T_m$
must be nonzero in that parameter space with
$T_1 \wedge \cdots \wedge T_m$
must be nonzero in that parameter space with
![]() $\lambda _0$
in its support, as first observed in [Reference Buff and EpsteinBE] (where it was proved in the case
$\lambda _0$
in its support, as first observed in [Reference Buff and EpsteinBE] (where it was proved in the case
![]() $m=2d-2$
and assuming transversely prerepelling) and revisited in [Reference GauthierGa1, Theorem 6.2], [Reference GauthierGa2, Theorem 2.3], and [Reference Berteloot, Bianchi and DupontBBD, Proposition 3.7] in more general contexts and without assuming transversality. See [Reference DeMarco and MavrakiDM1, Proposition 4.8] for the version we use, which implies that the latter converse result remains true with any m-tuple of maps
$m=2d-2$
and assuming transversely prerepelling) and revisited in [Reference GauthierGa1, Theorem 6.2], [Reference GauthierGa2, Theorem 2.3], and [Reference Berteloot, Bianchi and DupontBBD, Proposition 3.7] in more general contexts and without assuming transversality. See [Reference DeMarco and MavrakiDM1, Proposition 4.8] for the version we use, which implies that the latter converse result remains true with any m-tuple of maps
![]() $(f_1,\ldots , f_m)$
of degree d in place of
$(f_1,\ldots , f_m)$
of degree d in place of
![]() $(f,\ldots ,f)$
.
$(f,\ldots ,f)$
.
3.1 Measure on
 $\mathcal {X}_V^{\hspace{1pt}\ell} $
$\mathcal {X}_V^{\hspace{1pt}\ell} $
Proposition 3.1. Let
![]() $\mathcal {X}\to V$
be a maximally varying family of dimension
$\mathcal {X}\to V$
be a maximally varying family of dimension
![]() $r\ge 1$
varieties in
$r\ge 1$
varieties in
![]() $\mathcal {M}_d^{cm}$
with
$\mathcal {M}_d^{cm}$
with
![]() $\dim V = \ell \geq 1$
, and let
$\dim V = \ell \geq 1$
, and let
![]() $\rho _{\ell }$
be the map of (3.1) for
$\rho _{\ell }$
be the map of (3.1) for
![]() $m = \ell $
. Set
$m = \ell $
. Set
![]() $\mathcal {Y}_\ell = \rho _\ell (\mathcal {X}_V^\ell )$
. Let
$\mathcal {Y}_\ell = \rho _\ell (\mathcal {X}_V^\ell )$
. Let
![]() $T_{\mathrm {bif}}$
denote the bifurcation current in
$T_{\mathrm {bif}}$
denote the bifurcation current in
![]() $\mathcal {M}_d^{cm}$
and let
$\mathcal {M}_d^{cm}$
and let
![]() $\pi _i: (\mathcal {M}_d^{cm})^{\ell }\to \mathcal {M}_d^{cm}$
be the projection to the i-th factor for
$\pi _i: (\mathcal {M}_d^{cm})^{\ell }\to \mathcal {M}_d^{cm}$
be the projection to the i-th factor for
![]() $i=1,\ldots ,\ell $
. Then
$i=1,\ldots ,\ell $
. Then
in
![]() $(\mathcal {M}_d^{cm})^\ell $
, so that
$(\mathcal {M}_d^{cm})^\ell $
, so that
defines a positive measure on
![]() $\mathcal {X}_V^\ell $
. Moreover, there is a collection of marked critical points
$\mathcal {X}_V^\ell $
. Moreover, there is a collection of marked critical points
defined on
![]() $\mathcal {X}_V^\ell $
which is transversely prerepelling for the family of product maps
$\mathcal {X}_V^\ell $
which is transversely prerepelling for the family of product maps
at a parameter
![]() $x_0$
over
$x_0$
over
![]() $\mathcal {X}_V^\ell $
, where each
$\mathcal {X}_V^\ell $
, where each
![]() $f_i$
is repeated
$f_i$
is repeated
![]() $r+1$
times.
$r+1$
times.
If
![]() $\mathbf {c}$
satisfies the conclusion of Proposition 3.1 for
$\mathbf {c}$
satisfies the conclusion of Proposition 3.1 for
![]() $\Phi $
, we say that it witnesses the nonvanishing of
$\Phi $
, we say that it witnesses the nonvanishing of
![]() $\mu _\ell $
.
$\mu _\ell $
.
Proof. Let
![]() $\mathcal {Y} \subset \mathcal {M}_d^{cm}$
be the image of
$\mathcal {Y} \subset \mathcal {M}_d^{cm}$
be the image of
![]() $\rho _1$
, and let k be the dimension of
$\rho _1$
, and let k be the dimension of
![]() $\mathcal {Y}$
, so that
$\mathcal {Y}$
, so that
Since the projection
![]() $\mathcal {M}_d^{cm} \to \mathrm {M}_d$
has finite fibers, we know from [Reference Gauthier, Okuyama and VignyGOV, Lemma 6.8] that
$\mathcal {M}_d^{cm} \to \mathrm {M}_d$
has finite fibers, we know from [Reference Gauthier, Okuyama and VignyGOV, Lemma 6.8] that
![]() $T_{\mathrm {bif}}^{\wedge k} \not =0$
on
$T_{\mathrm {bif}}^{\wedge k} \not =0$
on
![]() $\mathcal {Y}$
.
$\mathcal {Y}$
.
If
![]() $\ell =1$
, then we are done, since
$\ell =1$
, then we are done, since
![]() $k = r+1$
and
$k = r+1$
and
![]() $T_{\mathrm {bif}}^{\wedge (r+1)} \wedge [\mathcal {Y}]$
in
$T_{\mathrm {bif}}^{\wedge (r+1)} \wedge [\mathcal {Y}]$
in
![]() $\mathcal {M}_d^{cm}$
.
$\mathcal {M}_d^{cm}$
.
Assume
![]() $\ell> 1$
. Let
$\ell> 1$
. Let
denote the family of product maps on
![]() $(\mathbb {P}^1)^{\ell (r+1)}$
parameterized by
$(\mathbb {P}^1)^{\ell (r+1)}$
parameterized by
![]() $\mathcal {Y}_\ell \subset (\mathcal {M}_d^{cm})^\ell $
, where each coordinate
$\mathcal {Y}_\ell \subset (\mathcal {M}_d^{cm})^\ell $
, where each coordinate
![]() $f_i$
is repeated
$f_i$
is repeated
![]() $r+1$
times.
$r+1$
times.
Let
![]() $U\subset \mathcal {Y}$
be a Zariski-open set so that the fibers of the two maps
$U\subset \mathcal {Y}$
be a Zariski-open set so that the fibers of the two maps
![]() $\rho _1: \mathcal {X} \to \mathcal {Y}$
and
$\rho _1: \mathcal {X} \to \mathcal {Y}$
and
![]() $\pi _1: \mathcal {Y}_\ell \to \mathcal {Y}$
to the first factor of
$\pi _1: \mathcal {Y}_\ell \to \mathcal {Y}$
to the first factor of
![]() $(\mathcal {M}_d^{cm})^\ell $
have the expected dimension over U, namely
$(\mathcal {M}_d^{cm})^\ell $
have the expected dimension over U, namely
![]() $r+\ell -k$
for fibers of
$r+\ell -k$
for fibers of
![]() $\rho _1$
and
$\rho _1$
and
![]() $\ell + r\ell - k$
for
$\ell + r\ell - k$
for
![]() $\pi _1$
, and the maps are surjective on tangent spaces at some point of each fiber over elements of U. Note that, by the symmetry of
$\pi _1$
, and the maps are surjective on tangent spaces at some point of each fiber over elements of U. Note that, by the symmetry of
![]() $\mathcal {Y}_\ell $
, the fibers will have the same properties for projections
$\mathcal {Y}_\ell $
, the fibers will have the same properties for projections
![]() $\pi _i$
for each i. From [Reference DujardinDu, Theorem 1.1], there exists a k-tuple of critical points
$\pi _i$
for each i. From [Reference DujardinDu, Theorem 1.1], there exists a k-tuple of critical points
![]() $\{c_1, \ldots , c_k\}$
and a parameter
$\{c_1, \ldots , c_k\}$
and a parameter
![]() $y_0 \in U$
in the support of
$y_0 \in U$
in the support of
![]() $T_{\mathrm {bif}}^{\wedge k}$
at which these critical points are transversely prerepelling for the family of maps
$T_{\mathrm {bif}}^{\wedge k}$
at which these critical points are transversely prerepelling for the family of maps
![]() $f_1$
parameterized by U. We may assume that
$f_1$
parameterized by U. We may assume that
![]() $y_0$
is a smooth point of
$y_0$
is a smooth point of
![]() $\mathcal {Y}$
and of the subvariety
$\mathcal {Y}$
and of the subvariety
![]() $X_{\lambda _0}$
for a smooth parameter
$X_{\lambda _0}$
for a smooth parameter
![]() $\lambda _0 \in V$
.
$\lambda _0 \in V$
.
Now choose a collection of
![]() $r+1$
critical points
$r+1$
critical points
![]() $c_{1,1}, \ldots , c_{1,r+1} \in \{c_1, \ldots , c_k\}$
so that
$c_{1,1}, \ldots , c_{1,r+1} \in \{c_1, \ldots , c_k\}$
so that
![]() $(c_{1,1}, \ldots , c_{1,r})$
is transversely prerepelling at
$(c_{1,1}, \ldots , c_{1,r})$
is transversely prerepelling at
![]() $y_0$
over
$y_0$
over
![]() $X_{\lambda _0}$
and the full
$X_{\lambda _0}$
and the full
![]() $(r+1)$
-tuple is transversely prerepelling at
$(r+1)$
-tuple is transversely prerepelling at
![]() $y_0$
over U. Let
$y_0$
over U. Let
![]() $Z_1 \subset U$
be an irreducible component of the codimension-
$Z_1 \subset U$
be an irreducible component of the codimension-
![]() $(r+1)$
subvariety containing
$(r+1)$
subvariety containing
![]() $y_0$
where these critical points are persistently preperiodic. Note that
$y_0$
where these critical points are persistently preperiodic. Note that
![]() $y_0$
is an isolated point of the intersection of
$y_0$
is an isolated point of the intersection of
![]() $Z_1$
with
$Z_1$
with
![]() $X_{\lambda _0}$
. Moreover, we know that
$X_{\lambda _0}$
. Moreover, we know that
![]() $\pi _1^{-1}(Z_1)$
has codimension
$\pi _1^{-1}(Z_1)$
has codimension
![]() $r+1$
in
$r+1$
in
![]() $\mathcal {Y}_\ell $
.
$\mathcal {Y}_\ell $
.
Note that the preimage
![]() $\rho _\ell ^{-1}(\pi _1^{-1}(Z_1))$
in
$\rho _\ell ^{-1}(\pi _1^{-1}(Z_1))$
in
![]() $\mathcal {X}_V^{\ell }$
projects to a subvariety
$\mathcal {X}_V^{\ell }$
projects to a subvariety
![]() $V_1$
of codimension 1 in the base V. In fact it maps with finite fibers to the
$V_1$
of codimension 1 in the base V. In fact it maps with finite fibers to the
![]() $(\ell -1)$
-th fiber power of a subfamily
$(\ell -1)$
-th fiber power of a subfamily
where
![]() $\dim V_1 = \ell -1$
. Now let
$\dim V_1 = \ell -1$
. Now let
![]() $\mathcal {Y}_1$
be the image of this subfamily
$\mathcal {Y}_1$
be the image of this subfamily
![]() $\mathcal {X}|_{V_1}$
in
$\mathcal {X}|_{V_1}$
in
![]() $\mathcal {M}_d^{cm}$
. We repeat the argument with
$\mathcal {M}_d^{cm}$
. We repeat the argument with
![]() $\mathcal {Y}_1$
in place of
$\mathcal {Y}_1$
in place of
![]() $\mathcal {Y}$
. By maximal variation of
$\mathcal {Y}$
. By maximal variation of
![]() $\mathcal {X}$
, we know that
$\mathcal {X}$
, we know that
and
![]() $T_{\mathrm {bif}}^{\wedge k_1} \not =0$
on
$T_{\mathrm {bif}}^{\wedge k_1} \not =0$
on
![]() $\mathcal {Y}_1$
. We choose another collection of critical points
$\mathcal {Y}_1$
. We choose another collection of critical points
![]() $c_{2,1}, \ldots , c_{2,r+1} \in \{c_1, \ldots , c_k\}$
so that the first r are transversely prerepelling at
$c_{2,1}, \ldots , c_{2,r+1} \in \{c_1, \ldots , c_k\}$
so that the first r are transversely prerepelling at
![]() $y_0$
over
$y_0$
over
![]() $X_{\lambda _0}$
and the full
$X_{\lambda _0}$
and the full
![]() $(r+1)$
-tuple is transversely prerepelling at
$(r+1)$
-tuple is transversely prerepelling at
![]() $y_0$
over
$y_0$
over
![]() $\mathcal {Y}_1$
. Note that we could take
$\mathcal {Y}_1$
. Note that we could take
![]() $c_{2,j} = c_{1,j}$
for
$c_{2,j} = c_{1,j}$
for
![]() $j = 1, \ldots , r$
. We let
$j = 1, \ldots , r$
. We let
![]() $Z_2 \subset \mathcal {Y}_1$
be the codimension-
$Z_2 \subset \mathcal {Y}_1$
be the codimension-
![]() $(r+1)$
subvariety containing
$(r+1)$
subvariety containing
![]() $y_0$
where these critical points are persistently preperiodic. Then
$y_0$
where these critical points are persistently preperiodic. Then
![]() $\pi _2^{-1}(Z_2) \cap \pi _1^{-1}(Z_1)$
has codimension
$\pi _2^{-1}(Z_2) \cap \pi _1^{-1}(Z_1)$
has codimension
![]() $2(r+1)$
in
$2(r+1)$
in
![]() $\mathcal {Y}_\ell $
.
$\mathcal {Y}_\ell $
.
In this way, we inductively construct a parameter
![]() $y = (y_0, \ldots , y_0) \in \mathcal {Y}_\ell $
and an
$y = (y_0, \ldots , y_0) \in \mathcal {Y}_\ell $
and an
![]() $\ell (r+1)$
-tuple of marked critical points
$\ell (r+1)$
-tuple of marked critical points
which is transversely prerepelling for the map
![]() $\Phi $
at y over
$\Phi $
at y over
![]() $\mathcal {Y}_\ell $
. In particular, in the language of [Reference DeMarco and MavrakiDM1, §4.3], the graph
$\mathcal {Y}_\ell $
. In particular, in the language of [Reference DeMarco and MavrakiDM1, §4.3], the graph
![]() $\Gamma _{\mathbf {c}}$
of
$\Gamma _{\mathbf {c}}$
of
![]() $\mathbf {c}$
in
$\mathbf {c}$
in
![]() $\mathcal {Y}_\ell \times (\mathbb {P}^1)^{\ell (r+1)}$
defines a rigid repeller for the map
$\mathcal {Y}_\ell \times (\mathbb {P}^1)^{\ell (r+1)}$
defines a rigid repeller for the map
![]() $\Phi $
at this parameter, and we conclude from [Reference DeMarco and MavrakiDM1, Proposition 4.8] that
$\Phi $
at this parameter, and we conclude from [Reference DeMarco and MavrakiDM1, Proposition 4.8] that
where
 $$ \begin{align*}\hat{T}_\Phi = \sum_{i=1}^\ell \sum_{j = 1}^{r+1} p_{i,j}^* \hat{T}_{f_i}\end{align*} $$
$$ \begin{align*}\hat{T}_\Phi = \sum_{i=1}^\ell \sum_{j = 1}^{r+1} p_{i,j}^* \hat{T}_{f_i}\end{align*} $$
is the dynamical Green current for
![]() $\Phi $
on
$\Phi $
on
![]() $\Lambda \times (\mathbb {P}^1)^{\ell (r+1)}$
, for the projections
$\Lambda \times (\mathbb {P}^1)^{\ell (r+1)}$
, for the projections
![]() $p_{i,j}: \Lambda \times (\mathbb {P}^1)^{\ell (r+1)} \to \Lambda \times \mathbb {P}^1$
. Unwinding the definitions, we conclude that
$p_{i,j}: \Lambda \times (\mathbb {P}^1)^{\ell (r+1)} \to \Lambda \times \mathbb {P}^1$
. Unwinding the definitions, we conclude that
and therefore that
so that the measure
![]() $\mu _\ell \not =0$
. Here we used the fact that
$\mu _\ell \not =0$
. Here we used the fact that
![]() $\dim \mathcal {X}_V^{\ell }=\dim \mathcal {Y}_{\ell }$
from the maximal variation.
$\dim \mathcal {X}_V^{\ell }=\dim \mathcal {Y}_{\ell }$
from the maximal variation.
Finally, since the map from
![]() $\mathcal {X}_V^{\ell }$
to
$\mathcal {X}_V^{\ell }$
to
![]() $\mathcal {Y}_\ell $
is generically finite by Proposition 2.1, our initial choice of
$\mathcal {Y}_\ell $
is generically finite by Proposition 2.1, our initial choice of
![]() $y_0$
guarantees that the marked critical points
$y_0$
guarantees that the marked critical points
![]() $\mathbf {c}$
are also transversely prerepelling at a preimage of y, over
$\mathbf {c}$
are also transversely prerepelling at a preimage of y, over
![]() $\mathcal {X}_V^\ell $
.
$\mathcal {X}_V^\ell $
.
3.2 Measures on
 $\mathcal {X}_V^{\ell +1}$
$\mathcal {X}_V^{\ell +1}$
Let
![]() $\mu _\ell $
be the measure of Proposition 3.1, witnessed by the marked critical point
$\mu _\ell $
be the measure of Proposition 3.1, witnessed by the marked critical point
![]() $\mathbf {c}$
. We now use these critical points to construct nonvanishing measures on the next fiber power
$\mathbf {c}$
. We now use these critical points to construct nonvanishing measures on the next fiber power
![]() $\mathcal {X}_V^{\ell +1}$
. Let
$\mathcal {X}_V^{\ell +1}$
. Let
be as in Proposition 3.1 parameterized by
![]() $\mathcal {X}_V^\ell $
via the map
$\mathcal {X}_V^\ell $
via the map
![]() $\rho _{\ell }$
of (3.1), and let
$\rho _{\ell }$
of (3.1), and let
be the family of maps on
![]() $(\mathbb {P}^1)^{\ell (r+1)+r}$
parameterized by
$(\mathbb {P}^1)^{\ell (r+1)+r}$
parameterized by
![]() $\mathcal {X}_V^{\ell +1}$
, where
$\mathcal {X}_V^{\ell +1}$
, where
![]() $f_1, \ldots , f_{\ell }$
are each repeated
$f_1, \ldots , f_{\ell }$
are each repeated
![]() $r+1$
times, but the final coordinate
$r+1$
times, but the final coordinate
![]() $f_{\ell +1}$
is only repeated r times. Specializing at each
$f_{\ell +1}$
is only repeated r times. Specializing at each
![]() $\lambda \in V$
we also have a family of maps
$\lambda \in V$
we also have a family of maps
parametrized by
![]() $X_{\lambda } \subset \mathcal {M}_d^{cm}$
, and, focusing on the
$X_{\lambda } \subset \mathcal {M}_d^{cm}$
, and, focusing on the
![]() $\ell $
-th factor of
$\ell $
-th factor of
![]() $\mathcal {X}_V^\ell $
and associated components of
$\mathcal {X}_V^\ell $
and associated components of
![]() $\mathbf {c}$
, we will use the marked critical points
$\mathbf {c}$
, we will use the marked critical points
to define two measures
![]() $\mu _\ell ^i$
and
$\mu _\ell ^i$
and
![]() $\mu _\ell ^j$
on
$\mu _\ell ^j$
on
![]() $\mathcal {X}_V^{\ell +1}$
. Conditions (1) and (2) of Proposition 3.2 will allow us to conclude that
$\mathcal {X}_V^{\ell +1}$
. Conditions (1) and (2) of Proposition 3.2 will allow us to conclude that
![]() $\mu _\ell ^i$
and
$\mu _\ell ^i$
and
![]() $\mu _\ell ^j$
are nonzero. Conditions (3) and (4) will allow us to prove in Section 4 that
$\mu _\ell ^j$
are nonzero. Conditions (3) and (4) will allow us to prove in Section 4 that
![]() $\mu _\ell ^i$
and
$\mu _\ell ^i$
and
![]() $\mu _\ell ^j$
are not proportional measures.
$\mu _\ell ^j$
are not proportional measures.
Proposition 3.2. Suppose the marked critical point
witnesses
![]() $\mu _\ell \not =0$
on
$\mu _\ell \not =0$
on
![]() $\mathcal {X}_V^\ell $
. Then there are parameters
$\mathcal {X}_V^\ell $
. Then there are parameters
![]() $x_0 = (\lambda _0, t_1, \ldots , t_\ell )$
and
$x_0 = (\lambda _0, t_1, \ldots , t_\ell )$
and
![]() $x_1 = (\lambda _1, s_1, \ldots , s_\ell )$
in the support of
$x_1 = (\lambda _1, s_1, \ldots , s_\ell )$
in the support of
![]() $\mu _\ell $
in
$\mu _\ell $
in
![]() $\mathcal {X}_V^\ell $
and indices
$\mathcal {X}_V^\ell $
and indices
![]() $i \not = j$
in
$i \not = j$
in
![]() $\{1, \ldots , r+1\}$
so that
$\{1, \ldots , r+1\}$
so that
-
1. the r-tuple
 $(c_{\ell ,1}, \ldots , \widehat {c_{\ell , i}}, \ldots c_{\ell , r+1})$
is transversely prerepelling for
$(c_{\ell ,1}, \ldots , \widehat {c_{\ell , i}}, \ldots c_{\ell , r+1})$
is transversely prerepelling for
 $F^{(\lambda _0)}$
at
$F^{(\lambda _0)}$
at
 $t_\ell $
over
$t_\ell $
over
 $X_{\lambda _0}$
;
$X_{\lambda _0}$
; -
2. the r-tuple
 $(c_{\ell ,1}, \ldots , \widehat {c_{\ell , j}}, \ldots c_{\ell , r+1})$
is properly prerepelling for
$(c_{\ell ,1}, \ldots , \widehat {c_{\ell , j}}, \ldots c_{\ell , r+1})$
is properly prerepelling for
 $F^{(\lambda _0)}$
at
$F^{(\lambda _0)}$
at
 $t_\ell $
over
$t_\ell $
over
 $X_{\lambda _0}$
;
$X_{\lambda _0}$
; -
3. the r-tuple
 $(c_{\ell ,1}, \ldots , \widehat {c_{\ell , i}}, \ldots c_{\ell , r+1})$
is transversely prerepelling for
$(c_{\ell ,1}, \ldots , \widehat {c_{\ell , i}}, \ldots c_{\ell , r+1})$
is transversely prerepelling for
 $F^{(\lambda _1)}$
at
$F^{(\lambda _1)}$
at
 $s_\ell $
over
$s_\ell $
over
 $X_{\lambda _1}$
; and
$X_{\lambda _1}$
; and -
4. the critical point
 $c_{\ell , i}$
is attracted to a parabolic periodic point of f at
$c_{\ell , i}$
is attracted to a parabolic periodic point of f at
 $s_\ell \in X_{\lambda _1}$
,
$s_\ell \in X_{\lambda _1}$
,
where
![]() $\widehat {c_{\ell , i}}$
means that the i-th coordinate is omitted. Let
$\widehat {c_{\ell , i}}$
means that the i-th coordinate is omitted. Let
![]() $\Pi _1:\mathcal {X}^{\ell }_V \times _V \mathcal {X}\to \mathcal {X}_V^\ell $
and
$\Pi _1:\mathcal {X}^{\ell }_V \times _V \mathcal {X}\to \mathcal {X}_V^\ell $
and
![]() $\Pi _2:\mathcal {X}_V^{\ell }\times _V\mathcal {X}\to \mathcal {X}$
. Then
$\Pi _2:\mathcal {X}_V^{\ell }\times _V\mathcal {X}\to \mathcal {X}$
. Then
and
on
![]() $\mathcal {X}_V^{\ell +1}$
.
$\mathcal {X}_V^{\ell +1}$
.
Proof. Via the map
![]() $\rho _\ell : \mathcal {X}_V^{\ell } \to (\mathcal {M}_d^{cm})^{\ell }$
, we view
$\rho _\ell : \mathcal {X}_V^{\ell } \to (\mathcal {M}_d^{cm})^{\ell }$
, we view
![]() $\mathcal {X}_V^{\ell }$
as the parameter space for a family of product maps
$\mathcal {X}_V^{\ell }$
as the parameter space for a family of product maps
![]() $\Phi = (f_1, \ldots , f_1, \ldots , f_\ell , \ldots , f_\ell )$
on
$\Phi = (f_1, \ldots , f_1, \ldots , f_\ell , \ldots , f_\ell )$
on
![]() $(\mathbb {P}^1)^{\ell (r+1)}$
. From Proposition 3.1, we know that
$(\mathbb {P}^1)^{\ell (r+1)}$
. From Proposition 3.1, we know that
![]() $\mathbf {c}$
is transversely prerepelling for
$\mathbf {c}$
is transversely prerepelling for
![]() $\Phi $
at a parameter
$\Phi $
at a parameter
![]() $x_0 = (\lambda _0, t_1, \ldots , t_\ell ) \in \operatorname {supp} \mu _\ell $
.
$x_0 = (\lambda _0, t_1, \ldots , t_\ell ) \in \operatorname {supp} \mu _\ell $
.
Let
![]() $S_{i,j}$
be the irreducible component of the hypersurface in
$S_{i,j}$
be the irreducible component of the hypersurface in
![]() $\mathcal {X}_V^\ell $
containing
$\mathcal {X}_V^\ell $
containing
![]() $x_0$
along which
$x_0$
along which
![]() $c_{i,j}$
is persistently preperiodic for
$c_{i,j}$
is persistently preperiodic for
![]() $f_i$
,
$f_i$
,
![]() $i = 1, \ldots , \ell $
,
$i = 1, \ldots , \ell $
,
![]() $j = 1, \ldots , r+1$
. Consider the component of the intersection
$j = 1, \ldots , r+1$
. Consider the component of the intersection
containing
![]() $x_0$
in
$x_0$
in
![]() $\mathcal {X}_V^\ell $
. Similar to the proof of Proposition 2.1, for dimension reasons, it maps (generically finitely) to a family
$\mathcal {X}_V^\ell $
. Similar to the proof of Proposition 2.1, for dimension reasons, it maps (generically finitely) to a family
![]() $\mathcal {X}_1 \to V_1$
of r-dimensional varieties over a 1-dimensional base, where these marked critical points are persistently preperiodic for
$\mathcal {X}_1 \to V_1$
of r-dimensional varieties over a 1-dimensional base, where these marked critical points are persistently preperiodic for
![]() $f_1, \ldots , f_{\ell -1}$
. We will continue to write
$f_1, \ldots , f_{\ell -1}$
. We will continue to write
![]() $x_0 = (\lambda _0, t_\ell )$
for the point we started with, but now viewed in
$x_0 = (\lambda _0, t_\ell )$
for the point we started with, but now viewed in
![]() $\mathcal {X}_1$
.
$\mathcal {X}_1$
.
By the transversality, we know that r of the remaining critical points, say
![]() $c_{\ell ,1}, \ldots , c_{\ell , r}$
, are transversely prerepelling at
$c_{\ell ,1}, \ldots , c_{\ell , r}$
, are transversely prerepelling at
![]() $t_\ell $
for
$t_\ell $
for
![]() $F^{(\lambda _0)} = (f, f, \ldots , f)$
over
$F^{(\lambda _0)} = (f, f, \ldots , f)$
over
![]() $X_{\lambda _0}$
.
$X_{\lambda _0}$
.
We now aim to show that by modifying the parameter
![]() $x_0$
if necessary, we can arrange so that another r-tuple, say
$x_0$
if necessary, we can arrange so that another r-tuple, say
![]() $c_{\ell , 2}, \ldots , c_{\ell , r+1}$
, is also properly prerepelling at
$c_{\ell , 2}, \ldots , c_{\ell , r+1}$
, is also properly prerepelling at
![]() $t_\ell $
for
$t_\ell $
for
![]() $F^{(\lambda _0)}$
over
$F^{(\lambda _0)}$
over
![]() $X_{\lambda _0}$
. Note that transversality of the intersection
$X_{\lambda _0}$
. Note that transversality of the intersection
![]() $S_{1,1} \cap \cdots \cap S_{\ell -1, r+1}$
at the original
$S_{1,1} \cap \cdots \cap S_{\ell -1, r+1}$
at the original
![]() $x_0$
persists in a neighborhood, so the first
$x_0$
persists in a neighborhood, so the first
![]() $(\ell -1)(r+1)$
critical points remain transversely prerepelling in a neighborhood of
$(\ell -1)(r+1)$
critical points remain transversely prerepelling in a neighborhood of
![]() $x_0$
for
$x_0$
for
![]() $(f_1, \ldots , f_{\ell -1})$
.
$(f_1, \ldots , f_{\ell -1})$
.
Consider the intersection
in
![]() $\mathcal {X}_1$
. These hypersurfaces intersect transversely at
$\mathcal {X}_1$
. These hypersurfaces intersect transversely at
![]() $x_0$
and so define a smooth holomorphic curve
$x_0$
and so define a smooth holomorphic curve
![]() $\Gamma $
containing
$\Gamma $
containing
![]() $x_0$
which is locally a section of
$x_0$
which is locally a section of
![]() $\mathcal {X}_1 \to V_1$
near
$\mathcal {X}_1 \to V_1$
near
![]() $\lambda _0$
. The intersection of
$\lambda _0$
. The intersection of
![]() $\Gamma $
with
$\Gamma $
with
![]() $X_{\lambda _0}$
is
$X_{\lambda _0}$
is
![]() $x_0 = (\lambda _0, t_\ell )$
. Note further that
$x_0 = (\lambda _0, t_\ell )$
. Note further that
![]() $c_{\ell , r+1}$
is not persistently preperiodic along
$c_{\ell , r+1}$
is not persistently preperiodic along
![]() $\Gamma $
(because of the original setup of transverse intersections), and so
$\Gamma $
(because of the original setup of transverse intersections), and so
![]() $c_{\ell , r+1}$
must be active along
$c_{\ell , r+1}$
must be active along
![]() $\Gamma $
with
$\Gamma $
with
![]() $x_0$
in its bifurcation locus (because it lands at a repelling cycle there). The bifurcation locus for
$x_0$
in its bifurcation locus (because it lands at a repelling cycle there). The bifurcation locus for
![]() $c_{\ell ,r+1}$
in
$c_{\ell ,r+1}$
in
![]() $\Gamma $
has no isolated points, so there must be an infinite collection of parameters
$\Gamma $
has no isolated points, so there must be an infinite collection of parameters
![]() $x \in \Gamma $
where
$x \in \Gamma $
where
![]() $c_{\ell , r+1}$
is preperiodic to a repelling cycle for
$c_{\ell , r+1}$
is preperiodic to a repelling cycle for
![]() $f_\ell $
, dense in the bifurcation locus of
$f_\ell $
, dense in the bifurcation locus of
![]() $c_{\ell , r+1}$
in a neighborhood of
$c_{\ell , r+1}$
in a neighborhood of
![]() $x_0$
.
$x_0$
.
Now omit
![]() $S_{\ell , 1}$
from the intersection, so that
$S_{\ell , 1}$
from the intersection, so that
![]() $S_{\ell ,2} \cap \cdots \cap S_{\ell , r}$
(in
$S_{\ell ,2} \cap \cdots \cap S_{\ell , r}$
(in
![]() $\mathcal {X}_1$
) defines a 1-parameter family of algebraic curves
$\mathcal {X}_1$
) defines a 1-parameter family of algebraic curves
![]() $\mathcal {C}$
, for all
$\mathcal {C}$
, for all
![]() $\lambda $
in a small neighborhood of
$\lambda $
in a small neighborhood of
![]() $\lambda _0\in V_1$
, by
$\lambda _0\in V_1$
, by
We know that
![]() $S_{\ell , r+1}$
intersects the total space of this family
$S_{\ell , r+1}$
intersects the total space of this family
![]() $\mathcal {C}$
transversely at the given point
$\mathcal {C}$
transversely at the given point
![]() $x_0$
. Suppose that it fails to intersect properly when restricted to
$x_0$
. Suppose that it fails to intersect properly when restricted to
![]() $X_{\lambda _0}$
; this would mean that
$X_{\lambda _0}$
; this would mean that
![]() $c_{\ell , r+1}$
is persistently preperiodic along the curve
$c_{\ell , r+1}$
is persistently preperiodic along the curve
![]() $C_{\lambda _0}$
in
$C_{\lambda _0}$
in
![]() $X_{\lambda _0}$
. Suppose this happens at all parameters
$X_{\lambda _0}$
. Suppose this happens at all parameters
![]() $x \in \Gamma $
where
$x \in \Gamma $
where
![]() $c_{\ell , r+1}$
is preperiodic to a repelling cycle. This implies that the associated bifurcation current
$c_{\ell , r+1}$
is preperiodic to a repelling cycle. This implies that the associated bifurcation current
![]() $T_{c_{\ell , r+1}}$
vanishes identically on each of these curves
$T_{c_{\ell , r+1}}$
vanishes identically on each of these curves
![]() $C_x$
passing through each such x in the family
$C_x$
passing through each such x in the family
![]() $\mathcal {C}$
. By continuity of potentials of the bifurcation currents, we deduce that
$\mathcal {C}$
. By continuity of potentials of the bifurcation currents, we deduce that
![]() $T_{c_{\ell , r+1}}$
vanishes along
$T_{c_{\ell , r+1}}$
vanishes along
![]() $C_x$
for all x in
$C_x$
for all x in
![]() $\operatorname {supp} T_{c_{\ell , r+1}}|_\Gamma $
near
$\operatorname {supp} T_{c_{\ell , r+1}}|_\Gamma $
near
![]() $x_0$
. But this means that
$x_0$
. But this means that
![]() $c_{\ell , r+1}$
is persistently preperiodic along each of these curves [Reference Dujardin and FavreDF, Theorem 2.5]. As they form an uncountable family, we see that
$c_{\ell , r+1}$
is persistently preperiodic along each of these curves [Reference Dujardin and FavreDF, Theorem 2.5]. As they form an uncountable family, we see that
![]() $c_{\ell , r+1}$
must be preperiodic along the entire family
$c_{\ell , r+1}$
must be preperiodic along the entire family
![]() $\mathcal {C}$
, which is a contradiction.
$\mathcal {C}$
, which is a contradiction.
We conclude that we can adjust our parameter
![]() $\lambda _0$
slightly, if needed, so that points
$\lambda _0$
slightly, if needed, so that points
![]() $c_{\ell , 1}, \ldots , c_{\ell , r}$
are transversely prerepelling at a new choice of
$c_{\ell , 1}, \ldots , c_{\ell , r}$
are transversely prerepelling at a new choice of
![]() $x_0 \in \Gamma $
along
$x_0 \in \Gamma $
along
![]() $X_{\lambda _0}$
while
$X_{\lambda _0}$
while
![]() $c_{\ell , 2}, \ldots , c_{\ell , r+1}$
are properly prerepelling at
$c_{\ell , 2}, \ldots , c_{\ell , r+1}$
are properly prerepelling at
![]() $x_0$
along
$x_0$
along
![]() $X_{\lambda _0}$
. This completes the proofs of (1) and (2) of the proposition.
$X_{\lambda _0}$
. This completes the proofs of (1) and (2) of the proposition.
As
![]() $c_{\ell ,r+1}$
is bifurcating along the curve we called
$c_{\ell ,r+1}$
is bifurcating along the curve we called
![]() $\Gamma $
, the characterizations of J-stability (as in [Reference Mañé, Sad and SullivanMSS]) imply that there are parameters, everywhere dense in its bifurcation locus, for which the maps have a parabolic cycle; the theory of renormalization (see [Reference Douady and Hamal HubbardDH1]) implies that
$\Gamma $
, the characterizations of J-stability (as in [Reference Mañé, Sad and SullivanMSS]) imply that there are parameters, everywhere dense in its bifurcation locus, for which the maps have a parabolic cycle; the theory of renormalization (see [Reference Douady and Hamal HubbardDH1]) implies that
![]() $c_{\ell , r+1}$
will lie in the basin of the parabolic cycle. We let
$c_{\ell , r+1}$
will lie in the basin of the parabolic cycle. We let
![]() $\lambda _1$
be a parameter close to
$\lambda _1$
be a parameter close to
![]() $\lambda _0$
in the support of
$\lambda _0$
in the support of
![]() $\pi _* \mu _\ell $
, where
$\pi _* \mu _\ell $
, where
![]() $\pi $
is the projection to V, so that
$\pi $
is the projection to V, so that
![]() $c_{\ell ,r+1}$
is attracted to a parabolic cycle at
$c_{\ell ,r+1}$
is attracted to a parabolic cycle at
![]() $x_1 := \Gamma \cap X_{\lambda _1}$
, while
$x_1 := \Gamma \cap X_{\lambda _1}$
, while
![]() $c_{\ell ,1}, \ldots , c_{\ell ,r}$
remain transversely prerepelling at
$c_{\ell ,1}, \ldots , c_{\ell ,r}$
remain transversely prerepelling at
![]() $x_1$
along
$x_1$
along
![]() $X_{\lambda _1}$
. This completes the proof of properties (1)–(4).
$X_{\lambda _1}$
. This completes the proof of properties (1)–(4).
To prove the non-vanishing of
![]() $\mu _\ell ^i$
and
$\mu _\ell ^i$
and
![]() $\mu _\ell ^j$
, consider the map
$\mu _\ell ^j$
, consider the map
![]() $\Phi _{\ell +1} = f_1^{\times (r+1)} \times \cdots \times f_{\ell }^{\times (r+1)}\times f_{\ell +1}^{\times r}$
on
$\Phi _{\ell +1} = f_1^{\times (r+1)} \times \cdots \times f_{\ell }^{\times (r+1)}\times f_{\ell +1}^{\times r}$
on
![]() $(\mathbb {P}^1)^{\ell (r+1) + r}$
over
$(\mathbb {P}^1)^{\ell (r+1) + r}$
over
![]() $\mathcal {X}_V^{\ell +1}$
. The argument above, leading to properties (1) and (2), shows that we can label critical points of
$\mathcal {X}_V^{\ell +1}$
. The argument above, leading to properties (1) and (2), shows that we can label critical points of
![]() $f_1, \ldots , f_{\ell +1}$
so that the graphs of the marked points
$f_1, \ldots , f_{\ell +1}$
so that the graphs of the marked points
and
each define a rigid repeller for the map
![]() $\Phi _{\ell +1}$
over a neighborhood of a parameter
$\Phi _{\ell +1}$
over a neighborhood of a parameter
![]() $(\lambda _0, t_1, \ldots , t_\ell , t_\ell )$
in
$(\lambda _0, t_1, \ldots , t_\ell , t_\ell )$
in
![]() $\mathcal {X}_V^{\ell +1}$
, in the sense of [Reference DeMarco and MavrakiDM1, §4.3], and so the measures are nonzero by [Reference DeMarco and MavrakiDM1, Proposition 4.8].
$\mathcal {X}_V^{\ell +1}$
, in the sense of [Reference DeMarco and MavrakiDM1, §4.3], and so the measures are nonzero by [Reference DeMarco and MavrakiDM1, Proposition 4.8].
4 Proof of Theorem 1.8
Suppose that
![]() $\mathcal {X}\to V$
is a maximally varying family of r-dimensional varieties
$\mathcal {X}\to V$
is a maximally varying family of r-dimensional varieties
![]() $X_{\lambda }\subset M_d$
parametrized by V of dimension
$X_{\lambda }\subset M_d$
parametrized by V of dimension
![]() $\ell \ge 1$
, defined over
$\ell \ge 1$
, defined over
![]() $\overline {\mathbb {Q}}$
. As in §2.1, we may pass to a finite branched cover
$\overline {\mathbb {Q}}$
. As in §2.1, we may pass to a finite branched cover
![]() $\mathcal {M}_d^{cm} \to \mathrm {M}_d$
over which we can define a family of maps
$\mathcal {M}_d^{cm} \to \mathrm {M}_d$
over which we can define a family of maps
![]() $f:\mathbb {P}^1 \to \mathbb {P}^1$
with
$f:\mathbb {P}^1 \to \mathbb {P}^1$
with
![]() $2d-2$
marked critical points. Pulling back each
$2d-2$
marked critical points. Pulling back each
![]() $X_\lambda $
and possibly replacing V with a finite branched cover, we will continue to use the notation
$X_\lambda $
and possibly replacing V with a finite branched cover, we will continue to use the notation
![]() $\mathcal {X} \to V$
for the family of varieties in
$\mathcal {X} \to V$
for the family of varieties in
![]() $\mathcal {M}_d^{cm}$
. Therefore, we may assume that we can define the family of product maps
$\mathcal {M}_d^{cm}$
. Therefore, we may assume that we can define the family of product maps
on
![]() $(\mathbb {P}^1)^{(r+1)\ell }$
, parametrized by
$(\mathbb {P}^1)^{(r+1)\ell }$
, parametrized by
![]() $\mathcal {X}^{\ell }_V$
and defined over
$\mathcal {X}^{\ell }_V$
and defined over
![]() $\overline {\mathbb {Q}}$
, where each coordinate
$\overline {\mathbb {Q}}$
, where each coordinate
![]() $f_i$
is repeated
$f_i$
is repeated
![]() $r+1$
times and a family
$r+1$
times and a family
on
![]() $(\mathbb {P}^1)^{r}$
, parametrized by
$(\mathbb {P}^1)^{r}$
, parametrized by
![]() $\mathcal {X}$
, where each coordinate is repeated r times. We denote by
$\mathcal {X}$
, where each coordinate is repeated r times. We denote by
![]() $\overline {L}_{\Phi }$
and
$\overline {L}_{\Phi }$
and
![]() $\overline {L}_{\Phi _{(\ell +1)}}$
the
$\overline {L}_{\Phi _{(\ell +1)}}$
the
![]() $\Phi $
(respectively
$\Phi $
(respectively
![]() $\Phi _{(\ell +1)}$
)-invariant extension of the classical polarization as defined by [Reference Yuan and ZhangYZ, Theorem 6.1.1]. In particular, using the notation in [Reference Yuan and ZhangYZ], we have that
$\Phi _{(\ell +1)}$
)-invariant extension of the classical polarization as defined by [Reference Yuan and ZhangYZ, Theorem 6.1.1]. In particular, using the notation in [Reference Yuan and ZhangYZ], we have that
![]() $\overline {L}_{\Phi _{(\ell +1)}}\in \widehat {\mathrm {Pic}}(\mathcal {X}\times (\mathbb {P}^1)^r)_{\mathbb {Q},\mathrm {nef}}$
and
$\overline {L}_{\Phi _{(\ell +1)}}\in \widehat {\mathrm {Pic}}(\mathcal {X}\times (\mathbb {P}^1)^r)_{\mathbb {Q},\mathrm {nef}}$
and
![]() $\overline {L}_{\Phi }\in \widehat {\mathrm {Pic}}(\mathcal {X}^{\ell }_V\times (\mathbb {P}^1)^{\dim \mathcal {X}^{\ell }_V})_{\mathbb {Q},\mathrm {nef}}$
.
$\overline {L}_{\Phi }\in \widehat {\mathrm {Pic}}(\mathcal {X}^{\ell }_V\times (\mathbb {P}^1)^{\dim \mathcal {X}^{\ell }_V})_{\mathbb {Q},\mathrm {nef}}$
.
In what follows it is convenient to work with the Deligne pairing (of relative dimension
![]() $0$
), of the invariant metrized line bundles restricted to graphs of critical marked points (see [Reference Yuan and ZhangYZ, §4.2] for metrics of the Deligne pairing and [Reference Yuan and ZhangYZ, §6.2.2] for the “restriction” of the invariant metrized line bundle to a subvariety). By [Reference Yuan and ZhangYZ, Theorem 4.2.3], to each marked tuple of critical points
$0$
), of the invariant metrized line bundles restricted to graphs of critical marked points (see [Reference Yuan and ZhangYZ, §4.2] for metrics of the Deligne pairing and [Reference Yuan and ZhangYZ, §6.2.2] for the “restriction” of the invariant metrized line bundle to a subvariety). By [Reference Yuan and ZhangYZ, Theorem 4.2.3], to each marked tuple of critical points
![]() $\mathbf {c}: \mathcal {X}^{\ell }_V\to (\mathbb {P}^1)^{\dim \mathcal {X}^{\ell }_V}$
we can associate a metrized line bundle
$\mathbf {c}: \mathcal {X}^{\ell }_V\to (\mathbb {P}^1)^{\dim \mathcal {X}^{\ell }_V}$
we can associate a metrized line bundle
![]() $\langle \overline {L}_{\Phi }|_{\Gamma _{\mathbf {c}}}\rangle \in \widehat {\mathrm {Pic}}( \mathcal {X}^{\ell }_V)_{\mathbb {Q},\mathrm {nef}}$
, where
$\langle \overline {L}_{\Phi }|_{\Gamma _{\mathbf {c}}}\rangle \in \widehat {\mathrm {Pic}}( \mathcal {X}^{\ell }_V)_{\mathbb {Q},\mathrm {nef}}$
, where
![]() $\Gamma _{\mathbf {c}}$
denotes the graph of
$\Gamma _{\mathbf {c}}$
denotes the graph of
![]() $\mathbf {c}$
in
$\mathbf {c}$
in
![]() $\mathcal {X}^{\ell }_V\times (\mathbb {P}^1)^{\dim \mathcal {X}^{\ell }_V}$
. Moreover, we let
$\mathcal {X}^{\ell }_V\times (\mathbb {P}^1)^{\dim \mathcal {X}^{\ell }_V}$
. Moreover, we let
be the tensor product over all marked tuples of critical points
![]() $\mathbf {c}$
for the maps
$\mathbf {c}$
for the maps
![]() $f_1, \ldots , f_\ell $
.
$f_1, \ldots , f_\ell $
.
Now let
![]() $\mathbf {c}=(c_{1,1},\ldots ,c_{\ell ,r+1}):\mathcal {X}^{\ell }_{V}\to (\mathbb {P}^1)^{(r+1)\ell }$
be a marked critical point for
$\mathbf {c}=(c_{1,1},\ldots ,c_{\ell ,r+1}):\mathcal {X}^{\ell }_{V}\to (\mathbb {P}^1)^{(r+1)\ell }$
be a marked critical point for
![]() $\Phi $
that witnesses
$\Phi $
that witnesses
![]() $\mu _{\ell } \not =0$
, as in Proposition 3.1. Reordering the critical points if needed, we can find
$\mu _{\ell } \not =0$
, as in Proposition 3.1. Reordering the critical points if needed, we can find
![]() $x_0,x_1\in \operatorname {supp}\mu _{\ell }$
as in Proposition 3.2, with
$x_0,x_1\in \operatorname {supp}\mu _{\ell }$
as in Proposition 3.2, with
![]() $i=r+1$
and
$i=r+1$
and
![]() $j=1$
. We write
$j=1$
. We write
![]() $c_i:=c_{\ell ,i}:\mathcal {X}\to \mathbb {P}^1$
in what follows. As before, using [Reference Yuan and ZhangYZ, Theorem 4.2.3], we define two adelic metrized line bundles on
$c_i:=c_{\ell ,i}:\mathcal {X}\to \mathbb {P}^1$
in what follows. As before, using [Reference Yuan and ZhangYZ, Theorem 4.2.3], we define two adelic metrized line bundles on
![]() $\mathcal {X}$
by
$\mathcal {X}$
by
 $$ \begin{align} \begin{split} \overline{L}_1&:=\langle\overline{L}_{\Phi_{(\ell+1)}}|_{\Gamma_{(c_1,\ldots,c_r)}}\rangle\in \widehat{\mathrm{Pic}}( \mathcal{X})_{\mathbb{Q},\mathrm{nef}}\\ \overline{L}_2&:=\langle\overline{L}_{\Phi_{(\ell+1)}}|_{\Gamma_{(c_2,\ldots,c_{r+1})}}\rangle\in \widehat{\mathrm{Pic}}( \mathcal{X})_{\mathbb{Q},\mathrm{nef}}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \overline{L}_1&:=\langle\overline{L}_{\Phi_{(\ell+1)}}|_{\Gamma_{(c_1,\ldots,c_r)}}\rangle\in \widehat{\mathrm{Pic}}( \mathcal{X})_{\mathbb{Q},\mathrm{nef}}\\ \overline{L}_2&:=\langle\overline{L}_{\Phi_{(\ell+1)}}|_{\Gamma_{(c_2,\ldots,c_{r+1})}}\rangle\in \widehat{\mathrm{Pic}}( \mathcal{X})_{\mathbb{Q},\mathrm{nef}}, \end{split} \end{align} $$
and note that their curvature forms (at an archimedean place) are the bifurcation currents
 $$ \begin{align} \begin{split} c_1(\overline{L}_1)&=T_{f_{\ell+1},c_1}+\cdots+T_{f_{\ell+1},c_r}\\ c_1(\overline{L}_2)&=T_{f_{\ell+1},c_2}+\cdots+T_{f_{\ell+1}, c_{r+1}}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} c_1(\overline{L}_1)&=T_{f_{\ell+1},c_1}+\cdots+T_{f_{\ell+1},c_r}\\ c_1(\overline{L}_2)&=T_{f_{\ell+1},c_2}+\cdots+T_{f_{\ell+1}, c_{r+1}}. \end{split} \end{align} $$
We can now define two metrized line bundles
on
![]() $\mathcal {X}^{\ell +1}_V$
for
$\mathcal {X}^{\ell +1}_V$
for
![]() $i=1,2$
. By [Reference Yuan and ZhangYZ, Lemma 6.2.1, Theorem 4.1.3], the heights associated to
$i=1,2$
. By [Reference Yuan and ZhangYZ, Lemma 6.2.1, Theorem 4.1.3], the heights associated to
![]() $\overline {M}_i$
vanish at PCF points; see also [Reference Yuan and ZhangYZ, Lemma 6.3.2]. More precisely, for a point
$\overline {M}_i$
vanish at PCF points; see also [Reference Yuan and ZhangYZ, Lemma 6.3.2]. More precisely, for a point
![]() $(\lambda _0,t_1,\ldots ,t_{\ell +1})\in \mathcal {X}^{\ell +1}_V(\overline {\mathbb {Q}})$
we have
$(\lambda _0,t_1,\ldots ,t_{\ell +1})\in \mathcal {X}^{\ell +1}_V(\overline {\mathbb {Q}})$
we have
 $$ \begin{align} \begin{split} h_{\overline{M}_1}(\lambda_0,t_1,\ldots,t_{\ell+1})&= \sum_{i=1}^{\ell}h_{\mathrm{crit}}(f_{i}) + \sum_{j=1}^{r}\hat{h}_{f_{\lambda_0,t_{\ell+1}}}(c_{j}(\lambda_0,t_{\ell+1}))\\ h_{\overline{M}_2}(\lambda_0,t_1,\ldots,t_{\ell+1})&= \sum_{i=1}^{\ell}h_{\mathrm{crit}}(f_{i}) + \sum_{j=2}^{r+1}\hat{h}_{f_{\lambda_0,t_{\ell+1}}}(c_{j}(\lambda_0,t_{\ell+1})). \end{split} \end{align} $$
$$ \begin{align} \begin{split} h_{\overline{M}_1}(\lambda_0,t_1,\ldots,t_{\ell+1})&= \sum_{i=1}^{\ell}h_{\mathrm{crit}}(f_{i}) + \sum_{j=1}^{r}\hat{h}_{f_{\lambda_0,t_{\ell+1}}}(c_{j}(\lambda_0,t_{\ell+1}))\\ h_{\overline{M}_2}(\lambda_0,t_1,\ldots,t_{\ell+1})&= \sum_{i=1}^{\ell}h_{\mathrm{crit}}(f_{i}) + \sum_{j=2}^{r+1}\hat{h}_{f_{\lambda_0,t_{\ell+1}}}(c_{j}(\lambda_0,t_{\ell+1})). \end{split} \end{align} $$
We will now show that
![]() $\overline {M}_i$
is “non-degenerate” for
$\overline {M}_i$
is “non-degenerate” for
![]() $i=1,2$
in the terminology of [Reference Yuan and ZhangYZ, §6.2.2]. Equivalently, by [Reference Yuan and ZhangYZ, Lemma 5.4], it suffices to show that
$i=1,2$
in the terminology of [Reference Yuan and ZhangYZ, §6.2.2]. Equivalently, by [Reference Yuan and ZhangYZ, Lemma 5.4], it suffices to show that
Recall that
![]() $T_{f_i,c_j}^{\wedge 2}=0$
for all
$T_{f_i,c_j}^{\wedge 2}=0$
for all
![]() $i,j$
and similarly
$i,j$
and similarly
![]() $(\Pi ^*_2c_1(\overline {L}_i))^{\wedge r+1}= (\Pi _2)^*(c_1(\overline {L}_i)^{\wedge r+1})=0$
for
$(\Pi ^*_2c_1(\overline {L}_i))^{\wedge r+1}= (\Pi _2)^*(c_1(\overline {L}_i)^{\wedge r+1})=0$
for
![]() $i=1,2$
, by the definition of the bifurcation current as limits of pullbacks, because the map
$i=1,2$
, by the definition of the bifurcation current as limits of pullbacks, because the map
![]() $\Phi _{(\ell +1)}$
acts on the r-dimensional
$\Phi _{(\ell +1)}$
acts on the r-dimensional
![]() $(\mathbb {P}^1)^{r}$
. Moreover, since
$(\mathbb {P}^1)^{r}$
. Moreover, since
![]() $\dim \mathcal {X}^{\ell }_V= \ell (r+1)$
we also have that
$\dim \mathcal {X}^{\ell }_V= \ell (r+1)$
we also have that
![]() $\Pi _1^{*}(c_1(\overline {L}))^{\wedge \ell (r+1)+1}=0$
. Thus, using also [Reference Yuan and ZhangYZ, Theorem 4.2.3] as before, we have
$\Pi _1^{*}(c_1(\overline {L}))^{\wedge \ell (r+1)+1}=0$
. Thus, using also [Reference Yuan and ZhangYZ, Theorem 4.2.3] as before, we have
on
![]() $\mathcal {X}_V^\ell $
, and
$\mathcal {X}_V^\ell $
, and
 $$ \begin{align} \begin{aligned} c_1(\overline{M_1})^{\wedge \ell(r+1)+r}&=\alpha_2\, \Pi_1^{*}(\mu_{\ell})\wedge \Pi_2^{*}(T_{f_{\ell+1},c_1}\wedge\cdots\wedge T_{f_{\ell+1},c_r})=\alpha_2\,\mu_{\ell}^{r+1}\neq 0,\\ c_1(\overline{M_2})^{\wedge \ell(r+1)+r}&=\alpha_3\,\Pi_1^{*}(\mu_{\ell})\wedge \Pi_2^{*}(T_{f_{\ell+1},c_2}\wedge\cdots\wedge T_{f_{\ell+1},c_{r+1}})=\alpha_3\,\mu^1_{\ell}\neq 0, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} c_1(\overline{M_1})^{\wedge \ell(r+1)+r}&=\alpha_2\, \Pi_1^{*}(\mu_{\ell})\wedge \Pi_2^{*}(T_{f_{\ell+1},c_1}\wedge\cdots\wedge T_{f_{\ell+1},c_r})=\alpha_2\,\mu_{\ell}^{r+1}\neq 0,\\ c_1(\overline{M_2})^{\wedge \ell(r+1)+r}&=\alpha_3\,\Pi_1^{*}(\mu_{\ell})\wedge \Pi_2^{*}(T_{f_{\ell+1},c_2}\wedge\cdots\wedge T_{f_{\ell+1},c_{r+1}})=\alpha_3\,\mu^1_{\ell}\neq 0, \end{aligned} \end{align} $$
for positive constants
![]() $\alpha _1,\alpha _2,\alpha _3>0$
. Their non-vanishing follows by Proposition 3.2 (and our choice of critical points). Therefore, by the height inequality [Reference Yuan and ZhangYZ, Theorem 1.3.2] we infer that there are positive constants
$\alpha _1,\alpha _2,\alpha _3>0$
. Their non-vanishing follows by Proposition 3.2 (and our choice of critical points). Therefore, by the height inequality [Reference Yuan and ZhangYZ, Theorem 1.3.2] we infer that there are positive constants
![]() $\epsilon _1=\epsilon _1(\mathcal {X})>0,~\epsilon _2=\epsilon _2(\mathcal {X})>0$
such that
$\epsilon _1=\epsilon _1(\mathcal {X})>0,~\epsilon _2=\epsilon _2(\mathcal {X})>0$
such that
 $$ \begin{align} \sum_{i=1}^{\ell+1}\hat{h}_{\mathrm{crit}}(f_i)\ge \epsilon_1 h_{\mathrm{Ch}}(\lambda)-\epsilon_2, \end{align} $$
$$ \begin{align} \sum_{i=1}^{\ell+1}\hat{h}_{\mathrm{crit}}(f_i)\ge \epsilon_1 h_{\mathrm{Ch}}(\lambda)-\epsilon_2, \end{align} $$
for all
![]() $(\lambda ,f_1,\ldots ,f_{\ell +1})\in U(\overline {\mathbb {Q}})$
for a Zariski open and dense subset
$(\lambda ,f_1,\ldots ,f_{\ell +1})\in U(\overline {\mathbb {Q}})$
for a Zariski open and dense subset
![]() $U\subset \mathcal {X}^{\ell +1}_V$
.
$U\subset \mathcal {X}^{\ell +1}_V$
.
It remains to show that for some
![]() $\epsilon =\epsilon (\mathcal {X})$
, the set
$\epsilon =\epsilon (\mathcal {X})$
, the set
 $$ \begin{align*}\left\{(\lambda,f_1,\ldots,f_{\ell+1})\in \mathcal{X}_V^{\ell+1}(\overline{\mathbb{Q}})~:~ \sum_{i=1}^{\ell+1}\hat{h}_{\mathrm{crit}}(f_i)<\epsilon\right\}\end{align*} $$
$$ \begin{align*}\left\{(\lambda,f_1,\ldots,f_{\ell+1})\in \mathcal{X}_V^{\ell+1}(\overline{\mathbb{Q}})~:~ \sum_{i=1}^{\ell+1}\hat{h}_{\mathrm{crit}}(f_i)<\epsilon\right\}\end{align*} $$
is not Zariski dense in
![]() $\mathcal {X}_V^{\ell +1}$
. We prove this result by contradiction. Suppose that there is a generic Galois invariant sequence
$\mathcal {X}_V^{\ell +1}$
. We prove this result by contradiction. Suppose that there is a generic Galois invariant sequence
![]() $\{x_n\}_n$
of critically small points in
$\{x_n\}_n$
of critically small points in
![]() $\mathcal {X}_V^{\ell +1}$
, so that
$\mathcal {X}_V^{\ell +1}$
, so that
![]() $h_{\overline {M}_i}(x_n)\to 0$
for
$h_{\overline {M}_i}(x_n)\to 0$
for
![]() $i=1,2$
. Since
$i=1,2$
. Since
![]() $\overline {M}_i$
is nef and non-degenerate, Yuan-Zhang’s fundamental inequality [Reference Yuan and ZhangYZ, Theorem 5.3.3] implies that
$\overline {M}_i$
is nef and non-degenerate, Yuan-Zhang’s fundamental inequality [Reference Yuan and ZhangYZ, Theorem 5.3.3] implies that
![]() $h_{\overline {M}_i}(\mathcal {X}_V^{\ell +1})=0$
for
$h_{\overline {M}_i}(\mathcal {X}_V^{\ell +1})=0$
for
![]() $i=1,2$
. We can use [Reference Yuan and ZhangYZ, Theorem 5.4.3] with the Galois-invariant critically small set to get that
$i=1,2$
. We can use [Reference Yuan and ZhangYZ, Theorem 5.4.3] with the Galois-invariant critically small set to get that
on
![]() $\mathcal {X}_V^{\ell +1}$
for some constant
$\mathcal {X}_V^{\ell +1}$
for some constant
![]() $\alpha>0$
.
$\alpha>0$
.
We now slice these measures with respect to the projection
![]() $\mathcal {X}_V^{\ell +1} \to \mathcal {X}_V^\ell $
; see, for example [Reference Bassanelli and BertelootBB, Proposition 4.3]. This implies that
$\mathcal {X}_V^{\ell +1} \to \mathcal {X}_V^\ell $
; see, for example [Reference Bassanelli and BertelootBB, Proposition 4.3]. This implies that
 $$ \begin{align} \int_{\mathcal{X}^{\ell}_V}\left( \int_{X_{\pi(x)}}\phi \cdot \bigwedge_{i=1}^r T_{f_{\ell+1},c_i}|_{X_{\pi(x)}}\right) d\mu_{\ell}(x) = \alpha \int_{\mathcal{X}^{\ell}_V}\left( \int_{X_{\pi(x)}}\phi \cdot \bigwedge_{i=2}^{r+1} T_{f_{\ell+1},c_i}|_{X_{\pi(x)}}\right) d\mu_{\ell}(x) \end{align} $$
$$ \begin{align} \int_{\mathcal{X}^{\ell}_V}\left( \int_{X_{\pi(x)}}\phi \cdot \bigwedge_{i=1}^r T_{f_{\ell+1},c_i}|_{X_{\pi(x)}}\right) d\mu_{\ell}(x) = \alpha \int_{\mathcal{X}^{\ell}_V}\left( \int_{X_{\pi(x)}}\phi \cdot \bigwedge_{i=2}^{r+1} T_{f_{\ell+1},c_i}|_{X_{\pi(x)}}\right) d\mu_{\ell}(x) \end{align} $$
for every continuous and compactly supported function
![]() $\phi $
on
$\phi $
on
![]() $\mathcal {X}^{\ell +1}_V$
. Here,
$\mathcal {X}^{\ell +1}_V$
. Here,
![]() $\pi : \mathcal {X}^{\ell }_V\to V$
denotes the projection to the base. (Strictly speaking, since the measure
$\pi : \mathcal {X}^{\ell }_V\to V$
denotes the projection to the base. (Strictly speaking, since the measure
![]() $\mu _\ell $
is not smooth, we should approximate
$\mu _\ell $
is not smooth, we should approximate
![]() $\mu _\ell $
by smooth and compactly-supported forms on
$\mu _\ell $
by smooth and compactly-supported forms on
![]() $\mathcal {X}_V^\ell $
to deduce (4.7); compare the proof of [Reference Myrto Mavraki and SchmidtMaS, Theorem 1.8].)
$\mathcal {X}_V^\ell $
to deduce (4.7); compare the proof of [Reference Myrto Mavraki and SchmidtMaS, Theorem 1.8].)
For each
![]() $\lambda \in V$
, set
$\lambda \in V$
, set
and
We infer from (4.7) that
as measures on
![]() $X_{\lambda }$
, for some constant
$X_{\lambda }$
, for some constant
![]() $\alpha>0$
and for all
$\alpha>0$
and for all
![]() $\lambda $
in the support of
$\lambda $
in the support of
![]() $\pi _*\mu _\ell $
in V. Indeed, suppose there exists
$\pi _*\mu _\ell $
in V. Indeed, suppose there exists
![]() $b \in V(\mathbb {C})$
where (4.8) doesn’t hold, and so that
$b \in V(\mathbb {C})$
where (4.8) doesn’t hold, and so that
![]() $\pi _{*}\mu _{\ell }(U)>0$
for every open neighborhood U of b. Then we can find a continuous, non-negative, compactly supported function
$\pi _{*}\mu _{\ell }(U)>0$
for every open neighborhood U of b. Then we can find a continuous, non-negative, compactly supported function
![]() $\psi $
on
$\psi $
on
![]() $\mathcal {X}$
such that
$\mathcal {X}$
such that
By weak continuity of the measures
![]() $\mu ^{r+1}_{\lambda }$
and
$\mu ^{r+1}_{\lambda }$
and
![]() $\mu _\lambda ^1$
as
$\mu _\lambda ^1$
as
![]() $\lambda $
varies (since the bifurcation currents have continuous potentials), we find that
$\lambda $
varies (since the bifurcation currents have continuous potentials), we find that
for all
![]() $\lambda $
in a small neighborhood U of b. Therefore, setting
$\lambda $
in a small neighborhood U of b. Therefore, setting
on
![]() $\mathcal {X}^{\ell +1}_V$
for a non-negative function
$\mathcal {X}^{\ell +1}_V$
for a non-negative function
![]() $h_b$
supported in a small neighborhood of b, the equality (4.7) will fail.
$h_b$
supported in a small neighborhood of b, the equality (4.7) will fail.
The remainder of the proof is devoted to deriving a contradiction from the equality (4.8). We first sketch the idea. Recall from Proposition 3.2 that we have parameter
![]() $x_1 = (\lambda _1, s_1, \ldots , s_\ell ) \in \operatorname {supp} \mu _\ell $
so that the tuple of marked critical points
$x_1 = (\lambda _1, s_1, \ldots , s_\ell ) \in \operatorname {supp} \mu _\ell $
so that the tuple of marked critical points
![]() $(c_1, \ldots , c_r)$
is transversely prerepelling for
$(c_1, \ldots , c_r)$
is transversely prerepelling for
![]() $F^{(\lambda _1)} = (f,\ldots , f)$
at
$F^{(\lambda _1)} = (f,\ldots , f)$
at
![]() $s_\ell $
over
$s_\ell $
over
![]() $X_{\lambda _1}$
. This implies that
$X_{\lambda _1}$
. This implies that
![]() $\mu _{\lambda _1}^{r+1}$
is nonzero on
$\mu _{\lambda _1}^{r+1}$
is nonzero on
![]() $X_{\lambda _1}$
, with
$X_{\lambda _1}$
, with
![]() $s_\ell $
in its support by [Reference Buff and EpsteinBE]. Moreover, as in [Reference Buff and EpsteinBE, Section 3] and the generalization appearing in [Reference GauthierGa2, Proposition 3.2], we know that if we zoom in on the measure
$s_\ell $
in its support by [Reference Buff and EpsteinBE]. Moreover, as in [Reference Buff and EpsteinBE, Section 3] and the generalization appearing in [Reference GauthierGa2, Proposition 3.2], we know that if we zoom in on the measure
![]() $\mu ^{r+1}_{\lambda _1}$
on
$\mu ^{r+1}_{\lambda _1}$
on
![]() $X_{\lambda _1}$
at the parameter
$X_{\lambda _1}$
at the parameter
![]() $s_\ell $
at an exponential rate in n (determined by the multipliers of the repelling cycles in the forward orbits of the marked critical points), and rescale the measure appropriately we get a nontrivial limit; see (4.11). On the other hand, we know from Proposition 3.2 that the critical point
$s_\ell $
at an exponential rate in n (determined by the multipliers of the repelling cycles in the forward orbits of the marked critical points), and rescale the measure appropriately we get a nontrivial limit; see (4.11). On the other hand, we know from Proposition 3.2 that the critical point
![]() $c_{r+1}$
is attracted to a parabolic cycle at
$c_{r+1}$
is attracted to a parabolic cycle at
![]() $s_{\ell }\in X_{\lambda _1}$
. Zooming into the measure
$s_{\ell }\in X_{\lambda _1}$
. Zooming into the measure
![]() $\mu _{\lambda _1}^1$
on
$\mu _{\lambda _1}^1$
on
![]() $X_{\lambda _1}$
at
$X_{\lambda _1}$
at
![]() $s_\ell $
at the same exponential rate (which is supposed to give a nonzero limit), we actually get 0 from the following lemma. This will produce our desired contradiction.
$s_\ell $
at the same exponential rate (which is supposed to give a nonzero limit), we actually get 0 from the following lemma. This will produce our desired contradiction.
Lemma 4.1. Suppose that
![]() $f: \mathbb {D}^r \times \mathbb {P}^1\to \mathbb {D}^r \times \mathbb {P}^1$
is a holomorphic family of maps with degree
$f: \mathbb {D}^r \times \mathbb {P}^1\to \mathbb {D}^r \times \mathbb {P}^1$
is a holomorphic family of maps with degree
![]() $d\ge 2$
parametrized by
$d\ge 2$
parametrized by
![]() $\mathbb {D}^r \subset \mathbb {C}^r$
with a marked critical point
$\mathbb {D}^r \subset \mathbb {C}^r$
with a marked critical point
![]() $c: \mathbb {D}^r \to \mathbb {P}^1$
. Assume that
$c: \mathbb {D}^r \to \mathbb {P}^1$
. Assume that
![]() $c(0)$
is attracted to a parabolic fixed point at
$c(0)$
is attracted to a parabolic fixed point at
![]() $z=0$
for
$z=0$
for
![]() $f_0$
. Then for any constant
$f_0$
. Then for any constant
![]() $\rho> 1$
, there exists
$\rho> 1$
, there exists
![]() $\delta>0$
so that the sequence of functions
$\delta>0$
so that the sequence of functions
converges uniformly to 0 on the polydisk
![]() $(\mathbb {D}_\delta )^r$
, as
$(\mathbb {D}_\delta )^r$
, as
![]() $n\to \infty $
.
$n\to \infty $
.
Proof. Let
![]() $\rho>1$
. Since
$\rho>1$
. Since
![]() $|f^{\prime }_0(0)| = 1$
, we can first fix a small
$|f^{\prime }_0(0)| = 1$
, we can first fix a small
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\rho _\varepsilon>1$
so that
$\rho _\varepsilon>1$
so that
for all
![]() $x\in \mathbb {D}^r_{\epsilon }$
and
$x\in \mathbb {D}^r_{\epsilon }$
and
![]() $z\in \mathbb {D}_\varepsilon $
. We replace c with an iterate so that
$z\in \mathbb {D}_\varepsilon $
. We replace c with an iterate so that
![]() $c(0)$
and all its forward iterates under
$c(0)$
and all its forward iterates under
![]() $f_0$
are in the disk
$f_0$
are in the disk
![]() $\mathbb {D}_{\varepsilon /2}$
. Choose
$\mathbb {D}_{\varepsilon /2}$
. Choose
![]() $M>0$
so that the gradient of f (with respect to parameter x) satisfies
$M>0$
so that the gradient of f (with respect to parameter x) satisfies
for all
![]() $x\in \mathbb {D}^r$
and
$x\in \mathbb {D}^r$
and
![]() $z\in \mathbb {D}_\varepsilon $
. Note that
$z\in \mathbb {D}_\varepsilon $
. Note that
Taking derivatives, we have
 $$ \begin{align} |\nabla \alpha_n(x)|&=\left|\frac{1}{\rho^n}\cdot (\nabla_w f_w) (\alpha_{n-1}(x/\rho))+\frac{1}{\rho} f_{x/\rho^n}'(\alpha_{n-1}(x/\rho)) \nabla_{x/\rho} \alpha_{n-1}(x/\rho) \right| \nonumber \\ &\leq \frac{M}{\rho^n} +\frac{\rho_\varepsilon}{\rho}\, |\nabla_{x/\rho}\alpha_{n-1}(x/\rho)| \end{align} $$
$$ \begin{align} |\nabla \alpha_n(x)|&=\left|\frac{1}{\rho^n}\cdot (\nabla_w f_w) (\alpha_{n-1}(x/\rho))+\frac{1}{\rho} f_{x/\rho^n}'(\alpha_{n-1}(x/\rho)) \nabla_{x/\rho} \alpha_{n-1}(x/\rho) \right| \nonumber \\ &\leq \frac{M}{\rho^n} +\frac{\rho_\varepsilon}{\rho}\, |\nabla_{x/\rho}\alpha_{n-1}(x/\rho)| \end{align} $$
as long as
![]() $\alpha _{n-1}(x/\rho )$
lies in
$\alpha _{n-1}(x/\rho )$
lies in
![]() $\mathbb {D}_\varepsilon $
.
$\mathbb {D}_\varepsilon $
.
Now choose
![]() $n_0$
so that
$n_0$
so that
We take a very small
![]() $\delta _1$
so that
$\delta _1$
so that
for all
![]() $x \in \mathbb {D}_{\delta _1}^r$
, and set
$x \in \mathbb {D}_{\delta _1}^r$
, and set
From the inequality (4.9), we have
for each
![]() $x\in \mathbb {D}_{\delta _1}^r$
. Let
$x\in \mathbb {D}_{\delta _1}^r$
. Let
and define
![]() $M_i$
recursively by
$M_i$
recursively by
for
![]() $i\geq 2$
. Note that
$i\geq 2$
. Note that
![]() $M_i \to 0$
as
$M_i \to 0$
as
![]() $i\to \infty $
, because
$i\to \infty $
, because
 $$ \begin{align*}M_i = \left(\frac{\rho_\varepsilon}{\rho}\right)^{i-1}(M_1+1) + \frac{1}{\rho^i} \sum_{j=1}^{i-2} \rho_\varepsilon^j.\end{align*} $$
$$ \begin{align*}M_i = \left(\frac{\rho_\varepsilon}{\rho}\right)^{i-1}(M_1+1) + \frac{1}{\rho^i} \sum_{j=1}^{i-2} \rho_\varepsilon^j.\end{align*} $$
Finally, we can show inductively that our derivative estimate (4.9) holds when applied to
![]() $\alpha _n$
for all
$\alpha _n$
for all
![]() $n> n_0$
on a sufficiently small disk near 0. This will imply that
$n> n_0$
on a sufficiently small disk near 0. This will imply that
for all x in a small disk around 0. We know it holds for
![]() $i=0$
for all
$i=0$
for all
![]() $|x| < \delta _1$
. We take
$|x| < \delta _1$
. We take
![]() $M_0:=\max _{i\geq 2} M_i$
, and set
$M_0:=\max _{i\geq 2} M_i$
, and set
As
![]() $\alpha _{n_0}(0)\in \mathbb {D}_{\varepsilon /2}$
, the inequality (4.9) gives
$\alpha _{n_0}(0)\in \mathbb {D}_{\varepsilon /2}$
, the inequality (4.9) gives
![]() $|\nabla \alpha _{n_0}(x)|<M_2\leq M_0$
, so that
$|\nabla \alpha _{n_0}(x)|<M_2\leq M_0$
, so that
![]() $\alpha _{n_0}(x)$
is in
$\alpha _{n_0}(x)$
is in
![]() $\mathbb {D}_{\varepsilon }$
for each
$\mathbb {D}_{\varepsilon }$
for each
![]() $x\in \mathbb {D}^r_{\delta }$
. By induction, we see that if
$x\in \mathbb {D}^r_{\delta }$
. By induction, we see that if
![]() $\alpha _{n_0+i-1}(x)$
is in
$\alpha _{n_0+i-1}(x)$
is in
![]() $\mathbb {D}_{\varepsilon }$
with
$\mathbb {D}_{\varepsilon }$
with
![]() $|\nabla \alpha _{n_0+i-1}|\leq M_{i+1}$
, then
$|\nabla \alpha _{n_0+i-1}|\leq M_{i+1}$
, then
![]() $\alpha _{n_0+i}(x)$
is in
$\alpha _{n_0+i}(x)$
is in
![]() $\mathbb {D}_{\varepsilon }$
, because
$\mathbb {D}_{\varepsilon }$
, because
![]() $\alpha _{n_0+i}(0)$
is in
$\alpha _{n_0+i}(0)$
is in
![]() $\mathbb {D}_{\varepsilon /2}$
and
$\mathbb {D}_{\varepsilon /2}$
and
![]() $\delta <\varepsilon /(2M_0)$
. Since
$\delta <\varepsilon /(2M_0)$
. Since
![]() $M_i\to 0$
as i tends to infinity, we see that
$M_i\to 0$
as i tends to infinity, we see that
![]() $\alpha _n$
converges to
$\alpha _n$
converges to
![]() $0$
uniformly on
$0$
uniformly on
![]() $\mathbb {D}^r_\delta $
.
$\mathbb {D}^r_\delta $
.
We now return to our proof. Abusing the notation slightly, we write
![]() $\{f_s\}_{s\in X_{\lambda _1}}$
to denote the restriction of the family of maps to
$\{f_s\}_{s\in X_{\lambda _1}}$
to denote the restriction of the family of maps to
![]() $X_{\lambda _1}$
,
$X_{\lambda _1}$
,
![]() $c_{r+1}$
for the restriction of
$c_{r+1}$
for the restriction of
![]() $c_{r+1}$
to
$c_{r+1}$
to
![]() $X_{\lambda _1}$
, and
$X_{\lambda _1}$
, and
![]() $T_{c_{r+1}}$
its associated bifurcation current on
$T_{c_{r+1}}$
its associated bifurcation current on
![]() $X_{\lambda _1}$
. We know from Lemma 4.1 that, zooming into
$X_{\lambda _1}$
. We know from Lemma 4.1 that, zooming into
![]() $s_\ell $
in
$s_\ell $
in
![]() $X_{\lambda _1}$
at any exponential rate, the graphs of iterates of
$X_{\lambda _1}$
at any exponential rate, the graphs of iterates of
![]() $c_{r+1}$
are converging to the graph of a constant function.
$c_{r+1}$
are converging to the graph of a constant function.
Let
![]() $p_0\in \mathbb {P}^1$
be the parabolic periodic point of
$p_0\in \mathbb {P}^1$
be the parabolic periodic point of
![]() $f_{s_\ell }$
; replacing
$f_{s_\ell }$
; replacing
![]() $f_{s_\ell }$
with an iterate, we have
$f_{s_\ell }$
with an iterate, we have
![]() $f_{s_\ell }^n(c_{r+1}(s_\ell ))\to p_0$
as
$f_{s_\ell }^n(c_{r+1}(s_\ell ))\to p_0$
as
![]() $n\to \infty $
. After a change of coordinates if necessary, we may assume that
$n\to \infty $
. After a change of coordinates if necessary, we may assume that
![]() $c_{r+1}(s_\ell )$
and
$c_{r+1}(s_\ell )$
and
![]() $p_0$
are not
$p_0$
are not
![]() $\infty $
. Recalling the definition of the bifurcation current associated to
$\infty $
. Recalling the definition of the bifurcation current associated to
![]() $c_{r+1}$
, we can work in homogeneous coordinates on
$c_{r+1}$
, we can work in homogeneous coordinates on
![]() $\mathbb {P}^1$
over a neighborhood of
$\mathbb {P}^1$
over a neighborhood of
![]() $s_\ell $
in
$s_\ell $
in
![]() $X_{\lambda _1}$
. We define
$X_{\lambda _1}$
. We define
with a choice of homogeneous lift
![]() $F_{s}$
for
$F_{s}$
for
![]() $f_{s}$
normalized so that
$f_{s}$
normalized so that
![]() $G_{s_\ell }(p_0,1)= 0$
. Note that
$G_{s_\ell }(p_0,1)= 0$
. Note that
![]() $G_s(c_{r+1}(s), 1)$
is a potential of the bifurcation current
$G_s(c_{r+1}(s), 1)$
is a potential of the bifurcation current
![]() $T_{c_{r+1}}$
on a neighborhood of
$T_{c_{r+1}}$
on a neighborhood of
![]() $s_\ell \in X_{\lambda _1}$
. As long as
$s_\ell \in X_{\lambda _1}$
. As long as
![]() $f^n_s(c_{r+1}(s))$
is not
$f^n_s(c_{r+1}(s))$
is not
![]() $\infty $
, which is always true when s is in
$\infty $
, which is always true when s is in
![]() $ \mathbb {D}(s_\ell , \delta /\rho ^n)$
for small
$ \mathbb {D}(s_\ell , \delta /\rho ^n)$
for small
![]() $\delta>0$
, any
$\delta>0$
, any
![]() $\rho>1$
and big n by Lemma 4.1, we define
$\rho>1$
and big n by Lemma 4.1, we define
so that
where defined, as
![]() $G_s(F^n_s(c_{r+1}(s),1)) = d^n\cdot G_s(c_{r+1}(s),1)$
differs from
$G_s(F^n_s(c_{r+1}(s),1)) = d^n\cdot G_s(c_{r+1}(s),1)$
differs from
![]() $U_n(s)$
by a harmonic function.
$U_n(s)$
by a harmonic function.
Let
![]() $r_0$
be any biholomorphic map from
$r_0$
be any biholomorphic map from
![]() $\mathbb {D}^{r}$
to a neighborhood of
$\mathbb {D}^{r}$
to a neighborhood of
![]() $s_\ell \in X_{\lambda _1}$
, with
$s_\ell \in X_{\lambda _1}$
, with
![]() $r_0(0)=s_\ell $
. From Lemma 4.1 and the choice of our lift, we deduce that, for any
$r_0(0)=s_\ell $
. From Lemma 4.1 and the choice of our lift, we deduce that, for any
![]() $\rho>1$
, the functions
$\rho>1$
, the functions
![]() $U_n\circ r_0(y/\rho ^n)$
converge uniformly to
$U_n\circ r_0(y/\rho ^n)$
converge uniformly to
![]() $G_{s_{\ell }}(p_0,1)=0$
on a small neighborhood of
$G_{s_{\ell }}(p_0,1)=0$
on a small neighborhood of
![]() $(0, \ldots , 0)\in \mathbb {D}^{r}$
. As a consequence, for any
$(0, \ldots , 0)\in \mathbb {D}^{r}$
. As a consequence, for any
![]() $\rho _i\in \mathbb {C}$
with
$\rho _i\in \mathbb {C}$
with
![]() $|\rho _i|>1$
, we can pick some
$|\rho _i|>1$
, we can pick some
![]() $\rho>1$
with
$\rho>1$
with
![]() $\rho < \min _{1\leq i\leq {r}} (|\rho _i|)$
so that the sequence of functions
$\rho < \min _{1\leq i\leq {r}} (|\rho _i|)$
so that the sequence of functions
uniformly, as
![]() $A_n(y):=(y_1\cdot \rho ^n/\rho _1^n, \ldots , y_{r}\cdot \rho ^n/\rho _{r}^n)$
converges to zero uniformly for
$A_n(y):=(y_1\cdot \rho ^n/\rho _1^n, \ldots , y_{r}\cdot \rho ^n/\rho _{r}^n)$
converges to zero uniformly for
![]() $n\to \infty $
.
$n\to \infty $
.
Following the notation of [Reference GauthierGa2, Proposition 3.2], we now let
![]() $r_n: \mathbb {D}^r \to X_{\lambda _1}$
be the sequence of maps that define the zooms near the parameter
$r_n: \mathbb {D}^r \to X_{\lambda _1}$
be the sequence of maps that define the zooms near the parameter
![]() $s_\ell $
for the measure
$s_\ell $
for the measure
![]() $\mu ^{r+1}_{\lambda _1}$
corresponding to the transversely prerepelling critical point at
$\mu ^{r+1}_{\lambda _1}$
corresponding to the transversely prerepelling critical point at
![]() $x_1$
, as described before Lemma 4.1. From [Reference GauthierGa2, Proposition 3.2] we know that there is a measure
$x_1$
, as described before Lemma 4.1. From [Reference GauthierGa2, Proposition 3.2] we know that there is a measure
![]() $\mu \neq 0$
(which can be described explicitly) such that
$\mu \neq 0$
(which can be described explicitly) such that
uniformly as
![]() $n\to \infty $
. On the other hand, it follows from (4.10) that the functions
$n\to \infty $
. On the other hand, it follows from (4.10) that the functions
![]() $U_n\circ r_n$
also converge uniformly to 0. We conclude that
$U_n\circ r_n$
also converge uniformly to 0. We conclude that
![]() $d^n \, (r_n)^{*} T_{c_{r+1}} \to 0$
weakly, and therefore
$d^n \, (r_n)^{*} T_{c_{r+1}} \to 0$
weakly, and therefore
Therefore,
![]() $\mu ^1_{\lambda _1}$
cannot be proportional to
$\mu ^1_{\lambda _1}$
cannot be proportional to
![]() $\mu ^{r+1}_{\lambda _1}$
, contradicting (4.8). This completes the proof of Theorem 1.8.
$\mu ^{r+1}_{\lambda _1}$
, contradicting (4.8). This completes the proof of Theorem 1.8.
Remark 4.2. The proof would simplify if we knew that the
![]() $(r+1)$
-th critical point
$(r+1)$
-th critical point
![]() $c_{r+1}$
were preperiodic to a parabolic cycle, instead of only in the basin of that cycle. We could employ ideas that appeared in [Reference Ghioca, Nguyen and YeGNY, Proposition 5.2] (written for measures in the dynamical plane) or the proof of [Reference Favre and GauthierFG3, Proposition 5.12] (for
$c_{r+1}$
were preperiodic to a parabolic cycle, instead of only in the basin of that cycle. We could employ ideas that appeared in [Reference Ghioca, Nguyen and YeGNY, Proposition 5.2] (written for measures in the dynamical plane) or the proof of [Reference Favre and GauthierFG3, Proposition 5.12] (for
![]() $1$
-parameter families of polynomials and marked points). But the critical point
$1$
-parameter families of polynomials and marked points). But the critical point
![]() $c_{r+1}$
is sometimes the only “free” critical point and must therefore have an infinite orbit in the presence of a parabolic cycle.
$c_{r+1}$
is sometimes the only “free” critical point and must therefore have an infinite orbit in the presence of a parabolic cycle.
5 Proofs of Theorems 1.1, 1.2, 1.5, and 1.6
An elementary, but important, geometric observation is the following [Reference Gao, Ge and KühneGGK, Lemma 4.3]: If
![]() $\Sigma $
is a subset of a complex projective algebraic variety X, equipped with an ample line bundle L, and if the product
$\Sigma $
is a subset of a complex projective algebraic variety X, equipped with an ample line bundle L, and if the product
![]() $\Sigma ^M$
lies in a proper subvariety
$\Sigma ^M$
lies in a proper subvariety
![]() $Y \subset X^M$
for some integer
$Y \subset X^M$
for some integer
![]() $M\geq 1$
, then
$M\geq 1$
, then
![]() $\Sigma $
must be contained in a proper subvariety Z of X, where the number of components of Z and the degree of each are bounded by constants depending only on M,
$\Sigma $
must be contained in a proper subvariety Z of X, where the number of components of Z and the degree of each are bounded by constants depending only on M,
![]() $\dim X$
, the degree of X, and the sum of the degrees of the components of Y. Here, we measure degree in
$\dim X$
, the degree of X, and the sum of the degrees of the components of Y. Here, we measure degree in
![]() $X^M$
with respect to the ample line bundle
$X^M$
with respect to the ample line bundle
![]() $p_1^*L \otimes \cdots \otimes p_M^*L$
on
$p_1^*L \otimes \cdots \otimes p_M^*L$
on
![]() $X^M$
, where
$X^M$
, where
![]() $p_i: X^M \to X$
is the projection to the i-th factor.
$p_i: X^M \to X$
is the projection to the i-th factor.
Fix degree
![]() $d\geq 2$
. For positive integers r and D, we will apply Theorem 1.8 to families
$d\geq 2$
. For positive integers r and D, we will apply Theorem 1.8 to families
![]() $\mathcal {X} \to V$
over a subvariety
$\mathcal {X} \to V$
over a subvariety
![]() $V \subset \mathrm {Ch}(\mathrm {M}_d, r,D)$
, all defined over
$V \subset \mathrm {Ch}(\mathrm {M}_d, r,D)$
, all defined over
![]() $\overline {\mathbb {Q}}$
. We work inductively on the dimension r of the fibers in the family.
$\overline {\mathbb {Q}}$
. We work inductively on the dimension r of the fibers in the family.
First suppose that
![]() $\mathcal {C} \to V$
is a family of curves in
$\mathcal {C} \to V$
is a family of curves in
![]() $\mathrm {M}_d$
of degree
$\mathrm {M}_d$
of degree
![]() $\leq D$
, with irreducible
$\leq D$
, with irreducible
![]() $V \subset \mathrm {Ch}(\mathrm {M}_d, 1, D)$
defined over
$V \subset \mathrm {Ch}(\mathrm {M}_d, 1, D)$
defined over
![]() $\overline {\mathbb {Q}}$
and of dimension
$\overline {\mathbb {Q}}$
and of dimension
![]() $\ell \geq 1$
, and assume that the generic fiber of
$\ell \geq 1$
, and assume that the generic fiber of
![]() $\mathcal {C} \to V$
is geometrically irreducible. From Theorem 1.8 applied to the fiber power
$\mathcal {C} \to V$
is geometrically irreducible. From Theorem 1.8 applied to the fiber power
![]() $\mathcal {C}_V^{\ell +1}$
, we know that there exists an
$\mathcal {C}_V^{\ell +1}$
, we know that there exists an
![]() $\varepsilon = \varepsilon (\mathcal {C})$
so that points
$\varepsilon = \varepsilon (\mathcal {C})$
so that points
![]() $(\lambda , f_1, \ldots , f_{\ell +1}) \in \mathcal {C}_V^{\ell +1}(\overline {\mathbb {Q}})$
with
$(\lambda , f_1, \ldots , f_{\ell +1}) \in \mathcal {C}_V^{\ell +1}(\overline {\mathbb {Q}})$
with
![]() $\sum _i \hat {h}_{\mathrm {crit}}(f_i) < \varepsilon \max \{1,h_{\mathrm {Ch}}(\lambda )\}$
are not Zariski dense. We let
$\sum _i \hat {h}_{\mathrm {crit}}(f_i) < \varepsilon \max \{1,h_{\mathrm {Ch}}(\lambda )\}$
are not Zariski dense. We let
![]() $Z_\varepsilon $
denote the Zariski closure of this set in
$Z_\varepsilon $
denote the Zariski closure of this set in
![]() $\mathcal {C}_V^{\ell +1}$
, over
$\mathcal {C}_V^{\ell +1}$
, over
![]() $\overline {\mathbb {Q}}$
. It follows that there is a Zariski open
$\overline {\mathbb {Q}}$
. It follows that there is a Zariski open
![]() $U \subset V$
(defined over
$U \subset V$
(defined over
![]() $\overline {\mathbb {Q}}$
) so that
$\overline {\mathbb {Q}}$
) so that
![]() $Z_\varepsilon \cap C_\lambda ^{\ell +1}$
is a proper algebraic subvariety of
$Z_\varepsilon \cap C_\lambda ^{\ell +1}$
is a proper algebraic subvariety of
![]() $(C_\lambda )^{\ell +1}$
for all
$(C_\lambda )^{\ell +1}$
for all
![]() $\lambda \in U(\mathbb {C})$
, with its number of irreducible components bounded over
$\lambda \in U(\mathbb {C})$
, with its number of irreducible components bounded over
![]() $\lambda \in U(\mathbb {C})$
. It is worth noting that all points
$\lambda \in U(\mathbb {C})$
. It is worth noting that all points
![]() $(\lambda , f_1, \ldots , f_{\ell +1}) \in \mathcal {C}_V^{\ell +1}(\mathbb {C})$
where each
$(\lambda , f_1, \ldots , f_{\ell +1}) \in \mathcal {C}_V^{\ell +1}(\mathbb {C})$
where each
![]() $f_i$
is in
$f_i$
is in
![]() $\mathrm {M}_d(\overline {\mathbb {Q}})$
with
$\mathrm {M}_d(\overline {\mathbb {Q}})$
with
![]() $\sum _i \hat {h}_{\mathrm {crit}}(f_i) < \varepsilon $
must lie in
$\sum _i \hat {h}_{\mathrm {crit}}(f_i) < \varepsilon $
must lie in
![]() $Z_\varepsilon $
, also for
$Z_\varepsilon $
, also for
![]() $\lambda \in V(\mathbb {C}) \setminus V(\overline {\mathbb {Q}})$
; indeed, any such
$\lambda \in V(\mathbb {C}) \setminus V(\overline {\mathbb {Q}})$
; indeed, any such
![]() $(\ell +1)$
-tuple must lie in a family of curves in V defined over
$(\ell +1)$
-tuple must lie in a family of curves in V defined over
![]() $\overline {\mathbb {Q}}$
that includes this
$\overline {\mathbb {Q}}$
that includes this
![]() $C_\lambda $
.
$C_\lambda $
.
We now apply [Reference Gao, Ge and KühneGGK, Lemma 4.3] to the set
for
![]() $\lambda \in U(\overline {\mathbb {Q}})$
, and to
$\lambda \in U(\overline {\mathbb {Q}})$
, and to
for
![]() $\lambda \in U(\mathbb {C})\setminus U(\overline {\mathbb {Q}})$
, so that
$\lambda \in U(\mathbb {C})\setminus U(\overline {\mathbb {Q}})$
, so that
![]() $\Sigma _{\lambda ,\varepsilon }^{\ell +1}\subset Z_{\varepsilon }\cap C^{\ell +1}_{\lambda }$
for all
$\Sigma _{\lambda ,\varepsilon }^{\ell +1}\subset Z_{\varepsilon }\cap C^{\ell +1}_{\lambda }$
for all
![]() $\lambda \in U(\mathbb {C})$
. We deduce the existence of a constant N so that
$\lambda \in U(\mathbb {C})$
. We deduce the existence of a constant N so that
![]() $|\Sigma _{\lambda ,\varepsilon }| \leq N$
for all
$|\Sigma _{\lambda ,\varepsilon }| \leq N$
for all
![]() $\lambda \in U(\mathbb {C})$
. Note here that we have used the fact that the number of components of
$\lambda \in U(\mathbb {C})$
. Note here that we have used the fact that the number of components of
![]() $Z_{\varepsilon }\cap C^{\ell +1}_{\lambda }$
and the degree of each is uniformly bounded for
$Z_{\varepsilon }\cap C^{\ell +1}_{\lambda }$
and the degree of each is uniformly bounded for
![]() $\lambda \in U(\mathbb {C})$
(controlled by the geometry of its generic fiber). Note also that if
$\lambda \in U(\mathbb {C})$
(controlled by the geometry of its generic fiber). Note also that if
![]() $0\le \varepsilon '<\varepsilon $
, then
$0\le \varepsilon '<\varepsilon $
, then
![]() $\Sigma _{\lambda ,\varepsilon '}\subset \Sigma _{\lambda ,\varepsilon }$
and hence
$\Sigma _{\lambda ,\varepsilon '}\subset \Sigma _{\lambda ,\varepsilon }$
and hence
![]() $|\Sigma _{\lambda ,\varepsilon '}|\leq N$
for each
$|\Sigma _{\lambda ,\varepsilon '}|\leq N$
for each
![]() $\lambda \in U(\mathbb {C})$
.
$\lambda \in U(\mathbb {C})$
.
We then repeat the argument with the families of curves over the positive-dimensional components in the complement of
![]() $V\setminus U$
; we work with irreducible components so that the generic fibers of these families will be (geometrically) irreducible. Note that each family we treat is defined over
$V\setminus U$
; we work with irreducible components so that the generic fibers of these families will be (geometrically) irreducible. Note that each family we treat is defined over
![]() $\overline {\mathbb {Q}}$
. We increase the bound N and decrease
$\overline {\mathbb {Q}}$
. We increase the bound N and decrease
![]() $\epsilon $
as needed. We are left with a finite set S in
$\epsilon $
as needed. We are left with a finite set S in
![]() $V(\overline {\mathbb {Q}})$
containing all of the irreducible PCF-special curves with degree
$V(\overline {\mathbb {Q}})$
containing all of the irreducible PCF-special curves with degree
![]() $\leq D$
as well as all curves in V with infinitely many points of critical height
$\leq D$
as well as all curves in V with infinitely many points of critical height
![]() $< \frac {\varepsilon }{\ell +1}\max \{1,h_{\mathrm {Ch}}(\lambda )\}$
(or
$< \frac {\varepsilon }{\ell +1}\max \{1,h_{\mathrm {Ch}}(\lambda )\}$
(or
![]() $< \frac {\varepsilon }{\ell +1}$
over complex parameters). This proves Theorems 1.2 and 1.6 for the curves in V. If for any of the curves
$< \frac {\varepsilon }{\ell +1}$
over complex parameters). This proves Theorems 1.2 and 1.6 for the curves in V. If for any of the curves
![]() $C_\lambda $
in this leftover finite set
$C_\lambda $
in this leftover finite set
![]() $S \subset V(\overline {\mathbb {Q}})$
, we have
$S \subset V(\overline {\mathbb {Q}})$
, we have
![]() $N<|\Sigma _{\lambda ,\varepsilon }|<\infty $
, we just increase the bound N as needed so that Theorem 1.5 and 1.2 hold for all curves in V. We repeat the argument for all irreducible components V of
$N<|\Sigma _{\lambda ,\varepsilon }|<\infty $
, we just increase the bound N as needed so that Theorem 1.5 and 1.2 hold for all curves in V. We repeat the argument for all irreducible components V of
![]() $\mathrm {Ch}(\mathrm {M}_d, 1, D)$
with geometrically irreducible generic fiber and adjust the constants
$\mathrm {Ch}(\mathrm {M}_d, 1, D)$
with geometrically irreducible generic fiber and adjust the constants
![]() $\varepsilon ,~N$
as needed. This proves Theorems 1.1, 1.2, 1.5 and 1.6 for curves.
$\varepsilon ,~N$
as needed. This proves Theorems 1.1, 1.2, 1.5 and 1.6 for curves.
Now fix
![]() $r>1$
and suppose we know the conclusion of Theorems 1.1, 1.2, 1.5, and 1.6 for subvarieties in
$r>1$
and suppose we know the conclusion of Theorems 1.1, 1.2, 1.5, and 1.6 for subvarieties in
![]() $\mathrm {M}_d$
of dimension
$\mathrm {M}_d$
of dimension
![]() $<r$
. Consider any family
$<r$
. Consider any family
![]() $\mathcal {X} \to V$
of r-dimensional varieties in
$\mathcal {X} \to V$
of r-dimensional varieties in
![]() $\mathrm {M}_d$
over an irreducible and quasiprojective
$\mathrm {M}_d$
over an irreducible and quasiprojective
![]() $V \subset \mathrm {Ch}(\mathrm {M}_d, r, D)$
defined over
$V \subset \mathrm {Ch}(\mathrm {M}_d, r, D)$
defined over
![]() $\overline {\mathbb {Q}}$
and of dimension
$\overline {\mathbb {Q}}$
and of dimension
![]() $\ell \geq 1$
for which the generic fiber of
$\ell \geq 1$
for which the generic fiber of
![]() $\mathcal {X} \to V$
is geometrically irreducible.
$\mathcal {X} \to V$
is geometrically irreducible.
As in the case of curves, we infer from Theorem 1.8 that there exists
![]() $\varepsilon = \varepsilon (\mathcal {X})>0$
so that all points
$\varepsilon = \varepsilon (\mathcal {X})>0$
so that all points
![]() $(\lambda , f_1, \ldots , f_{\ell +1}) \in \mathcal {X}_V^{\ell +1}(\overline {\mathbb {Q}})$
where each
$(\lambda , f_1, \ldots , f_{\ell +1}) \in \mathcal {X}_V^{\ell +1}(\overline {\mathbb {Q}})$
where each
![]() $f_i$
is in
$f_i$
is in
![]() $\mathrm {M}_d(\overline {\mathbb {Q}})$
with
$\mathrm {M}_d(\overline {\mathbb {Q}})$
with
![]() $\sum _i \hat {h}_{\mathrm {crit}}(f_i) < \varepsilon \max \{1,h_{\mathrm {Ch}}(\lambda )\}$
lie in a proper closed subvariety
$\sum _i \hat {h}_{\mathrm {crit}}(f_i) < \varepsilon \max \{1,h_{\mathrm {Ch}}(\lambda )\}$
lie in a proper closed subvariety
![]() $Z_\varepsilon $
in
$Z_\varepsilon $
in
![]() $\mathcal {X}_V^{\ell +1}$
. Therefore, as before, from [Reference Gao, Ge and KühneGGK, Lemma 4.3], there is a Zariski-open subset
$\mathcal {X}_V^{\ell +1}$
. Therefore, as before, from [Reference Gao, Ge and KühneGGK, Lemma 4.3], there is a Zariski-open subset
![]() $U\subset V$
(defined over
$U\subset V$
(defined over
![]() $\overline {\mathbb {Q}}$
) and constants
$\overline {\mathbb {Q}}$
) and constants
![]() $N_1$
and
$N_1$
and
![]() $B_1$
so that the points of
$B_1$
so that the points of
for
![]() $\lambda \in U(\overline {\mathbb {Q}})$
, and of
$\lambda \in U(\overline {\mathbb {Q}})$
, and of
for
![]() $\lambda \in U(\mathbb {C})\setminus U(\overline {\mathbb {Q}})$
, lie in a proper algebraic subvariety
$\lambda \in U(\mathbb {C})\setminus U(\overline {\mathbb {Q}})$
, lie in a proper algebraic subvariety
![]() $Z_{(\lambda )} \subset X_\lambda $
which has
$Z_{(\lambda )} \subset X_\lambda $
which has
![]() $\leq N_1$
irreducible components, each with degree
$\leq N_1$
irreducible components, each with degree
![]() $\leq B_1$
, for all
$\leq B_1$
, for all
![]() $\lambda \in U(\mathbb {C})$
. Note that
$\lambda \in U(\mathbb {C})$
. Note that
![]() $\Sigma ^r_{\lambda ,\epsilon }$
is not necessarily Zariski dense in
$\Sigma ^r_{\lambda ,\epsilon }$
is not necessarily Zariski dense in
![]() $Z_{(\lambda )}$
, so we apply the induction hypotheses (specifically, the constants from each of the statements of Theorems 1.1, 1.2, 1.5, 1.6 for subvarieties of dimension
$Z_{(\lambda )}$
, so we apply the induction hypotheses (specifically, the constants from each of the statements of Theorems 1.1, 1.2, 1.5, 1.6 for subvarieties of dimension
![]() $< r$
) to each irreducible component
$< r$
) to each irreducible component
![]() $Y_{(\lambda )}$
of
$Y_{(\lambda )}$
of
![]() $Z_{(\lambda )}$
, for all
$Z_{(\lambda )}$
, for all
![]() $\lambda \in U(\mathbb {C})$
. Thus, by reducing
$\lambda \in U(\mathbb {C})$
. Thus, by reducing
![]() $\varepsilon $
if needed, we conclude that the Zariski-closure of
$\varepsilon $
if needed, we conclude that the Zariski-closure of
![]() $\Sigma ^r_{\lambda ,\varepsilon }\cap Y_{(\lambda )}$
has uniformly bounded number of components, each with uniformly bounded degree for all
$\Sigma ^r_{\lambda ,\varepsilon }\cap Y_{(\lambda )}$
has uniformly bounded number of components, each with uniformly bounded degree for all
![]() $\lambda \in U(\mathbb {C})$
. Further, adjusting these uniform bounds if needed, using the induction hypothesis, we can arrange that they also bound the geometry of the Zariski closure of
$\lambda \in U(\mathbb {C})$
. Further, adjusting these uniform bounds if needed, using the induction hypothesis, we can arrange that they also bound the geometry of the Zariski closure of
![]() $\Sigma ^r_{\lambda , \varepsilon '}\cap Y_{(\lambda )}\subset \Sigma ^r_{\lambda , \varepsilon }\cap Y_{(\lambda )}$
for all
$\Sigma ^r_{\lambda , \varepsilon '}\cap Y_{(\lambda )}\subset \Sigma ^r_{\lambda , \varepsilon }\cap Y_{(\lambda )}$
for all
![]() $0\le \varepsilon '<\varepsilon $
(and in particular of
$0\le \varepsilon '<\varepsilon $
(and in particular of
![]() $Y_{(\lambda )} \cap \mathrm {PCF}_d$
). Combined with the initial bound of
$Y_{(\lambda )} \cap \mathrm {PCF}_d$
). Combined with the initial bound of
![]() $N_1$
on the number of components of
$N_1$
on the number of components of
![]() $Z_{(\lambda )}$
, repeating this procedure provides uniform bounds on the Zariski closures of
$Z_{(\lambda )}$
, repeating this procedure provides uniform bounds on the Zariski closures of
![]() $\Sigma ^r_{\lambda ,\varepsilon '}$
for all
$\Sigma ^r_{\lambda ,\varepsilon '}$
for all
![]() $\varepsilon '<\varepsilon $
and of
$\varepsilon '<\varepsilon $
and of
![]() $\overline {X_\lambda \cap \mathrm {PCF}_d}$
for all
$\overline {X_\lambda \cap \mathrm {PCF}_d}$
for all
![]() $\lambda \in U(\mathbb {C})$
.
$\lambda \in U(\mathbb {C})$
.
We now repeat the argument over each of the irreducible components of the complement
![]() $V \setminus U$
corresponding to families with geometrically irreducible generic fibers, and we note that each family we treat is defined over
$V \setminus U$
corresponding to families with geometrically irreducible generic fibers, and we note that each family we treat is defined over
![]() $\overline {\mathbb {Q}}$
. Finally, we are left with a finite set S in
$\overline {\mathbb {Q}}$
. Finally, we are left with a finite set S in
![]() $V(\overline {\mathbb {Q}})$
consisting of r-dimensional varieties that are either PCF-special or contain a Zariski-dense set of points in
$V(\overline {\mathbb {Q}})$
consisting of r-dimensional varieties that are either PCF-special or contain a Zariski-dense set of points in
![]() $\Sigma ^r_{\lambda , \varepsilon }$
. We repeat the arguments above for curves, reducing
$\Sigma ^r_{\lambda , \varepsilon }$
. We repeat the arguments above for curves, reducing
![]() $\varepsilon $
and increasing B and N as needed, once again appealing to the induction hypotheses. We have thus completed the proofs of Theorems 1.1, 1.2, 1.5, and 1.6.
$\varepsilon $
and increasing B and N as needed, once again appealing to the induction hypotheses. We have thus completed the proofs of Theorems 1.1, 1.2, 1.5, and 1.6.
Acknowledgments
We would like to thank Dori Bejleri, Xavier Buff, Ziyang Gao, Thomas Gauthier, Zhuchao Ji, Lars Kühne, Harry Schmidt, Gabriel Vigny, and Junyi Xie for helpful discussions. We also thank the anonymous referees for their comments and suggestions. In addition, we acknowledge the Radcliffe Institute for Advanced Study at Harvard, the University of Toronto, and the Fields Institute.
Competing interest
The author has no competing interest to declare.
Financial support
Our research was supported in part by the National Science Foundation, by the Natural Sciences and Engineering Research Council of Canada, by National Key R&D Program of China (
![]() $2021$
YFA
$2021$
YFA
![]() $1003202$
), and by NSFC (
$1003202$
), and by NSFC (
![]() $12131016$
,
$12131016$
,
![]() $12331004$
).
$12331004$
).