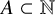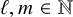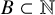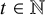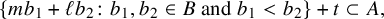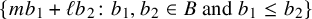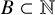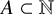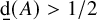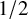1 Introduction
In [Reference Kra, Moreira, Richter and Robertson15], Kra, Moreira, Richter and Robertson established – among other things – the following result, resolving a well-known conjecture of Erdős.
Theorem 1.1 [Reference Kra, Moreira, Richter and Robertson15, Theorem 1.2].
For any
$A\subset {\mathbb N}$
with positive upper Banach density there exists some infinite set
$B\subset {\mathbb N}$
and a number
$t\in {\mathbb N}$
such that
$$ \begin{align*}\{b_1 + b_2\colon b_1,b_2\in B,\ b_1 \neq b_2\} + t \subset A.\end{align*} $$
For completeness, we recall that for a set
$A\subset {\mathbb N}$
its upper Banach density, denoted by
$\mathop {}\!\mathrm {d}^{*}(A)$
, is defined as the limit
$$ \begin{align*}\mathop{}\!\mathrm{d}^{*}(A)=\limsup_{N-M \to \infty} \frac{|A\cap \{M,M+1,\dots,N-1\}|}{N-M}.\end{align*} $$
More recently, the same set of authors proposed a conjecture (see [Reference Kra, Moreira, Richter and Robertson13, Conjecture 3.10]) which generalises Theorem 1.1. Our first main result verifies this conjecture and is the following.
Theorem 1.2. For any
$A\subset {\mathbb N}$
with positive upper Banach density and
$\ell ,m \in {\mathbb N}$
, there exists some infinite set
$B\subset {\mathbb N}$
and a number
$t\in {\mathbb N}$
such that
$$ \begin{align*}\{mb_1 + \ell b_2\colon b_1,b_2\in B,\ b_1 < b_2\} +t \subset A.\end{align*} $$
Remark 1.3. If
$\ell =m=1$
, Theorem 1.2 coincides with Theorem 1.1 and more generally, when
$\ell =m$
, Theorem 1.2 can easily be deduced from Theorem 1.1. If
$\ell \neq m$
, shifts of the patterns
$\{mb_1 + \ell b_2\colon b_1,b_2\in B,\ b_1 \neq b_2\}$
can not always be found in sets of positive density. In fact, these sumsets are not even partition regular as shown in [Reference Kra, Moreira, Richter and Robertson13, Example
$3.9$
].
Our proof of Theorem 1.2 is ergodic-theoretic in nature. The main setup for it is laid out in Section 3 and it is completed in Section 4, along with a slightly stronger result (see Remark 4.3).
For the purposes of contextualising our next main results, we redirect our attention to Theorem 1.1. In particular, we point out that the restriction
$b_1\neq b_2$
is necessary and it was long known that there exist sets of full upper Banach density not containing infinite sumsets
$\{b_1+b_2: b_1,b_2 \in B\}$
up to shifts (e.g., [Reference Kra, Moreira, Richter and Robertson13, Example 2.3]). A natural question then is whether one can guarantee such unrestricted sumsets in sets which are large through stronger notions of density. Recall that for a set
$A\subset {\mathbb N}$
, its asymptotic upper and lower densities, denoted by
$\overline {\mathop {}\!\mathrm {d}}(A)$
and
$\underline {\mathop {}\!\mathrm {d}}(A)$
respectively, are defined as the limits
$$ \begin{align*}\overline{\mathop{}\!\mathrm{d}}(A)=\limsup_{N\to \infty} \frac{|A \cap \{1,\ldots,N\}}{N}\quad \text{and}\quad \underline{\mathop{}\!\mathrm{d}}(A)= \liminf_{N\to \infty} \frac{|A \cap \{1,\ldots,N\}|}{N}.\end{align*} $$
In [Reference Kousek and Radić12], the author and Radić gave a solution to the unrestricted version of this problem for asymptotic upper and lower density, via the following result.
Theorem 1.4 [Reference Kousek and Radić12, Theorems 1.2, 1.3].
Let
$A \subset {\mathbb N}$
.
-
1. If
$\overline {\mathop {}\!\mathrm {d}}(A)>5/6$
or
$\underline {\mathop {}\!\mathrm {d}}(A)>3/4$
, there exists an infinite set
$B\subset {\mathbb N}$
such that
$B+B \subset A$
. -
2. If
$\overline {\mathop {}\!\mathrm {d}}(A)>2/3$
or
$\underline {\mathop {}\!\mathrm {d}}(A)>1/2$
, there exist an infinite set
$B\subset {\mathbb N}$
and
$t\in \{0,1\}$
such that
$B+B+t \subset A$
.
Remark 1.5. It was also shown in [Reference Kousek and Radić12] that both of these results are optimal in the sense that, for example, there exists
$A\subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)=5/6$
, such that
$B+B\not \subset A$
for any infinite
$B\subset {\mathbb N}$
.
Analogously, we are also interested in an unrestricted version of Theorem 1.2. Including the diagonal in the sumsets is an important first step in this direction. Building on the ideas involved in the proof of Theorem 1.4 and our proof of Theorem 1.2, we are able to prove the following results.
Theorem 1.6. Let
$\ell ,m \in {\mathbb N}$
. For any
$A\subset {\mathbb N}$
with
$\underline {\mathop {}\!\mathrm {d}}(A)>1/2$
, there exist an infinite set
$B\subset {\mathbb N}$
and some
$t\in {\mathbb N}$
such that
$$ \begin{align*}\{mb_1 + \ell b_2\colon b_1,b_2\in B\ \text{and}\ b_1 \leq b_2\} + t \subset A.\end{align*} $$
Theorem 1.7. Let
$\ell ,m \in {\mathbb N}$
and
$k=m/\ell $
. For any
$A\subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)>1-1/(k+2)$
, there exist an infinite set
$B\subset {\mathbb N}$
and some
$t\in {\mathbb N}$
such that
$$ \begin{align*}\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text{and}\ b_1 \leq b_2\} + t \subset A.\end{align*} $$
We will in fact show that both the previous bounds are optimal in the sense of Remark 1.5. We also stress that the bound established in Theorem 1.6 does not depend on the parameters
$m,\ell $
, unlike the bound in Theorem 1.7, which does so implicitly, as it depends on the ratio
$m/\ell $
. On another note, it is easy to see that the shift t in Theorems 1.2, 1.6 and 1.7 can be chosen from
$\{0,1,\ldots ,\ell +m-1\}$
. Indeed, write
$t=(\ell +m)j+i$
, for some
$j\in {\mathbb N}_0$
and
$i\in \{0,1,\ldots ,\ell +m-1\}$
. Then, for example, the inclusion
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\} + t \subset A$
can be rewritten as
$\{mb_1 + \ell b_2 : b_1,b_2 \in (B+j)\ \text {and}\ b_1 \leq b_2\} + i \subset A$
.
We also prove similar results for the case of unshifted patterns.
Theorem 1.8. Let
$\ell ,m \in {\mathbb N}$
and
$k=m/\ell .$
For any
$A\subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)>1-1/\left (\ell (k+1)(k+2)\right )$
, there exists an infinite set
$B\subset {\mathbb N}$
such that
$$ \begin{align*}\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text{and}\ b_1 \leq b_2\} \subset A.\end{align*} $$
In Section 5 we prove that Theorems 1.7 and 1.8 are optimal in the sense of Remark 1.5. An analogue of Theorem 1.8 with lower density threshold of
$\underline {\mathop {}\!\mathrm {d}}(A)>1-1/(2(\ell +m))$
is proven in Section 6, where we also show that this and Theorem 1.6 are optimal. For a discussion about other potential unrestricted versions of Theorem 1.2 we refer the reader to Section 7.
Our proofs of the above results use ergodic theory. Expanding on the ideas introduced in [Reference Kra, Moreira, Richter and Robertson15], given a set
$A\subset {\mathbb N}$
, we first relate the inclusion
$\{mb_1 + \ell b_2\colon b_1,b_2\in B\ \text {and}\ b_1 < b_2\} + t \subset A$
to the existence of a specific system
$(X,\mu , T)$
, and a triple
$(a,x_1,x_2) \in X^3$
, with predetermined
$a\in X$
, such that
$\left ( T^{\ell } \times T^m \right ) ^{n_i} \left ( a, x_1 \right ) \to (x_1,x_2)$
, along a sequence
$(n_i)_{i \in {\mathbb N}}$
. In Section 2.1 we explain how a classical version of Furstenberg’s correspondence principle allows us to translate Theorem 1.2 to a dynamical statement of the above form, that is, Theorem 2.2.
The problem gets more complicated – already at the level of the correspondence principle – if we also want to include the diagonal in the sumsets. More precisely, in the above dynamical setting, in order to guarantee that
$\{ mb_1 + \ell b_2\colon b_1,b_2\in B\ \text {and}\ b_1 \leq b_2\}+t \subset A$
, we additionally need to know that
$(T^{j \ell })^{n_i}a \to x_2$
, for some
$j\in {\mathbb N}$
such that
$j\ell =\ell +m$
. However, this equation is only solvable if
$k=m/\ell $
is an integer. In this special case, one could devise a modified version of the correspondence principle, by building an appropriate
$(T^{(k+1)}\times T)$
-invariant probability measure in
$(\{0,1\}^{{\mathbb Z}} \times \{0,1\}^{{\mathbb Z}}, T^{(k+1)} \times T)$
. For the case
$\ell =m=1$
, this argument was utilised in [Reference Kousek and Radić12].
To handle the general case when the ratio
$k=m/\ell $
is not necessarily an integer, we consider a
$(T^{(\lceil k \rceil +1)}\times T)$
-invariant probability measure in
$(\{0,1\}^{{\mathbb Z}} \times \{0,1\}^{{\mathbb Z}}, T^{(\lceil k \rceil +1)} \times T)$
, where
$\lceil k \rceil $
denotes the ceiling of k, arising from a generic pair of points
$(a',a)$
, where a corresponds to the indicator of A, and
$a'$
corresponds to the indicator of an auxiliary set
$A'\subset {\mathbb N}$
. Essentially,
$A'$
is such that the inclusion
$\ell (\lceil k \rceil +1)B+t \subset A'$
also implies
$(m+\ell )B + t \subset A$
. In Section 2.2 we formulate this version of the correspondence principle as Lemma 2.8 and use it in order to deduce Theorem 1.7 from a dynamical statement, namely Theorem 2.6. The proof of Lemma 2.8, along with that of another correspondence principle which is used for the case of unshifted patterns
$\{ mb_1 + \ell b_2\colon b_1,b_2\in B\ \text {and}\ b_1 \leq b_2\}$
, is given in Section 3.5.
One cannot overestimate the influence of the pioneering work presented in [Reference Kra, Moreira, Richter and Robertson15] on recent results pertaining to the ergodic theory approach to infinite sumsets. For work related to this interesting and flourishing theory see [Reference Ackelsberg1], [Reference Charamaras and Mountakis3], [Reference Di Nasso, Goldbring, Jin, Leth, Lupini and Mahlburg4], [Reference Host9], [Reference Kra, Moreira, Richter and Robertson14], [Reference Moreira, Richter and Robertson17] (other infinite sumset results via different methods can be found in [Reference Granville7], [Reference Maynard16], [Reference Tao and Ziegler18]).
Noteworthily, it was privately communicated to the author that Felipe Hernández has independently found a (different) proof of Theorem 1.2 (which has now been published [Reference Hernández8], after the first preprint of this article appeared).
2 Translation to dynamics
2.1 Restricted sumsets
For the reader’s convenience we recall some standard concepts. A topological system is a pair
$(X,T)$
, where X is a compact metric space and
$T\colon X \to X$
a homeomorphism. Whenever there is a T-invariant Borel probability measure
$\mu $
on X, we call
$(X,\mu ,T)$
a measure-preserving system.
The system
$(X,\mu ,T)$
is ergodic if the only T-invariant sets have either measure
$0$
or
$1$
. We denote the support of the measure
$\mu $
, which is defined as the smallest closed subset of X with full measure, by
$\operatorname {supp}(\mu )$
.
Given a measure-preserving system
$(X,\mu ,T)$
, a function
$f\in L^2(X)$
is called weak-mixing if
$$ \begin{align*}\lim_{N\to \infty} \frac{1}{N} \sum_{n=1}^N \left| \int_X T^nf \cdot \bar{f}\ d\mu \right| =0.\end{align*} $$
A Følner sequence
$\Phi $
in
${\mathbb N}$
is a sequence of (nonempty) finite sets
$N \mapsto \Phi _N \subset {\mathbb N}$
,
$N\in {\mathbb N}$
such that
$$ \begin{align*}\lim_{N\to \infty} \frac{\left| \Phi_N \cap \left(t+\Phi_N\right) \right|}{|\Phi_N|}=1,\end{align*} $$
for any
$t\in {\mathbb N}$
. Given a system
$(X,\mu ,T)$
, a point
$a\in X$
is T-generic for
$\mu $
along a Følner sequence
$\Phi $
, written as
$a\in \textbf {gen}(\mu , T, \Phi )$
, or simply
$a\in \textbf {gen}(\mu , \Phi )$
when there is no danger of confusion, if
$$ \begin{align*}\mu = \lim_{N\to \infty} \frac{1}{|\Phi_N|} \sum_{n\in \Phi_N } \delta_{T^n a},\end{align*} $$
where
$\delta _x$
is the Dirac mass at
$x\in X$
and the limit is in the weak* topology.
We next define the concept of dynamical progressions – which parallels that of Erdős progressions introduced in [Reference Kra, Moreira, Richter and Robertson15] – which as we shall see are connected to the combinatorial patterns that we are looking for in Theorem 1.2.
Definition 2.1. Given a topological system
$(X,T)$
and natural numbers
$\ell ,m$
, we say that a point
$(x_0,x_1,x_3)\in X^3$
is an
$(\ell ,m)$
-Erdős progression if there exists a sequence
$n_1<n_2<\cdots $
of integers such that
$(T^{\ell } \times T^m)^{n_i}(x_0,x_1) \xrightarrow {} (x_1,x_2)$
as
$i\to \infty $
.
Our first main dynamical result, the one behind Theorem 1.2, is the following theorem.
Theorem 2.2. Let
$(X,\mu ,T)$
be an ergodic system, let
$a\in \textbf {gen}(\mu ,T,\Phi )$
for some Følner sequence
$\Phi $
and
$E \subset X$
be an open set with
$\mu (E)>0$
. Then, for each
$\ell ,m\in {\mathbb N}$
, there exist
$x_1,x_2 \in X$
and
$t\in {\mathbb N}$
so that
$(a,x_1,x_2) \in X^3$
is an
$(\ell ,m)$
-Erdős progression and
$T^tx_2 \in E$
.
It turns out that Theorems 1.2 and 2.2 are actually equivalent, but we shall only deal with the required direction here. For this we need the following – parallel of [Reference Kra, Moreira, Richter and Robertson15, Theorem
$2.2$
] – result.
Proposition 2.3. Fix a topological system
$(X,T)$
and open sets
$U,V \subset X$
. If there exists an
$(\ell ,m)$
-Erdős progression
$(x_0,x_1,x_2)\in X^3$
with
$x_1\in U$
and
$x_2 \in V$
, then there exists some infinite set
$B\subset \{n\in {\mathbb N}\colon T^{\ell n}x_0 \in U\}$
such that
$\{mb_1+\ell b_2\colon b_1,b_2\in B,\ b_1<b_2\} \subset \{n\in {\mathbb N}\colon T^nx_0 \in V\}$
.
Proof. By the definition of
$(\ell ,m)$
-Erdős progressions we can find a strictly increasing sequence
$(c_n)_{n\in {\mathbb N}}$
such that
$(T^{\ell } \times T^m)^{c_n}(x_0,x_1) \xrightarrow {} (x_1,x_2)$
as
$n\to \infty $
and each
$c_n$
is such that
$T^{\ell c_n}x_0 \in U$
. We will construct
$B \subset \{c_n: n\in {\mathbb N}\}$
inductively and, the basis of the induction being simple, we only prove the inductive step. Suppose
$b_1<\dots < b_n$
have been chosen so that
$$ \begin{align*}x_0 \in \bigcap_{1\leq i < j \leq n} T^{-mb_i -\ell b_j}V\ \text{and}\ x_1\in \bigcap_{1\leq i \leq n} T^{-m b_i}V.\end{align*} $$
Then, we can choose
$b_{n+1} \in \{c_k: k \in {\mathbb N}\}$
with
$b_{n+1}>b_n$
and such that
$$ \begin{align*}(T^{\ell} \times T^m)^{b_{n+1}}(x_0,x_1) \in \left( \bigcap_{1\leq i \leq n} T^{-m b_i}V \right) \times V.\end{align*} $$
It follows that
$$ \begin{align*}x_0 \in \bigcap_{1\leq i < j \leq n+1} T^{-mb_i -\ell b_j}V\ \text{and}\ x_1\in \bigcap_{1\leq i \leq n+1} T^{-m b_i}V\end{align*} $$
and this concludes the induction. We finish the proof by letting
$B=\{b_n: n\in {\mathbb N}\}$
.
To prove that Theorem 2.2 implies Theorem 1.2 we shall use the following classical version of Furstenberg’s correspondence principle.
Lemma 2.4 [Reference Kra, Moreira, Richter and Robertson14, Theorem 2.10].
For a set
$A\subset {\mathbb N}$
with
$\mathop {}\!\mathrm {d}^{*}(A)>0$
there exists an ergodic system
$(X,\mu ,T)$
, a Følner sequence
$\Phi $
, a point
$a\in \texttt {gen}(\mu ,T,\Phi )$
and a clopen set
$E\subset X$
such that
$\mu (E)>0$
and
$A=\{n\in {\mathbb N}: T^na \in E\}$
.
Proof that Theorem 2.2 implies Theorem 1.2.
Let
$A \subset {\mathbb N}$
with
$\mathop {}\!\mathrm {d}^{*}(A)>0$
and
$(X,\mu ,T)$
,
$a\in X$
,
$\Phi $
and
$E\subset X$
be those arising from Lemma 2.4. By Theorem 2.2, there exists a
$t\in {\mathbb N}$
and an
$(\ell , m)$
-Erdős progression
$(a,x_1,x_2) \in \{a\} \times X \times T^{-t}E$
. Invoking Proposition 2.3 we obtain an infinite set
$B\subset {\mathbb N}$
, such that
$\{mb_1+\ell b_2\colon b_1,b_2\in B,\ b_1<b_2\} \subset \{n\in {\mathbb N}\colon T^na \in T^{-t}E\}$
. Since
$A=\{n\in {\mathbb N}: T^na \in E\}$
, we see that
$A-t=\{n\in {\mathbb N}\colon T^na \in T^{-t}E\}$
, so the theorem follows.
Apropos of this discussion, we address the necessity of the shift in Theorem 1.2 and also the density threshold for the unshifted version. This is merely an observation, but for the reader’s convenience we prove it in the next proposition.
Proposition 2.5. Let
$\ell ,m\in {\mathbb N}$
. If
$A\subset {\mathbb N}$
with
$\mathop {}\!\mathrm {d}^{*}(A)>1-\frac {1}{(\ell +m)}$
, then there is an infinite set
$B\subset {\mathbb N}$
such that
$$ \begin{align*}\{mb_1 + \ell b_2\colon b_1,b_2\in B,\ b_1 < b_2\} \subset A.\end{align*} $$
Otherwise, the shift in Theorem 1.2 is in general necessary.
Proof. Observe that the set
$A={\mathbb N} \setminus (\ell +m){\mathbb N}$
has natural density
$1-\frac {1}{(\ell +m)}$
and contains no infinite sumset of the form
$\{mb_1 + \ell b_2\colon b_1,b_2\in B,\ b_1 < b_2\}$
. Indeed, the infinity of B allows us to choose an infinite subset of it, say
$B'\subset B$
, all the elements of which are equal modulo
$(\ell +m)$
. That is, there is some
$j\in \{0,1,\ldots ,\ell +m-1\}$
so that any
$b\in B'$
is of the form
$b=(\ell +m)n+j$
, some
$n\in {\mathbb N}$
. It follows that
$mb_1+\ell b_2 \in (\ell +m){\mathbb N}$
, for any
$b_1,b_2\in B'$
. This means that the shift above is necessary and the density threshold cannot be improved.
On the other hand, if
$A\subset {\mathbb N}$
with
$\mathop {}\!\mathrm {d}^{*}(A)>1-\frac {1}{(\ell +m)}$
, it is easy to see that
$\mathop {}\!\mathrm {d}^{*}(A\cap (\ell +m){\mathbb N})>0$
and then by Theorem 1.2 there is some infinite
$B\subset {\mathbb N}$
such that
$$ \begin{align*}\{mb_1 + \ell b_2\colon b_1,b_2\in B,\ b_1 < b_2\} \subset A\cap (\ell+m){\mathbb N} \subset A.\end{align*} $$
Again, for the first inclusion we implicitly used the fact that infinity of B allows us to choose an infinite subset of it, all the elements of which are equal modulo
$(\ell +m)$
.
2.2 Lifting restrictions
In order to prove the combinatorial results in Theorems 1.7 and 1.8 we will use the following dynamical results respectively. Recall that for a real number
$r\in {\mathbb R}$
,
$\lceil r \rceil \in {\mathbb Z}$
denotes its ceiling.
Theorem 2.6. Let
$(X,\mu ,T)$
be an ergodic system and
$a\in \textbf {gen}(\mu ,\Phi )$
for some Følner sequence
$\Phi $
. Moreover, let
$\ell ,m\in {\mathbb N}$
,
$q=\lceil m/\ell \rceil $
and assume that
$E_1,\ldots ,E_{\ell +m},F_1,\ldots ,F_{\ell +m}\subset X$
are open sets such that
$F_j=T^{-(j-1)}F_1$
,
$j=1,\ldots ,\ell +m$
,
$E_{i+(q+1)}=T^{-1}E_i$
, for
$i=1,\ldots ,\ell +m-q-1$
, and also
$$ \begin{align} (\ell+m)\mu(F_1)+\ell \left(\mu(E_1)+\cdots + \mu(E_{q+1}) \right)>\ell(q+1). \end{align} $$
Then, for some
$j\in \{1,\ldots ,\ell +m\}$
, there exist
$x_1,x_2 \in X$
so that
$(a,x_1,x_2) \in X^3$
is an
$(\ell ,m)$
-Erdős progression and
$(x_1,x_2) \in E_j \times F_j$
.
Theorem 2.7. Let
$(X,\mu ,T)$
be an ergodic system, let
$a\in \textbf {gen}(\mu ,\Phi )$
for some Følner sequence
$\Phi $
and
$E,F \subset X$
be open sets with
$$ \begin{align} (\ell+m)\mu(F)+\ell\mu(E)>2\ell+m-1, \end{align} $$
for some
$\ell ,m \in {\mathbb N}$
. Then, there exist
$x_1,x_2 \in X$
such that
$(a,x_1,x_2) \in X^3$
is an
$(\ell ,m)$
-Erdős progression and also
$(x_1,x_2) \in E \times F$
.
To facilitate the transition from ergodic theory to combinatorics in this setting, we shall again utilise the notion of
$(\ell ,m)-$
Erdős progressions as in Definition 2.1, as well as Proposition 2.3. However, the previously used, more classical version of Furstenberg’s correspondence principle seems to no longer be useful and we need the adaptations presented in Lemmas 2.8 and 2.9 below, for Theorems 1.7 and 1.8, respectively.
Before stating the lemmas, we establish some notation;
$\Sigma $
denotes the space
$\{0,1\}^{{\mathbb Z}}$
and is endowed with the product topology so that it is compact metrizable. We also let
$S \colon \Sigma \to \Sigma $
denote the shift transformation given by
$S(x(n))=x(n+1)$
, for any
$n\in {\mathbb Z}$
,
$x=(x(n))_{n\in {\mathbb Z}} \in \Sigma $
.
Lemma 2.8. Let
$A\subset {\mathbb N}$
and
$\ell ,m \in {\mathbb N}$
with
$k=m/\ell $
and let
$q=\lceil k \rceil $
. Then, there exist an ergodic system
$(\Sigma \times \Sigma , \mu , S^{(q+1)} \times S)$
, an open set
$E\subset \Sigma $
, a pair of points
$a,a'\in \Sigma $
and a Følner sequence
$\Phi $
, such that
$(a',a)\in \textbf {gen}(\mu ,\Phi )$
and
$$ \begin{align*} (\ell+m)\mu(\Sigma \times E) + \ell \sum_{j=0}^{q} \mu(S^{-j}E \times \Sigma) \geq (\ell+m) \left((k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A)-k \right)+\ell (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A) + \ell(q-k). \end{align*} $$
It also holds that
$A=\{n\in {\mathbb N}: S^n a \in E \}$
and
$(A-j)/(\ell +m ) =\{n\in {\mathbb N}: S^{(q+1)\ell n+j}a' \in E\}$
, for each
$j=0,1,\dots ,\ell +m -1$
, where
$(A-j)/(\ell +m )=\{n\in {\mathbb N}: n(\ell +m )+j\in A\}$
.
Lemma 2.9. Let
$A\subset {\mathbb N}$
and
$\ell ,m\in {\mathbb N}$
with
$k=m/\ell $
. Then, there exists an ergodic system
$(\Sigma \times \Sigma , \mu , S \times S)$
, an open set
$E\subset \Sigma $
, a pair of points
$a",a\in \Sigma $
and a Følner sequence
$\Phi $
, such that
$(a",a)\in \textbf {gen}(\mu ,\Phi )$
and
$$ \begin{align*} (\ell+m)\mu(\Sigma \times E) + \ell \mu(E \times \Sigma) \geq (2\ell+m)\left( (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A) - k \right). \end{align*} $$
It also holds that
$A = \{ n \in {\mathbb N}: S^n a \in E \}$
and
$A/(\ell +m ) =\{n\in {\mathbb N}: S^{\ell n}a" \in E\}$
.
We postpone the proofs of Lemmas 2.8 and 2.9 until the end of Section 3. Instead, we will finish this section by showing how to deduce Theorems 1.7 and 1.8 from their dynamical counterparts, using the tools we have acquired thus far. To this end, we reverse the order of presentation and start with the case of no shift because the proof is, at the very least notationally, lighter.
Proof that Theorem 2.7 implies Theorem 1.8.
Let
$\ell ,m \in {\mathbb N}$
and let
$k=m/\ell $
. Given
$A\subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)>1-1/\left (\ell (k+1)(k+2)\right )$
, we find, by way of Lemma 2.9, an ergodic system
$(\Sigma \times \Sigma , \mu , S \times S)$
, an open set
$E\subset \Sigma $
, a pair of points
$a",a\in \Sigma $
satisfying the conditions of Lemma 2.9 and a Følner sequence
$\Phi $
, such that
$(a",a)\in \textbf {gen}(\mu ,\Phi )$
and
$$ \begin{align*} (\ell+m)\mu(\Sigma \times E) + \ell \mu(E \times \Sigma) \geq (2\ell+m) \left( (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A)-k \right)>(2\ell+m)(1-\frac{1}{\ell(k+2)})=2\ell+m-1, \end{align*} $$
because
$\ell +m=\ell (k+1)$
, hence
$\ell (k+2)=2\ell +m$
. It follows by Theorem 2.7 that there exist some points
$(x_{10},x_{11}),(x_{20},x_{21}) \in \Sigma \times \Sigma $
so that
$((a",a),(x_{10},x_{11}),(x_{20},x_{21})) \in (\Sigma \times \Sigma )^3$
is an
$(\ell ,m)$
-Erdős progression for
$(\Sigma \times \Sigma , \mu , S \times S)$
and
$((x_{10},x_{11}),(x_{20},x_{21})) \in (E\times \Sigma ) \times (\Sigma \times E)$
. Then, an application of Proposition 2.3 yields an infinite set
$B\subset {\mathbb N}$
such that
$$ \begin{align*}B\subset \{n\in {\mathbb N}: (S \times S)^{\ell n}(a",a) \in E\times \Sigma \}= \{n\in {\mathbb N}: S^{\ell n}a" \in E \}\end{align*} $$
and similarly,
$$ \begin{align*}\{ mb_1+\ell b_2: b_1,b_2\in B\ \text{and}\ b_1<b_2\} \subset \{n\in {\mathbb N}: (S \times S)^{n}(a,a) \in \Sigma \times E \}=\{n\in {\mathbb N}: S^na \in E \}.\end{align*} $$
Since
$S^{\ell n}a"\in E\iff (\ell +m) n\in A$
, the former inclusion rewrites as
$(\ell +m)B \subset A$
and the latter as
$\{ mb_1+\ell b_2: b_1,b_2\in B\ \text {and}\ b_1<b_2\} \subset A$
. Combining these two we conclude that
$\{mb_1+\ell b_2: b_1,b_2\in B\ \text {and}\ b_1\leq b_2\} \subset A$
.
Proof that Theorem 2.6 implies Theorem 1.7.
Let
$m,\ell \in {\mathbb N}$
and
$k=m/\ell $
,
$q=\lceil k \rceil $
. Given
$A\subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)>(k+1)/(k+2)$
, we find, by way of Lemma 2.8, an ergodic system
$(\Sigma \times \Sigma , \mu , S^{(q+1)} \times S)$
, an open set
$E\subset \Sigma $
, a pair of points
$a',a\in \Sigma $
satisfying the conditions in Lemma 2.8 and a Følner sequence
$\Phi $
, such that
$(a',a)\in \textbf {gen}(\mu ,\Phi )$
and
$$ \begin{align*} & (\ell+m)\mu(\Sigma \times E) + \ell \sum_{j=0}^{q} \mu(S^{-j}E \times \Sigma) \geq (2\ell+m) (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A) + \ell(q-k) -(\ell+m)k>\\ & (2\ell+m)(k+1)\frac{k+1}{k+2}+\ell(q-k)-\ell(k+1)k=\ell(k+1)(k+1)+\ell(q-k)-\ell(k+1)k=\ell(q+1), \end{align*} $$
We now justify why Theorem 2.6 applies in order for us to recover an
$(\ell ,m)$
-Erdős progression
$\left ( (a',a),(x_{10},x_{11}) , (x_{20},x_{21}) \right ) \in (\Sigma \times \Sigma )^3$
, with
$$ \begin{align*}(x_{10},x_{11}, x_{20},x_{21}) \in E_j \times F_j=S^{-(j-1)}E \times \Sigma \times \Sigma \times S^{-(j-1)}E,\end{align*} $$
for some
$j\in \{1,2,\dots ,\ell +m \}$
. To see this, note that
$E_j=S^{-(j-1)}E\times S$
and so
$E_{j+(q+1)}=(S^{(q+1)}\times S)^{-1}E_j$
, for
$j\in \{1,\ldots ,\ell +m-q-1\}$
. Moreover we showed above that
$$ \begin{align*}(\ell+m)\mu(\Sigma \times E) + \ell \sum_{j=0}^{q} \mu(S^{-j}E \times \Sigma)> \ell(q+1),\end{align*} $$
which is precisely (2.1). Then, using Proposition 2.3 we find an infinite set
$B\subset {\mathbb N}$
such that
$$ \begin{align*}B\subset \{n\in {\mathbb N}: S^{(q+1)\ell n}a' \in S^{-(j-1)}E \}\end{align*} $$
and
$$ \begin{align*}\{ mb_1+\ell b_2: b_1,b_2\in B\ \text{and}\ b_1<b_2\} \subset \{n\in {\mathbb N}: S^na \in S^{-(j-1)}E \},\end{align*} $$
for some
$j\in \{1,\ldots ,\ell +m\}$
. From the defining properties of
$a'$
, we see that the former becomes
$B \subset (A-(j-1))/(\ell +m ).$
Thus, unraveling the definitions, we see that these two inclusions together translate to
$$ \begin{align*}\{mb_1+\ell b_2: b_1,b_2\in B\ \text{and}\ b_1\leq b_2\} \subset A-(j-1),\end{align*} $$
and so we conclude.
3 The ergodic theory setup
3.1 An overview
A sufficient condition for a triple
$(x_0,x_1,x_2) \in X^3$
to be an
$(\ell ,m)$
-Erdős progression is that
$(x_0,x_1)$
is a
$(T^{\ell } \times T^m)$
-generic point for some invariant measure and
$(x_1,x_2) \in X\times X$
is in the support of that measure. This is a general fact which can easily be deduced from the definitions (see, e.g., [Reference Kra, Moreira, Richter and Robertson14, Lemma 2.4]). A well-known consequence of the mean ergodic theorem is that for an ergodic system
$(Y,\nu ,S)$
and any Følner sequence, there is a subsequence
$\Phi $
such that
$\nu $
-almost every point
$y\in Y$
is S-generic along
$\Phi $
. Hence, if in the above setting
$\mu $
is a T-invariant measure, we want to consider an ergodic decomposition of
$\mu \times \mu $
.
As in [Reference Kra, Moreira, Richter and Robertson15] we are interested in progressions with prescribed first coordinate
$a\in X$
and so we will reduce to the case that the ergodic decomposition is continuous. However, our work is different here because we need typical points to be
$(T^{\ell } \times T^m)$
-generic for general
$\ell ,m \in {\mathbb N}$
. Another important aspect of this problem is that the linear patterns we are looking for are still dynamically controlled by the Kronecker factor. Therefore, we find it useful to introduce a measure
$\sigma $
on
$X\times X$
which gives full measure to the set of points
$(x_1,x_2)$
such that
$(a,x_1,x_2)$
projects to an
$(\ell ,m)$
-three term progression on the Kronecker, in a way similar to that done in [Reference Kra, Moreira, Richter and Robertson15] for the case
$\ell =m=1$
.
3.2 Continuous ergodic decomposition
To proceed with the constructions we briefly recall some standard notions. If
$(X,\mu ,T)$
and
$(Y,\nu ,S)$
are two systems, a measurable map
$\pi \colon X \to Y$
for which
$\pi \mu = \nu $
andFootnote
1
$$ \begin{align} \pi \circ T = S \circ \pi \quad \mu \text{-almost everywhere} \end{align} $$
is called a factor map. If, in addition,
$\pi $
is continuous, surjective and (3.1) holds everywhere we call
$\pi $
a continuous factor map. Note that factors of ergodic systems are also ergodic. Given a factor map
$\pi : X\to Y$
and a function
$f\in L^2(X,\mu )$
, we write
$\mathbb {E}(f | Y)$
for the conditional expectation
$\mathbb {E}(f | \pi ^{-1}\mathcal {B}(Y))$
, where
$\mathcal {B}(Y)$
is the Borel
$\sigma $
-algebra on Y.
A group rotation is a system
$(Z,\nu ,R)$
, for a compact abelian group Z with its normalised Haar measure
$\nu $
and
$R\colon Z \to Z$
being a rotation of the form
$R(z)=z+b$
, some
$b \in Z$
. In this case we can also assume that the compatible metric on Z is such that
$z \mapsto z+w$
is an isometry for all
$w\in Z$
.
Every ergodic system has a maximal group rotation factor, called the Kronecker factor, and while in general the factor map from an ergodic system
$(X,\mu ,T)$
to its Kronecker
$(Z,\nu ,R)$
is only measurable, for our purposes we may assume that it is also a continuous surjection. Indeed, using Proposition
$3.20$
from [Reference Kra, Moreira, Richter and Robertson14] one can show that Theorem 2.2 follows from the next seemingly weaker result. The proof of this implication is the same as the proof that Theorem
$3.2$
implies Theorem
$1.4$
in [Reference Kra, Moreira, Richter and Robertson15] or the proof of Theorem
$2.1$
via Theorem
$3.4$
in [Reference Kousek and Radić12].
Theorem 3.1. Let
$(X,\mu ,T)$
be an ergodic system and assume there is a continuous factor map
$\pi $
to its Kronecker. Let
$a\in \textbf {gen}(\mu ,T,\Phi )$
, for some Følner sequence
$\Phi $
and
$E \subset X$
be an open set with
$\mu (E)>0$
. Then, there exist
$x_1,x_2\in X$
and
$t\in {\mathbb N}$
so that
$(a,x_1,x_2)\in X^3$
is an
$(\ell , m)$
-Erdős progression such that
$T^tx_2 \in E$
.
In a similar fashion, Theorems 2.6 and 2.7 follow from the next seemingly weaker results, respectively, where the system is assumed to have a continuous Kronecker factor map (essentially, the proof of Theorem
$2.1$
from Theorem
$3.4$
in [Reference Kousek and Radić12] contains one of the analogous arguments in the case
$m=\ell =1$
).
Theorem 3.2. Let
$(X,\mu ,T)$
be an ergodic system and assume there is a continuous factor map
$\pi $
to its Kronecker and
$a\in \textbf {gen}(\mu ,T,\Phi )$
for some Følner sequence
$\Phi $
. Moreover, let
$\ell ,m\in {\mathbb N}$
,
$q=\lceil m/\ell \rceil $
and assume that
$E_1,\ldots ,E_{\ell +m},F_1,\ldots ,F_{\ell +m}\subset X$
are open sets such that
$F_j=T^{-(j-1)}F_1$
,
$j=1,\ldots ,\ell +m$
,
$E_{i+(q+1)}=T^{-1}E_i$
, for
$i=1,\ldots ,\ell +m-q-1$
, and also
$$ \begin{align} (\ell+m)\mu(F_1)+\ell \left(\mu(E_1)+\cdots + \mu(E_{q+1}) \right)>\ell(q+1). \end{align} $$
Then, for some
$j\in \{1,\ldots ,\ell +m\}$
, there exist
$x_1,x_2 \in X$
so that
$(a,x_1,x_2) \in X^3$
is an
$(\ell ,m)$
-Erdős progression and
$(x_1,x_2) \in E_j \times F_j$
.
Theorem 3.3. Let
$(X,\mu ,T)$
be an ergodic system and assume there is a continuous factor map
$\pi $
to its Kronecker. Let
$a\in \textbf {gen}(\mu ,T,\Phi )$
for some Følner sequence
$\Phi $
and
$E,F \subset X$
be open sets with
$$ \begin{align} (\ell+m)\mu(F)+\ell\mu(E)>2\ell+m-1. \end{align} $$
Then, there exist
$x_1,x_2 \in X$
so that
$(a,x_1,x_2) \in X^3$
is an
$(\ell ,m)$
-Erdős progression and
$(x_1,x_2) \in E \times F$
.
We fix
$\ell ,m\in {\mathbb N}$
and an ergodic system
$(X,\mu ,T)$
with a continuous factor map
$\pi $
to its Kronecker
$(Z,\nu ,R)$
. We also fix a disintegration
$z \mapsto \eta _z$
of
$\mu $
over the Kronecker (for details, see, e.g., [Reference Einsiedler and Ward5, Theorem
$5.14$
]). Then, for every
$(x_1,x_2)\in X \times X $
we define the measure
$$ \begin{align} \lambda_{(x_1,x_2)}=\int_Z \eta_{\ell z+\pi(x_1)} \times \eta_{mz + \pi(x_2)}\ d\nu(z) \end{align} $$
on
$X\times X$
. We stress that (3.4) is well-defined since, for each
$(x_1,x_2) \in X\times X$
the measures
$\eta _{\ell z + \pi (x_1)}$
and
$\eta _{mz+\pi (x_2)}$
are defined for
$\nu $
-almost every
$z\in Z$
. Note that, because of the ergodicity of R, the subgroups
$\ell Z$
and
$mZ$
of Z both have positive measure (see the proof of Lemma 3.7 for more details on this). We next examine some properties of this (a posteriori) disintegration of
$\mu \times \mu $
.
Proposition 3.4. In the above setting, the map
$(x_1,x_2) \mapsto \lambda _{(x_1,x_2)}$
satisfies the following properties.
-
(i) The map
$(x_1,x_2) \mapsto \lambda _{(x_1,x_2)}$
is continuous. -
(ii) The map
$(x_1,x_2) \mapsto \lambda _{(x_1,x_2)}$
is a disintegration of
$\mu \times \mu $
, meaning that
$$ \begin{align*}\int_{X\times X} \lambda_{(x_1,x_2)}\ d(\mu \times \mu)(x_1,x_2) = \mu \times \mu.\end{align*} $$
-
(iii) For
$(\mu \times \mu )$
-almost every
$(x_1,x_2)\in X\times X$
, the point
$(x_1,x_2)$
is
$(T^{\ell } \times T^m)$
-generic for
$\lambda _{(x_1,x_2)}$
and
$\lambda _{(x_1,x_2)}$
is
$(T^{\ell } \times T^m)$
-ergodic. -
(iv) For every
$(x_1,x_2) \in X\times X$
, we have that
$\lambda _{(x_1,x_2)}=\lambda _{(T^{\ell }x_1,T^mx_2)}.$
The rest of this subsection is devoted to the proof of Proposition 3.4. The first step is a result showing that in some sense the Kronecker is a characteristic factor.
Proposition 3.5. Fix an ergodic system
$(X,\mu ,T)$
with Kronecker factor
$(Z,\nu ,R)$
and factor map
$\pi : X \to Z$
. Then, for any
$\ell ,m \in {\mathbb N}$
and
$f,g\in L^{\infty }(X,\mu )$
we have that
$$ \begin{align} \lim_{N\to \infty} \frac{1}{N} \sum_{n=1}^N f(T^{\ell n}x_0)\cdot g(T^{m n}x_1) = \lim_{N\to \infty} \frac{1}{N} \sum_{n=1}^N \mathbb{E}(f | Z)(R^{\ell n}\pi(x_0)) \cdot \mathbb{E}(g | Z)(R^{m n}\pi(x_1)), \end{align} $$
for
$(\mu \times \mu )$
-almost every
$(x_0,x_1)\in X\times X$
.
Proof. Both limits in (3.5) exist by the pointwise ergodic theorem, so we simply need to establish their equality in the
$L^2$
norm. By the Jacobs-de Leeuw-Glicksberg decomposition (see [Reference Kerr and Li11, Theorem
$2.24$
]) this reduces to showing that whenever either f or g is a weak-mixing function, then
$$ \begin{align} \lim_{N\to \infty} \frac{1}{N}\sum_{n=1}^N T^{\ell n}f \otimes T^{m n}g =0, \end{align} $$
in
$L^2(\mu \times \mu )$
. Assuming, without loss of generality, that f is the weak-mixing function and setting
$u_n=T^{\ell n}f \otimes T^{m n}g$
this follows directly by the van der Corput lemma (originally proven in this version in [Reference Bergelson2, Theorem
$1.4$
]), for
which goes to
$0$
as
$K\to \infty $
by the definition of weak-mixing functions and the inequality
$$ \begin{align*}\frac{1}{K}\sum_{k=1}^K \left| \int_X T^{\ell k}f \cdot \overline{f}\ d\mu \right| \leq \frac{\ell}{\ell K}\sum_{k=1}^{\ell K} \left| \int_X T^{ k}f \cdot \overline{f}\ d\mu \right|.\\[-46pt]\end{align*} $$
We are now in the position to prove the main result of this subsection.
Proof of Proposition 3.4.
We begin by showing the map
$(x_1,x_2) \mapsto \lambda _{(x_1,x_2)}$
is a disintegration of
$\mu \times \mu $
. Let
$f,g\in L^{\infty }(\mu )$
. Then,
$$ \begin{align*} & \int_{X^2} f\otimes g\ d\lambda_{(x_1,x_2)} d(\mu\times \mu)(x_1,x_2) = \int_{X^2} \int_{Z} \int_{X} f\ d\eta_{\ell z+\pi(x_1)} \int_X g\ d\eta_{mz+\pi(x_2)}\ d\nu(z) d\mu(x_1) d\mu(x_2) \\ & = \int_Z \left( \int_X \int_{X} f\ d\eta_{\ell z+\pi(x_1)}\ d\mu(x_1) \times \int_X \int_{X} g\ d\eta_{m z+\pi(x_2)}\ d\mu(x_2) \right)\ d\nu(z) \\ & = \int_Z \left( \int_{X} f\ d\mu \times \int_{X} g\ d\mu\ \right)\ d\nu(z) = \int f\otimes g\ d(\mu\times \mu), \end{align*} $$
because of (3.4) and the fact that for each
$w\in Z$
,
$$ \begin{align*}\mu =\int_Z \eta_z\ d\nu(z) = \int_Z \eta_z\ d(\pi \mu)(z) = \int_X \eta_{\pi(x)}\ d\mu(x) = \int_X \eta_{w+\pi(x)}\ d\mu(x).\end{align*} $$
Part
$(ii)$
follows by standard approximation arguments using Stone-Weierstrass’ theorem and the Riesz-Markov-Kakutani representation theorem.
To prove that
$(x_1,x_2) \mapsto \lambda _{(x_1,x_2)}$
is continuous we need to show that for each
$F\in C(X\times X)$
, the map
$(x_1,x_2) \mapsto \int _{X\times X} F\ d\lambda _{(x_1,x_2)}$
is continuous, because – implicitly – the topology we endow the space of Borel measures on
$X\times X$
with is the weak* topology. To this end, by another application of Stone-Weierstrass’ theorem, we can assume that
$F\in C(X\times X)$
in the previous is of the form
$f\otimes g$
, for some
$f,g\in C(X)$
. Now, letting
$f,g\in C(Z)$
, these functions are also uniformly continuous (by compactness) and so the map
$$ \begin{align*}(v,w) \mapsto \int_{Z}f(\ell z+v)\ g(mz+w)\ d\nu(z)\end{align*} $$
is continuous. Thus, the density of
$C(Z)$
in
$L^2(Z,m)$
implies the continuity of the analogous map for
$f,g \in L^{2}(Z,m)$
.
Now, if
$f,g\in C(X)$
, we have that
$\mathbb {E}(f|Z), \mathbb {E}(g|Z) \in L^2(Z,m)$
and so we see that
$$ \begin{align*}(x_1,x_2) \mapsto \int_{Z} \mathbb{E}(f|Z)(\ell z+\pi(x_1))\ \mathbb{E}(g|Z)(mz+\pi(x_2))\ d\nu(z)\end{align*} $$
is continuous as the composition of continuous maps. Noting that
$\mathbb {E}[f|Z](z)=\int _{X} f\ d\eta _z$
for
$\nu $
-almost every
$z\in Z$
, we see that
$$ \begin{align} \int_{X\times X} f\otimes g\ d\lambda_{(x_1,x_2)}= \int_{Z} \mathbb{E}(f|Z)(\ell z+\pi(x_1))\ \mathbb{E}(g|Z)(mz+\pi(x_2))\ d\nu(z) \end{align} $$
and so the continuity of
$(x_1,x_2) \mapsto \lambda _{(x_1,x_2)}$
follows.
Property
$(iv)$
is immediate up to null sets because
$\pi \circ T = R\circ \pi $
as
$\pi $
is a factor map and then, the established continuity of the decomposition implies it for all points
$(x_1,x_2) \in X\times X$
.
We are only left with proving that
$(x_1,x_2) \mapsto \lambda _{(x_1,x_2)}$
is a
$(T^\ell \times T^m)-$
ergodic decomposition of
$\mu \times \mu $
, because then part
$(iii)$
follows as a consequence of the pointwise ergodic theorem (see, e.g., [Reference Kra, Moreira, Richter and Robertson14, Corollary
$2.9$
]). In other words, we have to show that for each bounded and measurable
${F: X\times X \to {\mathbb C}}$
it holds that
$$ \begin{align*}\int_{X\times X} F\ d\lambda_{(x_1,x_2)} = \mathbb{E}(F | \mathcal{I})(x_1,x_2),\end{align*} $$
for
$(\mu \times \mu )-$
almost every
$(x_1,x_2)\in X\times X$
, where
$\mathcal {I}$
denotes the
$\sigma $
-algebra of
$(T^{\ell }\times T^m)-$
invariant sets on
$X\times X$
. By the ergodic theorem, this is equivalent to showing that
$$ \begin{align*}\lim_{N\to \infty} \frac{1}{N}\sum_{n=1}^N F(T^{\ell n}x_1,T^{mn}x_2)=\int_{X\times X} F\ d\lambda_{(x_1,x_2)},\end{align*} $$
for
$(\mu \times \mu )-$
almost every
$(x_1,x_2)\in X\times X$
and by standard approximation arguments this reduces to showing that
$$ \begin{align*} \lim_{N\to \infty} \frac{1}{N}\sum_{n=1}^N f(T^{\ell n}x_1)\cdot g(T^{mn}x_2)=\int_{X\times X} f\otimes g\ d\lambda_{(x_1,x_2)}, \end{align*} $$
for
$(\mu \times \mu )-$
almost every
$(x_1,x_2)\in X\times X$
and every
$f,g\in L^{\infty }(X,\mu )$
. By (3.5), it suffices to show that
$$ \begin{align} \lim_{N\to \infty} \frac{1}{N} \sum_{n=1}^N \mathbb{E}(f | Z)(R^{\ell n}\pi(x_1)) \cdot \mathbb{E}(g | Z)(R^{m n}\pi(x_2))=\int_{X\times X}\ f\otimes g\ d\lambda_{(x_1,x_2)}, \end{align} $$
for
$(\mu \times \mu )$
-almost every
$(x_1,x_2)\in X\times X$
. As the limit in (3.8) exists almost everywhere, and the dominated convergence theorem applies, it suffices to prove convergence in
$L^2(\mu \times \mu )$
. By (3.7) and the density of (tensor products of) continuous functions in
$L^2(\nu \times \nu )$
it thus suffices to show that
$$ \begin{align} \lim_{N\to \infty} \frac{1}{N} \sum_{n=1}^N \phi_1(R^{\ell n}z_1) \cdot \phi_2(R^{m n}z_2)=\int_{Z}\ \phi_1(\ell z+z_1) \cdot \phi_2(mz+z_2)\ d\nu(z), \end{align} $$
for any
$\phi _1,\phi _2\in C(Z)$
and any
$z_1,z_2\in Z$
.
With this reduction, the algebraic structure of rotations in compact abelian groups (see, e.g., [Reference Host and Kra10, Chapter
$4$
]) allows us to conclude. More precisely, given
$\phi _1,\phi _2\in C(Z)$
and
$z_1,z_2\in Z$
, the function
$\phi : Z \to {\mathbb C}$
given by
$$ \begin{align*}\phi(z)= \phi_1(\ell z+z_1) \cdot \phi_2(mz+z_2)\end{align*} $$
is continuous, and therefore by the unique ergodicity of group rotations we have that
$$ \begin{align*}\lim_{N\to \infty} \frac{1}{N} \sum_{n=1}^N \phi(R^n(0))= \int_Z \phi(z)\ d\nu(z)=\int_Z \phi_1(\ell z+z_1) \cdot \phi_2(mz+z_2)\ d\nu(z).\end{align*} $$
Finally,
$\phi (R^n(0))=\phi _1(R^{\ell n}z_1) \cdot \phi _2(R^{mn}z_2)$
, for each
$n\in {\mathbb N}$
, and thus (3.9) follows.
3.3 A measure on
$(\ell ,m)-$
Erdős progressions and some of its properties
As above,
$(X,\mu ,T)$
is an ergodic system and
$(Z,\nu ,R)$
is its Kronecker factor with (continuous) factor map
$\pi : X \to Z$
, and R is a rotation by some
$b\in Z$
. Moreover, we let
$a\in \textbf {gen}(\mu ,T,\Phi )$
, for some Følner sequence
$\Phi $
. Given
$\ell ,m\in {\mathbb N}$
we consider the measure
$$ \begin{align} \sigma_a= \int_Z \eta_{\ell z+ \pi(a)} \times \eta_{(\ell+m) z + \pi(a)}\ d\nu(z) \end{align} $$
on
$X \times X $
. The first useful property of
$\sigma _a$
which relates to the disintegration
$(x_1,x_2) \mapsto \lambda _{(x_1,x_2)}$
reads as follows.
Lemma 3.6. For
$\sigma _a$
-almost every
$(x_1,x_2) \in X \times X$
it holds that
$\lambda _{(a,x_1)}=\lambda _{(x_1,x_2)}$
.
Proof. It is obvious from the definition of
$\sigma _a$
that the set P defined by
$$ \begin{align*}P=\{(x_1,x_2) \in X\times X \colon \pi(x_1)=\ell w+\pi(a)\ \text{and}\ \pi(x_2)=(\ell+m)w+ \pi(a),\ \text{for some}\ w\in Z\}\end{align*} $$
has
$\sigma _a(P)=1.$
We fix
$(x_1,x_2) \in P$
and let
$w\in Z$
be such that
$\pi (x_1)=\ell w + \pi (a)$
and
$\pi (x_2)=(\ell + m)w + \pi (a)$
. The proof will be complete once we show that
$\lambda _{(x_1,x_2)}=\lambda _{(a,x_1)}$
. To this end, since
$\nu $
is a shift-invariant measure, making the change of variables
$z \mapsto z-w$
we get that
$$ \begin{align*}\lambda_{(x_1,x_2)}=\int_Z \eta_{\ell z+\ell w + \pi(a)} \times \eta_{mz + (\ell+m)w+\pi(a)}\ d\nu(z)=\int_Z \eta_{\ell z+\pi(a)} \times \eta_{mz + \ell w + \pi(a)}\ d\nu(z),\end{align*} $$
which equals
$\lambda _{(a,x_1)}$
since
$\pi (x_1)=\ell w + \pi (a)$
.
The last result illuminates why this particular definition of
$\sigma _a$
is useful. The measure was defined so that it essentially only witnesses pairs
$(x_1,x_2)\in X\times X$
whose projection on the Kronecker give rise to
$3$
-term
$(\ell ,m)$
-progressions in Z through
$(\pi (a), \pi (x_1),\pi (x_2))$
. This is apparent from the equalities
$\pi (x_1)-\pi (a)=\ell w$
and
$\pi (x_2)-\pi (x_1)=m w$
, some
$w\in Z$
, which hold for any
$(x_1,x_2)\in P.$
Then, a potential route to finding
$(\ell ,m)$
-Erdős progressions of the form
$(a,x_1,x_2) \in X^3$
is laid out. It is sufficient to find a pair
$(x_1,x_2)\in P$
with
$(x_1,x_2)\in \operatorname {supp}{\lambda _{(x_1,x_2)}}$
, and such that
$(a,x_1)$
is
$(T^{\ell }\times T^m)$
-generic for
$\lambda _{(a,x_1)}$
, which coincides with
$\lambda _{(x_1,x_2)}$
. To this end, we shall also need two relations between the measure
$\mu $
and push-forwards of projections of
$\sigma _a$
.
Lemma 3.7. Let
$\pi _i: X\times X \to X$
denote the projection
$(x_1,x_2) \mapsto x_i$
onto the i-th coordinate, where
$i\in \{1,2\}$
. Then, if
$\pi _i \sigma _a$
denotes the push-forward of
$\sigma _a$
by
$\pi _i$
, we have that
$\frac {1}{\ell }\left ( \pi _1 \sigma _a + T\pi _1 \sigma _a +\dots +T^{\ell -1}\pi _1 \sigma _a \right ) = \mu $
and
$\frac {1}{\ell +m}\left ( \pi _2 \sigma _a + T\pi _2 \sigma _a +\dots + T^{\ell +m-1}\pi _2 \sigma _a \right ) = \mu $
.
Proof. We only prove the first claim as the second one follows similarly. Let
$\ell Z$
denote the subgroup
$\{\ell z = z+z+\cdots +z\ \text {with} \ell \text {summands} \colon z\in Z \}$
and let
$\xi $
denote its Haar measure. Ergodicity of R means that
$\{R^n 0: n\in {\mathbb N}\}$
is dense in Z, and thus
$Z=(\ell Z) \cup (R (\ell Z)) \cup \dots \cup (R^{\ell -1}(\ell Z))$
. Therefore, there exists
$w\in Z$
and
$j\in \{0,1,\dots ,\ell -1\}$
such that
$\pi (a)=R^j(\ell w)=\ell w + jb$
, so that
$$ \begin{align*}\pi_1 \sigma_a= \int_Z \eta_{\ell z+\pi(a)}\ d\nu(z)= \int_Z \eta_{\ell (z+w)+jb}\ d\nu(z)=\int_Z \eta_{\ell z+jb}\ d\nu(z)=\int_{\ell Z+jb} \eta_{u}\ d(R^j \xi)(u).\end{align*} $$
Finally,
$T^i \eta _u=\eta _{R^i u}$
and
$R^{\ell }\xi = \xi $
, which implies that
$$ \begin{align*}\frac{1}{\ell} T^{i}\pi_1 \sigma_a = \int_{\ell Z+jb} T^i \eta_{u}\ d\frac{1}{\ell}(R^j \xi)(u)=\int_{\ell Z+(j+i) b} \eta_{u}\ d\frac{1}{\ell}(R^{j+i} \xi)(u),\end{align*} $$
for each
$i\in \{0,1,\ldots ,\ell -1\}$
, where
$j+i$
is taken mod
$\ell $
and thus
$$ \begin{align*}\frac{1}{\ell}\left( \pi_1 \sigma_a + T\pi_1 \sigma_a +\dots +T^{\ell-1}\pi_1 \sigma_a \right)= \int_{Z} \eta_{z}\ d\frac{1}{\ell}(\xi+R\xi+\dots + R^{\ell-1}\xi)(z)=\mu.\\[-42pt]\end{align*} $$
3.4 Support of the measure on
$(\ell ,m)-$
Erdős progressions
We begin with some notational remarks. Recall our setting: we have an ergodic system
$(X,\mu ,T)$
with a continuous factor map
$\pi $
to its Kronecker
$(Z,\nu ,R)$
, say R is the rotation by some
$b\in Z$
, and a generic point
$a\in \textbf {gen}(\mu ,T,\Phi )$
for some Følner sequence
$\Phi $
. We write
$z \to \eta _z$
for the disintegretion of
$\mu $
over
$\pi $
. Then if
$k\in {\mathbb N}$
is any, we can define
$X_i=\pi ^{-1}(R^i(k Z))$
, for
$i=0,1,\dots ,k-1$
and consider the ergodic components of
$\mu $
for the transformation
$T^{k}$
given by
$$ \begin{align} \mu_i=\int_Z \eta_{k z+ib}\ d\nu(z)=\int_{k Z+ib} \eta_u\ d(R^i \zeta)(u), \end{align} $$
where
$\zeta $
is the Haar measure on
$k Z$
. This subsection is devoted to showing that if
$$ \begin{align} S=\{(x_1,x_2) \in X \times X: (x_1,x_2) \in \operatorname{supp}(\lambda_{(x_1,x_2)})\}, \end{align} $$
then
$\sigma _a(S)=1$
. We begin with an extension of Proposition
$3.10$
of [Reference Kra, Moreira, Richter and Robertson15].
Remark 3.8. In the above setting, for any
$x\in X_i$
we have that
$\pi (x)=k w+ib$
, some
$w\in Z$
,
$i=0,1,\ldots ,k-1$
.
For the next result we use notation from [Reference Kra, Moreira, Richter and Robertson15]. In particular,
$\mathcal {F}(X)$
denotes the family of nonempty and closed subsets of the compact metric space
$(X,d)$
, endowed with the Hausdorff metric, denoted by
$\mathbf {H}$
.
Proposition 3.9. Fix a system
$(X,\mu ,T)$
and a continuous factor map
$\pi $
to its Kronecker factor
$(Z,\nu ,R)$
. Also fix
$k\in {\mathbb N}$
and a disintegration
$z \mapsto \eta _z$
over
$\pi $
. There is a sequence
$\delta (j) \to 0$
, such that for
$\mu $
-almost every
$x\in X$
(with
$\pi (x)=k w+ib$
as in Remark 3.8) the following holds: for every neighbourhood U of x we have
$$ \begin{align} \lim_{j\to \infty} \frac{\nu \left(\{z \in Z: \eta_{k z + ib} (U)> 0 \} \cap B(w, \delta(j))\right)}{\nu (B(w, \delta(j)))}=1. \end{align} $$
Remark. This result almost follows directly from [Reference Kra, Moreira, Richter and Robertson15, Proposition 3.10] by considering the finitely many ergodic components of
$(X,\mu ,T^k)$
. Some additional information provided here is the fact that the sequence
$(\delta (j))_{j\in {\mathbb N}}$
does not depend on the choice of the ergodic component.
Proof. We consider the maps
$\Phi _{i}: Z \to {\mathcal F}(X)$
defined by
$\Phi _{i}(z)=\operatorname {supp}(\eta _{k z+ib})$
, for any
$z\in Z$
and
$i \in \{0,1,2,\ldots ,k-1\}$
. These maps are Borel measurable as the composition of three Borel measurable maps,
$z \mapsto \ell z +ib$
,
$z\mapsto \eta _z$
and
$\nu \mapsto \operatorname {supp}(\nu )$
(the latter is measurable by way of Lemma
$3.8$
of [Reference Kra, Moreira, Richter and Robertson15]).
Just like in the proof of Proposition
$3.10$
of [Reference Kra, Moreira, Richter and Robertson15], by Lusin’s theorem, for each
$j\in {\mathbb N}$
there is a closed set
$Z_{i,j} \subset Z$
with
$\nu (Z_{i,j})>1-2^{-j}$
and a
$\delta (i,j)>0$
so that for all
$z_1,z_2 \in Z_{i,j}$
,
$$ \begin{align*}d(z_1,z_2)\leq \delta(i,j) \implies \mathbf{H}(\Phi_i(z_1) , \Phi_i(z_2))< \frac{1}{j}.\end{align*} $$
If we consider the sets
$$ \begin{align*}K_{i,j}=\{ z\in Z_{i,j} \colon \nu\left(B(z,\delta(i,j)) \cap Z_{i,j} \right)> \left( 1-\frac{1}{j} \right)\nu\left( B(z,\delta(i,j) \right) \}\end{align*} $$
and let
$K_{i}=\bigcup _{M\geq 1} \bigcap _{j\geq M} K_{i,j}$
it follows by the same argument as in the proof of Proposition
$3.10$
in [Reference Kra, Moreira, Richter and Robertson15] that
$\nu (K_{i})=1$
.
Next, we let
$L^{\prime }_{i}=\{x\in X: x\in \operatorname {supp}(\eta _{\pi (x)}) \} \cap \pi ^{-1}(k K_{i}+ib)$
. By the above we see that
$\nu (k K_{i})=\nu (k Z)$
and since
$\mu (\{x\in X: x\in \operatorname {supp}(\eta _{\pi (x)}) \})=1$
(see Lemma
$3.9$
in [Reference Kra, Moreira, Richter and Robertson15]) it follows that
$\mu _i(L^{\prime }_i)=1$
. Thus, setting
$L'=L^{\prime }_0 \cup L^{\prime }_1 \cup \dots \cup L^{\prime }_{k-1}$
we have
$\mu (L')=1$
.
Fix
$x\in L'$
, and
$i\in \{0,1,\ldots ,k-1\}$
so that
$x\in L^{\prime }_i$
and let U be an open neighbourhood of x. In this case
$\pi (x)=k w+ib$
, some
$w\in K_i$
, because
$\pi (x) \in k K_i+ib$
. Now, as
$w\in K_i$
and U is open there is
$j_0 \in {\mathbb N}$
such that
$w\in K_{i,j}$
and
$B(x,1/j) \subset U$
, for all
$j\geq j_0$
. We claim that
$$ \begin{align} B(w,\delta(i,j)) \cap Z_{i,j} \subset H:= \{z\in Z: \eta_{kz+ib}(U)>0\}. \end{align} $$
Indeed, let
$w' \in B(w,\delta (i,j)) \cap Z_{i,j}$
. As
$d(w',w)<\delta (i,j)$
and
$w',w$
are continuity points for
$\Phi _i$
, we see that
$\mathbf {H}(\Phi _i(w),\Phi _i(w'))<1/j.$
Then, because
$x\in \Phi _i(w)$
, there exists
$x'\in \Phi _i(w')$
with
$d(x,x')<1/j$
. This of course implies that
$x' \in U$
and so
$x'\in U \cap \Phi _i(w')$
. As
$\Phi _i(w')=\operatorname {supp}(\eta _{kw'+ib})$
it follows that
$\eta _{kw'+ib}(U)>0$
, that is
$w' \in H$
. As
$w\in K_{i,j}$
it follows from (3.14) and by the construction of
$Z_{i,j}$
that
$$ \begin{align*}\frac{\nu(H\cap B(w,\delta(i,j))}{\nu(B(w,\delta(i,j))} \geq 1-\frac{1}{j},\end{align*} $$
for all
$j\geq j_0$
. This then implies that
$$ \begin{align*}\lim_{j\to \infty} \frac{\nu(H\cap B(w,\delta(i,j))}{\nu(B(w,\delta(i,j))} = 1.\end{align*} $$
Setting
$\delta (j)=\min _{\{i=0,1,\ldots ,k-1\}} \delta (i,j)$
, for each
$j\in {\mathbb N}$
, gives (3.13).
We are now in the position to prove the main result of this section.
Proposition 3.10. Let
$S=\{(x_1,x_2) \in X \times X: (x_1,x_2) \in \operatorname {supp} (\lambda _{(x_1,x_2)})\}$
as in (3.12). Then
$\sigma _a(S)=1.$
Proof. Using Proposition 3.9 above for
$k=\ell $
and
$k= m$
, we find a sequence
$\delta (j) \to 0$
and two sets
$L,L' \subset X$
such that each point
$x'\in L'$
satisfies (3.13) with
$k=\ell $
and each
$x\in L$
satisfies (3.13) with
$k=m$
. Now,
$\mu (L)=\mu (L')=1$
and using Lemma 3.7 we see that
$\sigma _a(L' \times L)=1$
. To see this simply note that
$L' \times L=(L' \times X) \cap (X \times L)$
and
$\pi _1\sigma _a(L')=\pi _2\sigma _a(L)=1$
. We have thus reduced matters to showing that
$L' \times L \subset S$
.
To this end, let
$(x_0,x_1) \in L' \times L$
and
$U_0, U_1$
be neighbourhoods of
$x_0, x_1$
respectively. It suffices to verify that
$\lambda _{(x_0,x_1)}(U)>0,$
where
$U=U_0 \times U_1$
. Writing
$\pi (x_0)=\ell w_0+i_0b$
and
$\pi (x_1)=mw_1+i_1b$
as in Remark 3.8, we have that
$$ \begin{align*} \lambda_{(x_0,x_1)} &= \int_Z \eta_{\ell z+\ell w_0+i_0b} \times \eta_{mz + mw_1+i_1b } \mathop{}\!\mathrm{d} \nu(z) \end{align*} $$
and making the change of variables
$z \mapsto z-w_0$
we see that
$$ \begin{align*} \lambda_{(x_0,x_1)}(U) &= \int_Z \eta_{\ell z+i_0b}(U_0) \times \eta_{mz + m(w_1-w_0)+i_1b }(U_1) \mathop{}\!\mathrm{d} \nu(z). \end{align*} $$
Now, as
$x_0 \in L'$
and
$x_1 \in L$
, there is
$\delta>0$
such that
$$ \begin{align} \frac{\nu \left(\{z \in Z: \eta_{\ell z+i_0b} (U_0)> 0 \} \cap B(w_0, \delta)\right)}{\nu (B(w_0, \delta))}\geq \frac{5}{6} \end{align} $$
and also
$$ \begin{align*} \frac{\nu \left(\{z \in Z: \eta_{mz+i_1b} (U_1)> 0 \} \cap B(w_1, \delta)\right)}{\nu (B(w_1, \delta))}\geq \frac{5}{6}. \end{align*} $$
But
$\{z \in Z: \eta _{mz+i_1b} (U_1)> 0 \} - (w_1-w_0) = \{z \in Z: \eta _{mz+m(w_1-w_0)+i_1b} (U_1) > 0 \}$
and so we get
$$ \begin{align} \frac{\nu \left(\{z \in Z: \eta_{mz+m(w_1-w_0)+i_1b} (U_1)> 0 \} \cap B(w_0, \delta)\right)}{\nu (B(w_0, \delta))}\geq \frac{5}{6}. \end{align} $$
Finally, we consider the set G defined by
$$ \begin{align*}W=\{z\in Z: \eta_{\ell z+i_0b}(U_0)>0\ \text{and}\ \eta_{mz+m(w_1-w_0)+i_1b}(U_1)>0 \}.\end{align*} $$
It is clear from (3.15) and (3.16) that W contains at least half of the ball
$B(w_0,\delta )$
and thus
$\nu (W)>0.$
As for all
$z \in W$
we have
$$ \begin{align*} \eta_{\ell z+ i_0b} \times \eta_{mz + m(w_1-w_0)+ i_1b} (U_0 \times U_1)>0 \end{align*} $$
and
$\nu (W)>0$
, it follows that
$\lambda _{(x_0,x_1)}(U_0\times U_1)>0$
, as desired.
3.5 Proofs of correspondence principles
We move on to prove the correspondence principle-type of results stated in Lemmas 2.8 and 2.9. We start with the latter as it has a slightly simpler proof.
Recall that
$\Sigma $
denotes the space
$\{0,1\}^{{\mathbb Z}}$
and is endowed with the product topology so that it is compact metrizable. We also let
$S \colon \Sigma \to \Sigma $
denote the shift transformation given by
$S(x(n))=x(n+1)$
, for any
$n\in {\mathbb Z}$
,
$x=(x(n))_{n\in {\mathbb Z}} \in \Sigma $
. We also recall the statements for convenience.
Lemma 2.9. Let
$A\subset {\mathbb N}$
and
$\ell ,m\in {\mathbb N}$
with
$k=m/\ell $
. Then, there exists an ergodic system
$(\Sigma \times \Sigma , \mu , S \times S)$
, an open set
$E\subset \Sigma $
, a pair of points
$a",a\in \Sigma $
and a Følner sequence
$\Phi $
, such that
$(a",a)\in \mathbf {gen}(\mu ,\Phi )$
and
$$ \begin{align*} (\ell+m)\mu(\Sigma \times E) + \ell \mu(E \times \Sigma) \geq (2\ell+m)\left( (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A) - k \right). \end{align*} $$
It also holds that
$A = \{ n \in {\mathbb N}: S^n a \in E \}$
and
$A/(\ell +m ) =\{n\in {\mathbb N}: S^{\ell n}a" \in E\}$
.
Proof. Let
$A \subset {\mathbb N}$
. By definition, there exists a sequence
$(N_i)$
of positive integers such that
$$ \begin{align*}\overline{\mathop{}\!\mathrm{d}}(A)=\lim_{i\to \infty} \frac{\left|A \cap [1,N_i]\right|}{N_i}.\end{align*} $$
We let
$a\in \Sigma = \{0,1\}^{{\mathbb Z}}$
be the indicator of A, that is,
$$ \begin{align*} a(n) = \left\{ \begin{array}{cc} 1 & \text{if } n\in A \\ 0 & \text{otherwise}. \end{array} \right. \end{align*} $$
Moreover, we let
$a"\in \Sigma $
be defined by
$$ \begin{align*} a"(n) = \left\{ \begin{array}{cc} a((\ell+m )i) & \text{if } n=\ell i,\text{ some } i\in {\mathbb N} \\ 1 & \text{otherwise}. \end{array} \right. \end{align*} $$
If
$E=\{x\in \Sigma \colon x(0)=1\}$
, we observe that E is clopen in
$\Sigma $
,
$A=\{n\in {\mathbb N}\colon S^na \in E\}$
and also
$$ \begin{align*}\{n\in {\mathbb N}: S^{\ell n}a" \in E\} = \{n\in {\mathbb N}: S^{(\ell+m )n}a\in E\}= A/(\ell+m ).\end{align*} $$
Now let
$N^{\prime }_i=\lfloor N_i/(k+1)\rfloor $
, for all
$i\in {\mathbb N}$
,
$i\geq k+1$
, and consider the sequence of Borel probability measures
$(\mu _i)$
on
$\Sigma \times \Sigma $
given by
$$ \begin{align*}\mu_i=\frac{1}{N^{\prime}_i} \sum_{n=1}^{N^{\prime}_i} \delta_{(S \times S)^n(a",a)}.\end{align*} $$
Letting
$\mu '$
be a weak* accumulation point of
$(\mu _i)$
we obtain an
$(S\times S)$
-invariant measure. It follows by definition that for all
$i\in {\mathbb N}$
,
$i\geq k+1$
, we have
$$ \begin{align} \mu_i(\Sigma \times E)=\frac{1}{N^{\prime}_i} \sum_{n=1}^{N^{\prime}_i} \delta_{S^na}(E) = \frac{\left| A\cap [1, N^{\prime}_i ] \right| }{N^{\prime}_i}. \end{align} $$
For any such i we also have that
$$ \begin{align} \mu_i(\Sigma \times E)&=\frac{1}{N^{\prime}_i} \sum_{n=1}^{N^{\prime}_i} \delta_{S^na}(E) = \frac{1}{N^{\prime}_i} \left( \sum_{n=1}^{N_i} \delta_{S^na}(E) - \sum_{n=N^{\prime}_i+1}^{N_i} \delta_{S^na}(E) \right) \nonumber \\[5pt] & \geq \frac{k+1}{N_i} \left( \sum_{n=1}^{N_i} \delta_{S^na}(E)- \frac{k}{k+1}N_i+o_{N_i\to \infty}(N_i) \right)= (k+1) \frac{\left|A \cap [ 1, N_i ] \right|}{N_i}-k+o_{N_i\to \infty}(1) \end{align} $$
Taking limits in (3.18) as
$i\to \infty $
we have, by the definition of
$\mu '$
, the fact that
$E\subset X$
is clopen and the choice of
$(N_i)$
that
$$ \begin{align} \mu'(\Sigma \times E) \geq (k+1) \cdot \overline{\mathop{}\!\mathrm{d}}(A)-k. \end{align} $$
On the other hand, for any
$i\in {\mathbb N}$
,
$i\geq k+1$
, we have that
$$ \begin{align} \mu_i(E \times \Sigma )&=\frac{1}{N^{\prime}_i} \sum_{n=1}^{N^{\prime}_i} \delta_{S^{n}a"}(E) = \frac{1}{N^{\prime}_i} \left( \sum_{n=1,n\notin \ell {\mathbb N}}^{N_i'} \delta_{S^{n}a"}(E) + \sum_{n=1}^{\lfloor N^{\prime}_i/\ell \rfloor }\delta_{S^{\ell n}a"}(E) \right) \nonumber \\[5pt] &= \frac{1}{N_i'} \left( N_i'-\lfloor \frac{N_i'}{\ell}\rfloor+ \sum_{n=1}^{\lfloor N^{\prime}_i/\ell \rfloor }\delta_{S^{(\ell+m ) n}a}(E) \right) \geq 1-\frac{1}{\ell}+ \frac{1}{N_i'} \sum_{n=1}^{\lfloor N_i/(\ell+m) \rfloor -2}\delta_{S^{(\ell+m ) n}a}(E) \nonumber \\[5pt] & = 1-\frac{1}{\ell} + (k+1)\frac{|A\cap (\ell+m ){\mathbb N} \cap [1,N_i]|}{N_i} + o_{N_i\to \infty}(1) , \end{align} $$
where in the inequality we used that
$\ell +m=\ell (k+1)$
. Now, observe that
$$ \begin{align*}|A\cap (\ell+m ){\mathbb N} \cap [1,N_i]| = |A\cap [1,N_i]| - |A\cap \left( {\mathbb N}\setminus (\ell+m ){\mathbb N} \right) \cap [1,N_i]| \geq |A\cap [1,N_i]|-N_i+\frac{N_i}{(\ell+m )},\end{align*} $$
so that
$$ \begin{align*}\liminf_{i\to \infty} \frac{|A\cap (\ell+m ){\mathbb N} \cap [1,N_i]|}{N_i} \geq \overline{\mathop{}\!\mathrm{d}}(A)-1+\frac{1}{(\ell+m )}.\end{align*} $$
Using this and taking limits as
$i\to \infty $
in (3.20) we see that
$$ \begin{align} \mu'(E \times \Sigma ) \geq 1-\frac{1}{\ell}+(k+1)\left(\overline{\mathop{}\!\mathrm{d}}(A)-1+\frac{1}{\ell+m }\right)=(k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A)-k. \end{align} $$
Combining (3.19) and (3.21) we have that
$$ \begin{align*}(\ell+m)\mu'(\Sigma \times E) + \ell \mu'(E \times \Sigma ) \geq (2\ell+m)\left( (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A) - k \right).\end{align*} $$
Although
$\mu '$
is not necessarily ergodic, we can use its ergodic decomposition to find an
$(S \times S)$
-ergodic component of it, call it
$\mu $
, such that
$$ \begin{align*}(\ell+m)\mu(\Sigma \times E) + \ell \mu(E \times \Sigma ) \geq (2\ell+m)\left( (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A) - k \right).\end{align*} $$
Without loss of generality we may assume that
$\mu $
is supported on the orbit closure of
$(a",a)$
, since this holds for
$\mu '$
by construction. Then by a standard argument (see [Reference Furstenberg6, Proposition 3.9]) we see there is a Følner sequence
$\Phi $
in
${\mathbb N}$
, such that
$(a",a) \in \textbf {gen}(\mu ,\Phi )$
. This completes the proof.
Lemma 2.8. Let
$A\subset {\mathbb N}$
and
$\ell ,m \in {\mathbb N}$
with
$k=m/\ell $
and let
$q=\lceil k \rceil $
, the ceiling of k. Then, there exist an ergodic system
$(\Sigma \times \Sigma , \mu , S^{(q+1)} \times S)$
, an open set
$E\subset \Sigma $
, a pair of points
$a,a'\in \Sigma $
and a Følner sequence
$\Phi $
, such that
$(a',a)\in \textbf {gen}(\mu ,\Phi )$
and
$$ \begin{align*} (\ell+m)\mu(\Sigma \times E) + \ell \sum_{j=0}^{q} \mu(S^{-j}E \times \Sigma) \geq (\ell+m) \left((k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A)-k \right)+\ell (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A)+\ell(q-k). \end{align*} $$
It also holds that
$A=\{n\in {\mathbb N}: S^n a \in E \}$
and
$(A-j)/(\ell +m ) =\{n\in {\mathbb N}: S^{(q+1)\ell n+j}a' \in E\}$
, for each
$j=0,1,\dots ,\ell +m -1$
, where
$(A-j)/(\ell +m )=\{n\in {\mathbb N}: n(\ell +m )+j\in A\}$
.
Proof. Let
$A \subset {\mathbb N}$
. As before, let
$(N_i)$
be a sequence of integers such that
$$ \begin{align*}\overline{\mathop{}\!\mathrm{d}}(A)=\lim_{i\to \infty} \frac{\left|A \cap [1,N_i]\right|}{N_i}\end{align*} $$
and
$a\in \Sigma = \{0,1\}^{{\mathbb Z}}$
be the indicator of A. This time we let
$a'\in \Sigma $
be defined by
$$ \begin{align*} a'(n) = \left\{ \begin{array}{cc} a(\ell(k+1)i+j) & \text{if } n=\ell(q+1)i+j, \text{ some } i\in {\mathbb N}, j\in \{0,1,\dots,\ell(k+1)-1\} \\ 1 & \text{otherwise}. \end{array} \right. \end{align*} $$
Observe that
$a'$
is well-defined because
$\ell (k+1) \leq \ell (q+1)$
. If
$E=\{x\in \Sigma \colon x(0)=1\}$
, we observe that E is clopen in
$\Sigma $
,
$A=\{n\in {\mathbb N}\colon S^na \in E\}$
and, since
$(\ell +m )n=\ell (k+1)n$
,
$$ \begin{align*}\{n\in {\mathbb N}: S^{(q+1)\ell n+j}a' \in E\} = \{n\in {\mathbb N}: S^{(\ell+m )n+j}a\}= (A-j)/(\ell+m ),\end{align*} $$
for each
$j\in \{0,1,\dots ,\ell +m -1\}$
. Now let
$N^{\prime }_i=\lfloor N_i/(k+1)\rfloor $
, for all
$i\in {\mathbb N}$
and consider the sequence of Borel probability measures
$(\mu _i)$
on
$\Sigma \times \Sigma $
given by
$$ \begin{align*}\mu_i=\frac{1}{N^{\prime}_i} \sum_{n=1}^{N^{\prime}_i} \delta_{(S^{(q+1)} \times S)^n(a',a)},\end{align*} $$
if
$i\geq k+1$
, and let
$\mu '$
be a weak* accumulation point of
$(\mu _i)$
. As before we have that
$$ \begin{align} \ \mu'(\Sigma \times E) \geq (k+1) \cdot \overline{\mathop{}\!\mathrm{d}}(A)-k, \end{align} $$
On the other hand, for any
$i\in {\mathbb N}$
,
$i\geq k+1$
, we have that
$$ \begin{align} \sum_{j=0}^{q} \mu_i(S^{-j}E \times \Sigma) = \frac{1}{N^{\prime}_i} \sum_{j=0}^{q} \sum_{n=1}^{N^{\prime}_i} \delta_{S^{(q+1)n}a'}(S^{-j}E) = \frac{k+1}{N_i} \left( \sum_{n=1}^{N_i'(q+1)} \delta_{S^{n}a'}(E)\right) +o_{N_i\to \infty}(1). \end{align} $$
We can relate this with the density of A because
$$ \begin{align*} \sum_{n=1}^{N_i'(q+1)} \delta_{S^{n}a'}(E) & = \sum_{n=1}^{\lfloor N_i/(\ell(k+1)) \rfloor} \sum_{j=0}^{\ell(k+1)-1} \delta_{S^{\ell(q+1)n+j}a'}(E) + \sum_{n=1}^{\lfloor N_i/(\ell(k+1)) \rfloor} \sum_{j=\ell(k+1)}^{\ell(q+1)-1} 1 + o_{N_i\to \infty}(N_i) \\ & = \sum_{n=1}^{\lfloor N_i/(\ell(k+1)) \rfloor} \sum_{j=0}^{\ell+m -1} \delta_{S^{(\ell+m )n+j}a}(E) + \frac{N_i}{\ell(k+1)}\left( \ell(q+1)-\ell(k+1) \right) + o_{N_i\to \infty}(N_i) \\ & = \sum_{n=1}^{N_i} \delta_{S^n a} +N_i\frac{q-k}{k+1} + o_{N_i\to \infty}(N_i)\\ & = |A \cap [1, N_i ]| + N_i\frac{q-k}{k+1} + o_{N_i\to \infty}(N_i), \end{align*} $$
where we have used, when convenient, the equality
$\ell +m =\ell (k+1)$
and the fact that
$q=\lceil k \rceil \geq k$
. Using this in (3.23) and taking limits as
$i\to \infty $
we see that
$$ \begin{align} \sum_{j=0}^{q} \mu'(S^{-j}E \times \Sigma) \geq (k+1) \cdot \overline{\mathop{}\!\mathrm{d}}(A)+ q-k. \end{align} $$
It follows by combining (3.22) and (3.24) that
$$ \begin{align*}(\ell+m)\mu'(\Sigma \times E) + \ell \sum_{j=0}^{q} \mu'(S^{-j}E \times \Sigma) \geq (\ell+m) \left((k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A)-k \right)+\ell (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A)+\ell(q-k).\end{align*} $$
The rest of the proof follows the same arguments as the previous one.
4 Proofs of main dynamical theorems
For the proof of our main result we need a lemma that guarantees
$(T^{\ell } \times T^m)$
-generic points, for almost all the measures
$\lambda _{(a,x_1)}$
with prescribed first coordinate.
Lemma 4.1. If
$(X,\mu ,T)$
is an ergodic system and
$a\in \textbf {gen}(\mu ,\Phi )$
for some Følner sequence
$\Phi $
, then for
$\mu $
-almost every
$x_1 \in X$
we have that
$(a,x_1)$
is
$(T^{\ell } \times T^m)$
-generic for
$\lambda _{(a,x_1)}$
.
Proof. The proof is an adaptation of the proof of Lemma
$3.12$
of [Reference Kra, Moreira, Richter and Robertson15], but requires a few adjustments which are not immediately obvious.
Using property
$(iii)$
of Proposition 3.4 and Fubini’s theorem it follows that for each one of a full measure set of points
$x'\in \operatorname {supp}(\mu )$
there is a full measure set of points
$x'\in X$
so that
$(x',x) \in \textbf {gen}(\lambda _{(x',x)},T^{\ell }\times T^m, \Phi ')$
, where
$\Phi '=(\{1,\dots ,N\})_{N\in {\mathbb N}}$
. We let
$(G_j)_{j=1}^{\infty }$
be a dense subset of
$C(X \times X)$
and for each
$j\in {\mathbb N}$
we set
$\tilde {G}_j(x,y)=\int _{X\times X} G_j \ d\lambda _{(x,y)}$
. As the map
$(x_1,x_2) \mapsto \lambda _{(x_1,x_2)}$
is continuous and
$(T^{\ell } \times T^m)$
-invariant, it follows that each
$\tilde {G}_j$
is continuous and
$(T^{\ell } \times T^m)$
-invariant.
Now, as
$a\in \textbf {gen}(\mu ,T,\Phi )$
we have that
$\operatorname {supp}(\mu ) \subset \overline {O_T(a)} \subset \bigcup _{j=0}^{\ell -1} \overline {O_{T^{\ell }}(T^{j}a)}$
, where
$O_S(a)$
is the (forward) orbit of a under a homeomorphism
$S: X\to X$
, that is,
$\{S^n a \colon n\in {\mathbb N} \}$
. Therefore,
$\mu (\overline {O_{T^{\ell }}(a)})>0$
and so we can choose some
$x'$
as above with
$x'\in \overline {O_{T^{\ell }}(a)}$
. This allows us to find, for each
$k\in {\mathbb N}$
and
$N(k)\in {\mathbb N}$
, an
$s(k)\in {\mathbb N}$
such that 
and 
for all
$j\leq k$
.
Because
$(x',x)$
is
$(T^{\ell } \times T^m)$
-generic for
$\lambda _{(x',x)}$
for
$\mu $
-almost every
$x\in X$
, we can find for each
$k\in {\mathbb N}$
some
$N(k)\in {\mathbb N}$
such that
$$ \begin{align*}F_k(x)= \max_{1\leq j\leq k} \left| \frac{1}{N(k)} \sum_{n=1}^{N(k)} G_j(T^{\ell n} x', T^{m n} x) - \tilde{G_j}( x', x) \right|\end{align*} $$
satisfies 
By the choice of
$s(k)$
we have that
$$ \begin{align*}\tilde{F_k}(x):= \max_{1\leq j\leq k} \left| \frac{1}{N(k)} \sum_{n=1}^{N(k)} G_j(T^{\ell (n+s(k))} a, T^{m n} x) - \tilde{G_j}( T^{\ell s(k)}a, x) \right|\end{align*} $$
satisfies 
. Then, by the
$(T^{\ell } \times T^m)$
-invariance of
$\tilde {G}_j$
, we can consider
$\Psi _k=\{s(k)+1,\dots ,s(k)+N(k)\}$
and then we see that
$$ \begin{align*}F^{\prime}_k(x):=\tilde{F_k}(T^{m s(k)} x)= \max_{1\leq j\leq k} \left| \frac{1}{|\Psi_k|} \sum_{n\in \Psi_k} G_j(T^{\ell n} a, T^{m n} x) - \tilde{G_j}( a, x) \right|.\end{align*} $$
As
$\mu $
is
$T-$
invariant it follows that 
and so, if we define
$F(x):=\sum _{k=1}^{\infty } F^{\prime }_k(x)$
it follows that 
and so F is finite
$\mu $
-almost everywhere. Finally, for each
$x_1\in X$
such that
$F(x_1)<\infty $
it must hold that
$F^{\prime }_k(x_1) \xrightarrow {} 0$
as
$k\to \infty $
and so
$(a,x_1) \in \textbf {gen}(\lambda _{(a,x_1)},T^{\ell }\times T^m, \Psi )$
.
Combining some of the above results we can guarantee the existence of
$(\ell ,m)$
-Erdős progressions via the following analogue of Proposition
$3.3$
in [Reference Kousek and Radić12]. The proof is almost identical to that of the latter mentioned proposition and so we omit it. For reference, the established properties of the measures
$\sigma _a$
and
$\lambda _{(x_1,x_2)}$
used in the proof are those in Lemma 4.1, Lemma 3.7 and Proposition 3.10.
Proposition 4.2. Let
$(X,\mu ,T)$
be an ergodic system and assume there is a continuous factor map
$\pi \colon X \to Z$
to its Kronecker factor. Let
$a\in \textbf {gen}(\mu ,\Phi )$
, for some Følner sequence
$\Phi $
. Then for
$\sigma _a$
-almost every
$(x_1,x_2) \in X \times X$
, the point
$(a,x_1,x_2)$
is an
$(\ell ,m)$
-Erdős progression.
We are now in the position to prove all our main dynamical results. Before presenting the proofs, we emphasise again that, according to our discussion in the beginning of Section 3.2, these theorems also imply Theorems 2.2, 2.6 and 2.7, respectively.
Proof of Theorem 3.1.
Since for
$\sigma _a$
-almost every point
$(x_1,x_2)\in X\times X$
the triple
$(a,x_1,x_2)$
is an
$(\ell ,m)$
-Erdős progression by Proposition 4.2, we simply need to show that
$\sigma _a(X \times T^{-t}E)>0$
for some
$t\in {\mathbb N}.$
The latter follows directly by the fact that
$\pi _2 \sigma _a \left ( \bigcup _{t\in {\mathbb N}} T^{-t}E \right )>0$
. Indeed, as
$\mu $
is ergodic we have that
$\mu (\bigcup _{t\in {\mathbb N}}T^{-t}E)= 1$
and thus, by way of Lemma 3.7, we actually see that
$\pi _2 \sigma _a \left ( \bigcup _{t\in {\mathbb N}} T^{-t}E \right ) = 1$
.
Remark 4.3. In fact one can modify the above proof to show that there exist
$t_1,t_2\in {\mathbb N}$
such that
$\sigma _a(E\times T^{-t_1}E)>0$
and
$\sigma _a(T^{-t_2}E \times T^{-t_2}E)>0.$
These in turn guarantee
$(\ell ,m)$
-Erdős progressions
$(a,x_1,x_2), (a,x_1',x_2')\in X^3$
with
$(x_1,T^{t_1}x_2),(T^{t_2}x_1',T^{t_2}x_2') \in E\times E$
and then, Theorem 1.2 can be strengthened, so that for any set
$A\subset {\mathbb N}$
with
$\mathop {}\!\mathrm {d}^{*}(A)>0$
the following holds:
-
(i) There exist an infinite set
$B\subset {\mathbb N}$
and a shift
$t\in {\mathbb N}$
such that
$\ell B \subset A$
and
$$ \begin{align*}\{mb_1 + \ell b_2\colon b_1,b_2\in B,\ b_1 < b_2\} +t \subset A.\end{align*} $$
-
(ii) There exist an infinite set
$B\subset {\mathbb N}$
and a shift
$t\in {\mathbb N}$
such that
$$ \begin{align*}\ell B \cup \{mb_1 + \ell b_2\colon b_1,b_2\in B,\ b_1 < b_2\} \subset A-t.\end{align*} $$
Proof of Theorem 3.2.
Applying Proposition 4.2 once again, we only have to show that for some
$j\in \{1,\ldots ,\ell +m\}$
,
$\sigma _a(E_j \times F_j)>0$
, because this would imply the existence of
$x_1,x_2 \in X$
so that
$(a,x_1,x_2) \in X^3$
is an
$(\ell ,m)$
-Erdős progression and
$(x_1,x_2) \in E_j \times F_j$
. This would follow from the inequality
$$ \begin{align} \sigma_a(E_j\times X)+ \sigma_a(X\times F_j)>1, \end{align} $$
because
$$ \begin{align*}E_j \times F_j=\left(E_j\times X\right) \cap \left(X\times F_j\right)\end{align*} $$
and
$\sigma _a$
is a probability measure. It suffices to show that (4.1) has to be satisfied with
$j=1$
provided that it fails for
$j=2,\ldots ,\ell +m$
. In particular, we assume that
$$ \begin{align*}\sum_{j=2}^{\ell+m} \left(\sigma_a(E_j\times X)+ \sigma_a(X\times F_j) \right)\leq \ell+m-1,\end{align*} $$
which can be rewritten as
$$ \begin{align} \sum_{j=2}^{\ell+m} \left(\pi_1\sigma_a(E_j)+ \pi_2\sigma_a(F_j) \right)\leq \ell+m-1. \end{align} $$
Under this assumption, we have to show that
$\pi _1\sigma _a(E_1)+\pi _2 \sigma _a(F_1)>1$
, which by Lemma 3.7 can be rewritten as
$$ \begin{align} \pi_1\sigma_a(E_1)+(\ell+m)\mu(F_1)-\sum_{j=1}^{\ell+m-1}T^{j}\pi_2\sigma_a(F_1)>1. \end{align} $$
Recalling that
$F_j=T^{-(j-1)}F_1$
, for each
$j=1,\ldots ,\ell +m$
, we see that (4.3) is equivalent to
$$ \begin{align*} \pi_1\sigma_a(E_1)+(\ell+m)\mu(F_1)-\sum_{j=2}^{\ell+m}\pi_2\sigma_a(F_j)>1, \end{align*} $$
which by (4.2) would follow from
$$ \begin{align} \pi_1\sigma_a(E_1)+(\ell+m)\mu(F_1)+\sum_{j=2}^{\ell+m}\pi_1\sigma_a(E_j)-(\ell+m-1)>1. \end{align} $$
Next, we note that (4.4) can be rewritten as
$$ \begin{align} (\ell+m)\mu(F_1)+\sum_{j=1}^{\ell+m}\pi_1\sigma_a(E_j)>\ell+m. \end{align} $$
We now recall that
$E_{i+(q+1)}=T^{-1}E_i$
, for
$i=1,\ldots ,\ell +m-q-1$
, and if
$q>m/\ell $
(i.e., whenever
$m/\ell \notin {\mathbb Z}$
) we also consider auxiliary sets
$E_{\ell +m+1},\ldots ,E_{\ell (q+1)}$
such that
$E_{i+(q+1)}=T^{-1}E_i$
, for
$i=1,\ldots ,(\ell -1)(q+1)$
. Then,
$$ \begin{align*}\sum_{j=1}^{\ell(q+1)}\pi_1\sigma_a(E_j)=\sum_{j=1}^{q+1} \sum_{i=0}^{\ell-1} T^{i}\pi_1\sigma_a(E_j)=\ell \sum_{j=1}^{q+1} \mu(E_j)\end{align*} $$
in accordance with Lemma 3.7. We also make the trivial observation that
$$ \begin{align*}\sum_{j=1}^{\ell(q+1)}\pi_1\sigma_a(E_j) -\sum_{j=1}^{\ell+m}\pi_1\sigma_a(E_j) = \sum_{j=\ell(k+1)+1}^{\ell(q+1)} \pi_1\sigma_a(E_j) \leq \ell(q-k),\end{align*} $$
since
$\ell (k+1)=\ell +m$
. Therefore, it follows that
$$ \begin{align*}(\ell+m)\mu(F_1)+\sum_{j=1}^{\ell+m}\pi_1\sigma_a(E_j) \geq (\ell+m)\mu(F_1)+\ell \sum_{j=1}^{q+1}\mu(E_j)-\ell(q-k)\end{align*} $$
Proof of Theorem 3.3.
We need to find an Erdős progression of the form
$(a,x_1,x_2)\in X^3$
with
$(x_1,x_2) \in E \times F$
and as before, by Proposition 4.2 it suffices to show that
$\sigma _a(E \times F)>0$
. Once again, this would follow from
$$ \begin{align*} \sigma_a(E\times X)+ \sigma_a(X\times F)>1. \end{align*} $$
To this end, we simply note that
$$ \begin{align*} \sigma_a(E \times X)+\sigma_a(X \times F)&=\pi_1\sigma_a(E)+\pi_2\sigma_a(F) & \\ &= \ell \mu(E)+(\ell+m)\mu(F)-\sum_{j=1}^{\ell-1}\pi_1\sigma_a(T^{-j}E)- \sum_{i=1}^{\ell+m-1}\pi_2\sigma_a(T^{-i}F) & \quad \\ &\geq \ell\mu(E)+(\ell+m)\mu(F)-(\ell-1)-(\ell+m-1)>1, & \quad \end{align*} $$
where the second equality follows by Lemma 3.7 and the strict inequality by the assumption in (3.3). This concludes the proof.
5 Examples for optimality
In this short section we will show that Theorems 1.7 and 1.8 are optimal. That is, the density thresholds presented in both these results cannot be improved.
Proposition 5.1. Let
$\ell ,m\in {\mathbb N}$
and
$k=m/\ell $
. Then, there exist two sets
$A,A'\subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)=(k+1)/(k+2)=1-1/(k+2)$
and
$\overline {\mathop {}\!\mathrm {d}}(A')=1-1/\left (\ell (k+1)(k+2)\right )$
such that for any infinite set B and any integer
$t\in {\mathbb N}$
we have that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}+t \not \subset A$
and
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\} \not \subset A'.$
Proof of Proposition 5.1.
Let A be the subset of
${\mathbb N}$
defined by
$$ \begin{align*} A = {\mathbb N} \cap \bigcup_{n \in {\mathbb N}} [(k+1)^{2n}, (k+1-1/n) \cdot (k+1)^{2n}). \end{align*} $$
It is clear by the definition of A that
$\overline {\mathop {}\!\mathrm {d}}(A) = \mathop {}\!\mathrm {d}_{\Phi } (A)$
, where
$\Phi =(\Phi _N)$
is the Følner sequence given by
$N \mapsto [1, (k+1-1/N) (k+1)^{2N}) \cap {\mathbb N}$
. We show that
$\overline {\mathop {}\!\mathrm {d}}(A)=(k+1)/(k+2).$
Indeed, first observe that
$\mathop {}\!\mathrm {d}_{\Phi } (A)=\mathop {}\!\mathrm {d}_{\tilde {\Phi }} (\tilde {A})$
, where
$$ \begin{align*} \tilde{A} = {\mathbb N} \cap \bigcup_{n \in {\mathbb N}} [(k+1)^{2n}, (k+1)^{2n+1}) \end{align*} $$
and
$\tilde {\Phi }=(\tilde {\Phi }_N)$
is the sequence given by
$N \mapsto [1, (k+1)^{2N+1}) \cap {\mathbb N}$
and then
$$ \begin{align*} \frac{\left| \tilde{A} \cap [1, (k+1)^{2N+1})] \right|}{ (k+1)^{2N+1}} & = \frac{1}{(k+1)^{2N+1}} \sum_{n=1}^{N} k(k+1)^{2n} \\&= \frac{k}{k+1} \sum_{n=1}^N \frac{1}{((k+1)^{2})^{N-n}} \xrightarrow{N\to \infty} \frac{k}{k+1} \cdot \frac{1}{1-\frac{1}{(k+1)^2}}=\frac{k+1}{k+2}. \end{align*} $$
Now, assume there exist an infinite
$B\subset {\mathbb N}$
and some integer
$t\in {\mathbb N}$
for which
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}+t \subset A$
. In particular, for any
$b'\in B$
fixed there is
$b\in B$
arbitrarily large such that
$\{(\ell +m )b+t,\ell b+mb'+t\}\subset A$
. Then, we can choose b so that,
$(\ell +m )b+t \in [(k+1)^{2(n+1)}, (k+1-\frac {1}{n+1}) (k+1)^{2(n+1)}))$
, for some
$n \in {\mathbb N}$
with respect to which both t and
$b'$
are negligible. Note that
$\ell +m=\ell (k+1)$
and so it follows that
$$ \begin{align*}(k+1)^{2n+1} < \ell b + t < \left(k+1-\frac{1}{n+1}\right) (k+1)^{2n+1} + t.\end{align*} $$
By the choice of b with respect to t and
$b'$
we see that
$mb'+\ell b+t \in [(k+1)^{2n+1},\ (k+1)^{2(n+1)}) \subset {\mathbb N} \setminus A$
, reaching a contradiction. To see why the last claim is true, observe that
$$ \begin{align*}(k+1)^{2(n+1)}-\left(k+1-\frac{1}{n+1}\right) (k+1)^{2n+1} = (k+1)^{2n+1} \cdot \frac{1}{n+1} \xrightarrow{n\to \infty} \infty.\end{align*} $$
This completes the first construction.
Keeping A as defined above we now consider
$A'=A \cup \left ( \bigcup _{j=1}^{\ell +m -1}(\ell +m ){\mathbb N}+j \right )$
. In other words,
$A'=A \cup \left ( \left ({\mathbb N} \setminus A \right ) \setminus \left ( (\ell +m ){\mathbb N} \right ) \right )$
. By the definition of A we have that
${\mathbb N} \setminus A$
is a union of discrete intervals with lower density equal to
$\underline {\mathop {}\!\mathrm {d}}({\mathbb N} \setminus A)=1-\overline {\mathop {}\!\mathrm {d}}(A)=1/(k+2)$
and so
$\underline {\mathop {}\!\mathrm {d}}(\left ({\mathbb N} \setminus A \right ) \cap (\ell +m ) {\mathbb N} )=1/(\ell +m )(k+2)=1/\left (\ell (k+1)(k+2)\right )$
. Since the complement of
$A'$
is precisely
$\left ( {\mathbb N} \setminus A \right ) \cap (\ell +m ){\mathbb N} $
, it follows that
$\overline {\mathop {}\!\mathrm {d}}(A')=1-1/\left (\ell (k+1)(k+2)\right )$
. Finally, we claim there is no infinite set
$B\subset {\mathbb N}$
satisfying
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\} \subset A'$
. Indeed, if there were such a set, we could consider an infinite subset
$B'\subset B$
consisting of integers which are equal modulo
$(\ell +m)$
(see also the proof of Proposition 2.5) and so we would have that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\} \subset A' \cap (\ell +m ){\mathbb N} \subset A$
. This contradicts the first construction and so we conclude.
6 Lower density results
We also want to briefly explore what further results we can get by considering the input of the information provided by a set’s lower asymptotic density. The proofs in this section are straightforward adaptations of the arguments used thus far, so we omit repetitive details, but we include comments regarding all the nonobvious changes in the argumentation.
A possibility to capture this new input – one that has been tried and found to be fruitful in [Reference Kousek and Radić12] – is to replace (3.19), which appears in both correspondence principles in Lemmas 2.8 and 2.9, by the always true inequality
$\mu '(\Sigma \times E) \geq \underline {\mathop {}\!\mathrm {d}}(A).$
To see this recall that
$\mu '$
is defined as a weak* limit of the sequence of measures
$(\mu _i)$
and take the liminf as
$i\to \infty $
in (3.17). Making this simple change in the proofs of the correspondence principles we recover the following results.
Lemma 6.1. Let
$A\subset {\mathbb N}$
and
$\ell ,m \in {\mathbb N}$
with
$k=m/\ell $
and let
$q=\lceil k \rceil $
, the ceiling of k. Then, there exist an ergodic system
$(\Sigma \times \Sigma , \mu , S^{(q+1)} \times S)$
, an open set
$E\subset \Sigma $
, a pair of points
$a,a'\in \Sigma $
and a Følner sequence
$\Phi $
, such that
$(a',a)\in \textbf {gen}(\mu ,\Phi )$
and
$$ \begin{align*} (\ell+m)\mu(\Sigma \times E) + \ell \sum_{j=0}^{q} \mu(S^{-j}E \times \Sigma) \geq (\ell+m)\cdot \underline{\mathop{}\!\mathrm{d}}(A)+\ell(k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A) + \ell(q-k). \end{align*} $$
It also holds that
$A=\{n\in {\mathbb N}: S^n a \in E \}$
and
$(A-j)/(\ell +m ) =\{n\in {\mathbb N}: S^{(q+1)\ell n+j}a' \in E\}$
, for each
$j=0,1,\dots ,\ell +m -1$
, where
$(A-j)/(\ell +m )=\{n\in {\mathbb N}: n(\ell +m )+j\in A\}$
.
Lemma 6.2. Let
$A\subset {\mathbb N}$
and
$\ell ,m\in {\mathbb N}$
with
$k=m/\ell $
. Then, there exists an ergodic system
$(\Sigma \times \Sigma , \mu , S \times S)$
, an open set
$E\subset \Sigma $
, a pair of points
$a",a\in \Sigma $
and a Følner sequence
$\Phi $
, such that
$(a",a)\in \textbf {gen}(\mu ,\Phi )$
and
$$ \begin{align*} (\ell+m)\mu(\Sigma \times E) + \ell \mu(E \times \Sigma) \geq (\ell+m)\cdot \underline{\mathop{}\!\mathrm{d}}(A) +\ell \left( (k+1)\cdot \overline{\mathop{}\!\mathrm{d}}(A)-k \right). \end{align*} $$
It also holds that
$A = \{ n \in {\mathbb N}: S^n a \in E \}$
and
$A/(\ell +m ) =\{n\in {\mathbb N}: S^{\ell n}a" \in E\}$
.
Now that we have these additional correspondence principles we may expand on the arguments presented in Section 2.2, using Theorems 2.6, 2.7 and Proposition 2.3 to get the following combinatorial result.
Theorem 6.3. Let
$A\subset {\mathbb N}$
and
$\ell ,m \in {\mathbb N}$
.
-
1. If
$\underline {\mathop {}\!\mathrm {d}}(A)+\overline {\mathop {}\!\mathrm {d}}(A)>1,$
there is an infinite set
$B\subset {\mathbb N}$
and some
$t\in \{0,1,\ldots ,\ell +m-1\}$
such that
$\{mb_1 + \ell b_2\colon b_1,b_2\in B,\ b_1 \leq b_2\}+t \subset A.$
-
2. If
$\underline {\mathop {}\!\mathrm {d}}(A)+\overline {\mathop {}\!\mathrm {d}}(A)>2-1/(\ell +m),$
there is an infinite set
$B\subset {\mathbb N}$
such that
$\{mb_1 + \ell b_2\colon b_1,b_2\in B, b_1 \leq b_2\} \subset A.$
We have the following immediate corollary of Theorem 6.3.
Corollary 6.4. Let
$A\subset {\mathbb N}$
and
$\ell ,m \in {\mathbb N}$
.
-
1. If
$\underline {\mathop {}\!\mathrm {d}}(A)>1/2,$
there is an infinite set
$B\subset {\mathbb N}$
and some
$t\in \{0,1,\ldots ,\ell +m-1\}$
such that
$\{mb_1 + \ell b_2\colon b_1,b_2\in B,\ b_1 \leq b_2\}+t \subset A.$
-
2. If
$\underline {\mathop {}\!\mathrm {d}}(A)>1-1/(2(\ell +m)),$
there is an infinite set
$B\subset {\mathbb N}$
such that
$\{mb_1 + \ell b_2\colon b_1,b_2\in B, b_1 \leq b_2\} \subset A.$
Remark. Compare this result with the upper density analogues in 1.7 and 1.8. In particular, the threshold values for upper density depend on the parameters m and
$\ell $
involved in the sumsets. It is very surprising that this is no longer the case for threshold values of lower density, at least in the case of shifted sumsets. Of course, some kind of dependence in the case of unshifted patterns is enforced by the fact that infinite sumsets
$mB+\ell B$
essentially ‘live’ in
$(m+\ell ){\mathbb N}$
, as was utilised in the proof of Proposition 2.5.
We will conclude this discussion by proving that Corollary 6.4 (and thus Theorem 6.3 too) is also optimal.
Proposition 6.5. Let
$\ell ,m\in {\mathbb N}$
. There exist two sets
$A,A'\subset {\mathbb N}$
with
$\underline {\mathop {}\!\mathrm {d}}(A)=1/2$
and
$\underline {\mathop {}\!\mathrm {d}}(A')=1-1/(2(\ell +m))$
such that for any infinite set B and any integer
$t\in {\mathbb N}$
we have that
$\{mb_1 + \ell b_2 : b_1, b_2 \in B\ \text {and}\ b_1 \leq b_2\}+t \not \subset A$
and
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\} \not \subset A'.$
Proof of Proposition 6.5.
Let
$k=m/\ell $
and
$A_1,A_2$
be the subsets of
${\mathbb N}$
defined by
$$ \begin{align*} A_1 = {\mathbb N} \cap \bigcup_{n \in {\mathbb N}} [(k+1)^{2n}, (k+1-1/n) \cdot (k+1)^{2n}) \end{align*} $$
and
$$ \begin{align*} A_2 = {\mathbb N} \cap \bigcup_{n \in {\mathbb N}} [ (k+1+1/n) \cdot (k+1)^{2n}, (k+1)^{2(n+1)}). \end{align*} $$
We saw in Proposition 5.1 that there is no infinite set
$B\subset {\mathbb N}$
and integer
$t\in {\mathbb N}$
so that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}+t \subset A_1$
and a symmetrical argument shows the same conclusion holds for
$A_2$
as well.
Next, we observe that the set
$$ \begin{align*}{\mathbb N} \setminus \left( A_1 \cup A_2 \right) = {\mathbb N} \cap \bigcup_{n \in {\mathbb N}} \left[ (k+1-1/n) \cdot (k+1)^{2n}, (k+1+1/n) \cdot (k+1)^{2n} \right]\end{align*} $$
has zero density. This follows from the fact that
$$ \begin{align*}\lim_{N\to \infty} \sum_{n=1}^N \frac{1}{n \cdot (k+1)^{2(N-n)}}= 0,\end{align*} $$
which holds because
$k+1>1$
(for a similar argument see the proof of Proposition
$4.2$
in [Reference Kousek and Radić12]).
We define
$A\subset {\mathbb N}$
by
$$ \begin{align*}A = \left(A_1 \cap 2{\mathbb N} \right) \cup \left( A_2 \cap (2{\mathbb N}+1) \right)\end{align*} $$
and claim that this set satisfies the properties in the statement above. Clearly, by the last argument, we see that
$\mathop {}\!\mathrm {d}(A)=1/2$
and so, in particular,
$\underline {\mathop {}\!\mathrm {d}}(A)=1/2$
. For the second property, assume for contradiction the existence of an infinite set
$B\subset \mathbb{N}$
and some integer
$t\in {\mathbb N}$
so that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}+t \subset A$
. We can pass to an infinite subset
$B'\subset B$
all the elements of which have the same parity. Then, there is
$i\in \{0,1\}$
such that for each
$b_1,b_2 \in B'$
there are
$n_1,n_2\in {\mathbb N}$
for which
$b_1=2n_1+i$
,
$b_2=2n_2+i$
and then
$mb_1+\ell b_2+t=2(mn_1+\ell n_2)+(\ell +m )i+t \in 2{\mathbb N} + (\ell +m )i+t$
. But then, depending on whether
$(\ell +m )i+t$
is even or odd we have that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B'\ \text {and}\ b_1 \leq b_2\}+t$
is contained in
$A\cap 2{\mathbb N}$
or
$A\cap (2{\mathbb N}+1)$
, respectively. In each case we reach a contradiction, because it would have either have to hold that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B'\ \text {and}\ b_1 \leq b_2\}+t \subset A_1$
or
$\{mb_1 + \ell b_2 : b_1,b_2 \in B'\ \text {and}\ b_1 \leq b_2\}+t \subset A_2$
.
For the second part of the construction we keep
$A_1$
and
$A_2$
as they were defined above. Then, we let
$A'\subset {\mathbb N}$
be defined by
$$ \begin{align*}A'= \left(A_1 \setminus (2(\ell+m ){\mathbb N} \right) \cup \left( A_2 \setminus (2(\ell+m ){\mathbb N}+(\ell+m )) \right).\end{align*} $$
We already showed that
$\mathop {}\!\mathrm {d}(A_1 \cup A_2)=1$
and it is easy to see that
$\mathop {}\!\mathrm {d}(A')=1-1/(2(\ell +m ))$
, because we are only removing a set of density
$1/(2(\ell +m ))$
from
$A_1 \cup A_2$
. Finally, we claim there is no infinite set
$B\subset {\mathbb N}$
satisfying
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}\subset A'$
. Indeed, given such an infinite set B we can consider an infinite subset
$B' \subset B$
with all its elements equivalent modulo
$2(\ell +m )$
. That is, there exists
$j\in \{0,1,\dots ,2(\ell +m )-1\}$
so that
$b'\equiv j \pmod {2(\ell +m )}$
, for any
$b'\in B'$
. But then we have
$\{mb_1 + \ell b_2 : b_1,b_2 \in B'\ \text {and}\ b_1 \leq b_2\}\subset 2(\ell +m ){\mathbb N}+(\ell +m )j.$
Depending on the parity of j this either implies that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B'\ \text {and}\ b_1 \leq b_2\}\subset A_1$
or
$\{mb_1 + \ell b_2 : b_1,b_2 \in B'\ \text {and}\ b_1 \leq b_2\}\subset A_2$
, both of which are contradictions to the first part of the construction.
Remark 6.6. We stress that for both sets
$A,A'$
above we actually have that their natural densities are realised. This was to be expected because of Theorem 6.3. Indeed, we could not have, for example, a set
$A\subset {\mathbb N}$
with
$\underline {\mathop {}\!\mathrm {d}}(A)=1/2$
but
$\overline {\mathop {}\!\mathrm {d}}(A)>1/2$
(i.e., the natural density of A not realised) and also such that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}+t \not \subset A$
for any infinite set B and any integer
$t\in {\mathbb N}$
, because this would violate part
$(1)$
of Theorem 6.3.
7 Remarks and questions about further extensions
A significant part of this work was focused on extensions of Theorem 1.2 by relaxing the restrictions imposed on the sumsets involved. In short, we managed to provide complete characterisation for the existence of the patterns
$\{mb_1 + \ell b_2: b_1,b_2\in B\ \text {and}\ b_1\leq b_2 \}$
for infinite
$B\subset {\mathbb N}$
in shifts of a set
$A\subset {\mathbb N}$
, based on the values for the upper and lower asymptotic densities of A.
Another direction could be to consider patterns of the form
$\{mb_1 + \ell b_2: b_1,b_2\in B\ \text {and}\ b_1\neq b_2 \}$
. We recall Remark 1.3, according to which an assumption of positive upper density is not sufficient to find shifts of such infinite sumsets in a subset of the integers (unless, of course,
$\ell =m$
). A natural question, then, is if this problem has a ‘density solution’. We present two related constructions (which, we believe, can not be improved) and then state the question precisely.
Proposition 7.1. Let
$\ell ,m \in {\mathbb N}$
be distinct with
$\ell>m$
. There exist two sets
$A, A'\subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)=\ell /(\ell +m)$
and
$\overline {\mathop {}\!\mathrm {d}}(A')=1-m/(\ell +m)^2$
such that for any infinite set
$B\subset {\mathbb N}$
and any
$t\in {\mathbb N}$
we have
$\{mb_1 + \ell b_2: b_1,b_2\in B\ \text {and}\ b_1\neq b_2 \} \not \subset A-t$
and
$\{mb_1 + \ell b_2: b_1,b_2\in B\ \text {and}\ b_1\neq b_2 \} \not \subset A'$
.
Remark 7.2. It may be interesting to compare these bounds with the optimal bounds established for the sumsets
$\{mb_1 + \ell b_2 \colon b_1,b_2 \in B,\ \text {and}\ b_1\leq b_2\}$
in Theorems 1.7, 1.8 and Proposition 5.1. In particular, by assumption we have that
$k=m/\ell <1$
and then
$\ell /(\ell +m)=1/(k+1)$
, and this is greater than
$(k+1)/(k+2)$
, whenever
$k(k+1)<1$
. Also,
$1-m/(\ell +m)^2$
is greater than
$1-1/(\ell (k+1)(k+2))=1-1/((\ell +m)(k+2))$
, again, precisely when
$k(k+1) < 1$
.
The surprising fact that springs from this observation is the following; Say, without loss of generality, that
$\ell>m$
. Then, the largest bounds (we can find) for the value of upper density for a set that doesn’t contain sumsets of the form
$\{mb_1 + \ell b_2 \colon b_1,b_2 \in B,\ \text {and}\ b_1 \neq b_2\}$
are greater than the optimal bounds for a set that doesn’t contain sumsets
$\{mb_1 + \ell b_2 \colon b_1,b_2 \in B,\ \text {and}\ b_1 \leq b_2\}$
whenever
$\ell /m=1/k$
is greater than the Golden ratio! The relation between the bounds is reversed if
$\ell /m=1/k$
is less than the Golden ratio and the same comparisons hold for unshifted patterns.
We can also compare the bounds of Proposition 7.1 with the ones from the aforementioned results, but for the sumsets
$\{\ell b_1+mb_2 \colon b_1,b_2\in B\ \text {and}\ b_1\leq b_2\}$
. In this case, the comparison is not nearly as mystical, for the latter sumsets cannot be found in sets of upper density up to
$(k^{-1}+1)/(k^{-1}+2)$
and
$1-1/(m(k^{-1}+1)(k^{-1}+2))$
, for the cases of shift and no shift, respectively. But both of these are larger than the respective bounds from Proposition 7.1, that is,
$\ell /(\ell +m)$
and
$1-m/(\ell +m)^2$
.
Proof of Proposition 7.1.
The proof has similar features to the proofs of Propositions 5.1 and 6.5, so we try to ease exposition by avoiding repetitive arguments.
We consider the set
$A\subset {\mathbb N}$
defined by
$$ \begin{align*}A = {\mathbb N} \cap \bigcup_{n \in {\mathbb N}} [(\ell/m)^{2n}, (\ell/m-1/n) \cdot (\ell/m)^{2n})\end{align*} $$
Similarly to the proof of Proposition 5.1 we see that
$\overline {\mathop {}\!\mathrm {d}}(A)=\ell /(\ell +m)$
. We claim that there is no infinite set
$B\subset {\mathbb N}$
and integer
$t\in {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1,b_2\in B\ \text {and}\ b_1\neq b_2 \} \not \subset A-t$
.
Indeed, say
$B\subset {\mathbb N}$
is an infinite set and
$t\in {\mathbb N}$
an integer negating the claim. Then, for any
$b_1\in B$
we may choose
$b_2\in B$
arbitrarily large with respect to
$b_1$
and note that
$\alpha =mb_1+\ell b_2$
,
$\beta =mb_2 + \ell b_1 \in A-t$
. We observe that
$\alpha =(\ell /m)\beta - (\ell ^2/m-m)b_1$
and so we can choose
$b_2$
so large that
$c(b_1):=(\ell ^2/m-m)b_1$
is negligible (in a way to be made precise below) with respect to
$\alpha $
.
Let
$n\in {\mathbb N}$
be such that
$\alpha \in [(\ell /m)^{2n}, (\ell /m-1/n) \cdot (\ell /m)^{2n})-t$
. Then,
$$ \begin{align*}\beta = \frac{1}{(\ell/m)}\left(\alpha+c(b_1)\right) \in [(\ell/m)^{2n-1}, (\ell/m-1/n) \cdot (\ell/m)^{2n-1}) + \frac{(c(b_1)-t)}{(\ell/m)}\end{align*} $$
and we choose
$b_2$
large enough so that
$n\in {\mathbb N}$
is in turn large enough in order for the above to imply that
$\beta + t \in [(\ell /m)^{2n-1}, (\ell /m)^{2n}),$
hence
$\beta \notin A-t$
, a contradiction.
We finally consider the set
$A'=A \cup \left ( \bigcup _{j=1}^{\ell +m-1} (\ell +m){\mathbb N}+j \right )$
and arguing as in the proof of Proposition 5.1 we see that
$\overline {\mathop {}\!\mathrm {d}}(A)=1-m/(\ell +m)^2$
and that there is no infinite set
$B\subset {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1,b_2\in B\ \text {and}\ b_1\neq b_2 \} \subset A'.$
Remark. Observe that the set
$A\subset {\mathbb N}$
above is thick and as such
${\mathop {}\!\mathrm {d}}^{*}(A)=1$
.
Despite the urge to make a conjecture, due to limited dynamical as well as combinatorial evidence – apart from the very interesting Remark 7.2, which hints that the bounds of Proposition 7.1 may not be unrelated to the optimal bounds – we constrain ourselves to asking the following question.
Question 7.3. Let
$\ell ,m \in {\mathbb N}$
be distinct with
$\ell>m$
and let
$A\subset {\mathbb N}$
.
-
(i) If
$\overline {\mathop {}\!\mathrm {d}}(A)>\ell /(\ell +m)$
, does there exist an infinite set
$B\subset {\mathbb N}$
and some
$t\in {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1,b_2\in B\ \text {and}\ b_1\neq b_2 \}+t \subset A$
? -
(ii) If
$\overline {\mathop {}\!\mathrm {d}}(A)>1-m/(\ell +m)^2$
, does there exist an infinite set
$B\subset {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1, b_2\in B\ \text {and}\ b_1\neq b_2 \} \subset A$
?
With the sets constructed in Proposition 7.1 as a basis, we can mimic the argument from the proof of Proposition 6.5 and recover the following result.
Proposition 7.4. Let
$\ell ,m\in {\mathbb N}$
be distinct with
$\ell>m$
. There exist two sets
$A,A'\subset {\mathbb N}$
with
$\underline {\mathop {}\!\mathrm {d}}(A)=1/2$
and
$\underline {\mathop {}\!\mathrm {d}}(A')=1-1/(2(\ell +m))$
such that for any infinite set B and any integer
$t\in {\mathbb N}$
we have that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \neq b_2\}+t \not \subset A$
and
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \neq b_2\} \not \subset A'.$
Proof. Let
$A_1 , A_2 \subset {\mathbb N}$
be defined by
$$ \begin{align*}A_1 = {\mathbb N} \cap \bigcup_{n \in {\mathbb N}} [(\ell/m)^{2n}, (\ell/m-1/n) \cdot (\ell/m)^{2n})\end{align*} $$
and
$$ \begin{align*}A = {\mathbb N} \cap \bigcup_{n \in {\mathbb N}} [(\ell/m+1/n)\cdot (\ell/m)^{2n}, (\ell/m)^{2(n+1)}).\end{align*} $$
By the proof of Proposition 7.1 and a symmetrical argument for
$A_2$
, neither of the sets contains a sumset of the form
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \neq b_2\}+t$
, for any infinite
$B\subset {\mathbb N}$
and any
$t\in {\mathbb N}$
. Then, analogously to the proof of Proposition 6.5, we define
$A=(A_1\cap 2{\mathbb N}) \cup (A_2\cap (2{\mathbb N}+1))$
and
$A'=(A_1 \setminus 2(\ell +m){\mathbb N}) \cup (A_2 \setminus (2(\ell +m){\mathbb N}+(\ell +m)))$
and the claimed properties of
$A,A'$
follow similarly to the proof of Proposition 6.5.
Therefore, we also ask the following.
Question 7.5. Let
$\ell ,m \in {\mathbb N}$
be distinct and let
$A\subset {\mathbb N}$
.
-
(i) If
$\underline {\mathop {}\!\mathrm {d}}(A)>1/2$
, does there exist an infinite set
$B\subset {\mathbb N}$
and some
$t\in {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1, b_2\in B\ \text {and}\ b_1\neq b_2 \}+t \subset A$
? -
(ii) If
$\underline {\mathop {}\!\mathrm {d}}(A)>1-1/(2(\ell +m))$
, does there exist an infinite set
$B\subset {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1, b_2\in B\ \text {and}\ b_1\neq b_2 \} \subset A$
?
Provided Question 7.3 has a positive answer one should also inquire about the completely unrestricted problem, that is, the existence of infinite sumsets
$mB+\ell B=\{mb_1 + \ell b_2: b_1,b_2\in B\}$
. To this end, we ask two more questions after making an observation which follows from current results.
Proposition 7.6. Let
$\ell ,m\in {\mathbb N}$
be distinct with
$m>\ell $
and let
$k=m/\ell $
. Then, there exist sets
$A,A' \subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)=(k+1)/(k+2)$
and
$\overline {\mathop {}\!\mathrm {d}}(A')=1-1/\left (\ell (k+1)(k+2)\right )$
such that for any infinite set B and any integer
$t\in {\mathbb N}$
we have that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\}+t \not \subset A$
and
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\} \not \subset A'.$
Proof. All we need to observe is that both sumsets
$ \{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}$
and
$\{\ell b_1 + m b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}$
are contained in
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\} $
, for any
$B\subset {\mathbb N}$
, and so we can reduce to Proposition 5.1. Indeed, if a set fails to contain either of the former sumsets, then it will also fail to contain
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}$
. Now, as
$k>1$
, we have that
$$ \begin{align*}\max\{(k+1)/(k+2),(k^{-1}+1)/(k^{-1}+2)\} = (k+1)/(k+2),\end{align*} $$
and so it follows by Proposition 5.1 that there exists a set
$A\subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)=(k+1)/(k+2)$
and such that for any infinite
$B\subset {\mathbb N}$
and
$t\in {\mathbb N}$
we have that
$\{m b_1 + \ell b_2 : b_1,b_2 \in B\ \text {and}\ b_1 \leq b_2\}+t \not \subset A$
. In particular, it follows that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\} \not \subset A-t$
. The existence of
$A'$
is proved following the exact same argument and using the set
$A'$
provided by Proposition 5.1.
Repeating the same observation for values of lower density and Proposition 6.5 we have the following proposition.
Proposition 7.7. Let
$\ell ,m\in {\mathbb N}$
. There exist two sets
$A,A'\subset {\mathbb N}$
with
$\underline {\mathop {}\!\mathrm {d}}(A)=1/2$
and
$\underline {\mathop {}\!\mathrm {d}}(A')=1-1/(2(\ell +m))$
such that for any infinite set B and any integer
$t\in {\mathbb N}$
we have that
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\} \not \subset A-t$
and
$\{mb_1 + \ell b_2 : b_1,b_2 \in B\} \not \subset A'.$
It would be surprising if either of the next questions had a negative answer, but apart from our inability to improve on the previous constructions there is no evidence suggesting the opposite.
Question 7.8. Let
$\ell ,m \in {\mathbb N}$
be distinct with
$m>\ell $
and let
$k=m/\ell $
. Let also
$A\subset {\mathbb N}$
.
-
(i) If
$\overline {\mathop {}\!\mathrm {d}}(A)>(k+1)/(k+2)$
, does there exist an infinite set
$B\subset {\mathbb N}$
and some
$t\in {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1,b_2\in B\}+t \subset A$
? -
(ii) If
$\overline {\mathop {}\!\mathrm {d}}(A)>1-1/\left (\ell (k+1)(k+2)\right )$
, does there exist an infinite set
$B\subset {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1,b_2\in B\} \subset A$
?
Question 7.9. Let
$\ell ,m \in {\mathbb N}$
be distinct and
$A\subset {\mathbb N}$
.
-
(i) If
$\underline {\mathop {}\!\mathrm {d}}(A)>1/2$
does there exist an infinite set
$B\subset {\mathbb N}$
and some
$t\in {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1,b_2\in B \}+t \subset A$
? -
(ii) If
$\underline {\mathop {}\!\mathrm {d}}(A)>1-1/(2(\ell +m))$
does there exist an infinite set
$B\subset {\mathbb N}$
such that
$\{mb_1 + \ell b_2: b_1,b_2\in B\} \subset A$
?
As the above exposition on unrestricted sumsets
$mB+\ell B$
focused on the case of distinct
$\ell $
and m, we want to highlight that, since
$\{mb_1 + mb_2 \colon b_1,b_2 \in B\ \text {and}\ b_1\leq b_2 \}=mB+mB$
, the special unrestricted sumsets of the form
$mB+m B$
are already covered in Theorems 1.7, 1.8, Corollary 6.4 and Propositions 5.1, 6.5. In particular, for some
$A\subset {\mathbb N}$
and
$m\in {\mathbb N}$
we have the following implications, all of which are optimal.
-
(i) If
$\overline {\mathop {}\!\mathrm {d}}(A)>2/3$
, there exist some infinite set
$B\subset {\mathbb N}$
and some
$t\in \{0,1,\ldots ,2m-1\}$
such that
$mB+mB+t \subset A$
. -
(ii) If
$\overline {\mathop {}\!\mathrm {d}}(A)>1-1/(6m)$
, there exists some infinite set
$B\subset {\mathbb N}$
such that
$mB+mB \subset A$
. -
(iii) If
$\underline {\mathop {}\!\mathrm {d}}(A)>1/2$
, there exist some infinite set
$B\subset {\mathbb N}$
and some
$t\in \{0,1,\ldots ,2m-1\}$
such that
$mB+mB+t \subset A$
. -
(iv) If
$\underline {\mathop {}\!\mathrm {d}}(A)>1-1/(4m)$
, there exists some infinite set
$B\subset {\mathbb N}$
such that
$mB+mB \subset A$
.
We note that the bound in
$(i)$
does not depend on m, because the optimal bound established in Theorem 1.7 explicitly depends only on the ratio
$k=m/\ell $
, which in this case is always
$1$
. This suggests that perhaps
$(i)$
above already follows from Theorem 1.4, and this is indeed the case. The proof of this fact is nice and not very complicated, but serves no other purpose as to be included here. Similarly, using Theorem 1.4, one can prove that for any set
$A\subset {\mathbb N}$
with
$\overline {\mathop {}\!\mathrm {d}}(A)>5/6$
, there exists
$B\subset {\mathbb N}$
infinite and some
$t\in \{0,1,\ldots ,m-1\}$
such that
$mB+mB+t \subset A$
– note the difference for the range of the shift here – but of course, density larger than
$5/6$
is no longer sufficient for us to remove potential shifts, as the bounds in part
$(ii)$
above are optimal.
We finish with a proof of the last claim, showing that the range of shifts can be shortened. Observe that the set
$A\subset {\mathbb N}$
can be written as the disjoint union
$$ \begin{align*}A=m(A/m) \cup \left(m((A-1)/m)+1\right)\cup \dots \cup \left(m((A-(m-1))/m)+(m-1)\right),\end{align*} $$
where
$(A-i)/m=\{n\in {\mathbb N}: nm+i \in A\}$
and then
$m((A-i)/m)+i=A\cap (m{\mathbb N}+i)$
, for each
$i\in \{0,1,\ldots ,m-1\}$
. Moreover, it is easy to see that
$m \cdot \overline {\mathop {}\!\mathrm {d}}(m((A-i)/m))\leq \overline {\mathop {}\!\mathrm {d}}((A-i)/m)$
. Hence,
$$ \begin{align*}\overline{\mathop{}\!\mathrm{d}}(A) \leq \sum_{i=0}^{m-1} \overline{\mathop{}\!\mathrm{d}}(m((A-i)/m)) \leq \sum_{i=0}^{m-1} (\frac{1}{m}) \overline{\mathop{}\!\mathrm{d}}((A-i)/m).\end{align*} $$
As
$\overline {\mathop {}\!\mathrm {d}}(A)>5/6$
, the previous implies that
$\overline {\mathop {}\!\mathrm {d}}((A-i)/m)>5/6$
for some
$i\in \{0,1,\ldots ,m-1\}$
. Then, by Theorem 1.4, there exists an infinite set
$B\subset {\mathbb N}$
such that
$B+B\subset (A-i)/m$
, which means that
$m(B+B)+i \subset A$
, and
$i\in \{0,1,\ldots ,m-1\}$
.
Acknowledgements
The author is thankful to Joel Moreira, Nikos Frantzikinakis, Felipe Hernández, Tristán Radić, Vicente Saavedra-Araya and Andreas Mountakis for helpful comments on an earlier draft of this article and to the anonymous referees for their pertinent suggestions.
Competing interests
The author has no competing interests to declare.
Funding statement
The author was supported by the Warwick Mathematics Institute Centre for Doctoral Training.
Open access
