2.2 Simulation results under uniform inflow conditions

The inlet flow is maintained as $(U,0,0)$ , where $U=1.85~\text{m}~\text{s}^{-1}$ . The turbine is operated at the rotor frequency of 0.15–0.20 Hz, the corresponding $\unicode[STIX]{x1D6FA}=9.0$ to 12.0 expresses it in terms of revolutions per minute. The flow corresponding to $\unicode[STIX]{x1D6FA}=10.5~\text{r.p.m.}$ is treated as the representative case for which figure 1(a) shows the instantaneous axial velocity field in the $x{-}z$ plane passing through the turbine’s centre. It should be noted that owing to the uniform laminar inflow conditions, the wake flow evolution is slower here as compared to in cases of turbulent inflow conditions, such as in Churchfield et al. (Reference Churchfield, Li and Moriarty2013).

Figure 1. (a) The instantaneous axial velocity field in the $x{-}z$ plane passing through $y=0$ in $\unicode[STIX]{x1D6FA}=10.5$ case. The PSDs of $\tilde{w}$ -velocity fluctuations in the (b) near-wake region (the circles in panel a) show the tip and root vortices ( $\widetilde{f_{t}}=0.350~\text{Hz}$ ) and other near-wake vortices ( $\widetilde{f_{n}}\approx 0.219~\text{Hz}$ ), (c) far-wake region (the squares in panel a) show the far-wake oscillations have a broad peak at $\widetilde{f_{m}}\approx 0.048~\text{Hz}$ and (d) along the $x$ -direction (the crosses at $x/D=0.0$ , 2.5, 4.0, 6.0 and 9.0 in panel a) shows that the far-wake oscillations generate from amplification of the near-wake structures at 0.048 Hz ( $St\approx 0.52$ ).

In the near-wake region (up to $x/D\approx 4.5$ ), the velocity deficit is maximum in the core region ( $z/D\approx 0.325$ ) and is negligible in the area between the blade root and the nacelle. The tip and root vortices are present behind the blades in the immediate downstream region. Other vortices, called near-wake vortices here, also start to appear in the downstream region as indicated in the figure. The PSD in the near-wake region (panel b) shows peaks at $\widetilde{f_{t}}=0.350~\text{Hz}$ (root and tip vortices, $\widetilde{f_{t}}$ is twice the rotor frequency) and $\widetilde{f_{n}}\approx 0.219~\text{Hz}$ (near-wake vortices). Qualitatively, the near-wake region matches well with the LES results in Kumar & Mahesh (Reference Kumar and Mahesh2017) where a propeller’s geometry is fully resolved. We do not scrutinise the origin of near-wake structures here, which is a complex area of research as evident from the numerous studies (Widnall Reference Widnall1972; Okulov & Sørensen Reference Okulov and Sørensen2007; Felli, Camussi & Di Felice Reference Felli, Camussi and Di Felice2011; Hong et al. Reference Hong, Toloui, Chamorro, Guala, Howard, Riley, Tucker and Sotiropoulos2014). In this paper, we are concerned only with the effect of the obtained near-wake structures on the far-wake region.

The flow evolves and becomes turbulent in the far-wake region where a meandering pattern is observed (indicated in the figure). The PSDs in the far-wake region (panel c) show an increase in energy at all frequencies, which is due to the turbulence. More importantly, there is a peak at a low frequency ( $\widetilde{f_{m}}\approx 0.048~\text{Hz}$ ) that corresponds to the observed wake meandering. It should be noted that this peak is broad, i.e. it comprises a band of frequencies as also shown in panel (d) and figure 2, which hints that it is a result of convective instability (i.e. via the amplification of the upstream disturbances) (Huerre & Monkewitz Reference Huerre and Monkewitz1990). In order to trace the origin of the observed wake meandering, we plot $\unicode[STIX]{x1D719}_{w}$ at different streamwise locations in panel (d). In the later part of the near-wake region (at $x/D=2.5$ ), there are peaks at $\tilde{f}\approx 0.315~\text{Hz}$ , 0.219 Hz and their linear combinations. Successive $\unicode[STIX]{x1D719}_{w}$ at $x/D=4.0$ , 6.0 and 9.0 show the peak at 0.048 Hz gets amplified and this, we speculate, gives rise to the observed wake meandering in the far-wake region. When the frequency ( $\tilde{f}$ ) is non-dimensionalised as $St=\widetilde{f}D/U$ , $St_{m}\approx 0.52$ is found to be in the range observed in Mao & Sørensen (Reference Mao and Sørensen2018).

The origin of wake meandering via the amplification of near-wake structures is consistent with (i) the new mechanism discussed in § 1, (ii) convectively unstable nature of the flow shown in § 3 and (iii) the evolution of far-wake vortical structures in flows behind cylinders. Williamson & Prasad (Reference Williamson and Prasad1993) showed that in the far-wake region behind a cylinder (which is much further downstream than a turbine’s far-wake region), the flow amplifies a subharmonic component of the near-wake vortex shedding structure (particularly in the absence of other upstream perturbations) that gives rise to sustained vortical oscillations in the far-wake region. The results presented here show how near-wake structures can affect the far-wake region in flows behind turbines. This provides a plausible explanation for the hypotheses in Okulov & Sørensen (Reference Okulov and Sørensen2007), Iungo et al. (Reference Iungo, Viola, Camarri, Porté-Agel and Gallaire2013) and Viola et al. (Reference Viola, Iungo, Camarri, Porté-Agel and Gallaire2014), where they suggested that instabilities in the near-wake region can lead (or contribute) to meandering in the far-wake region.

Figure 2. (a,c,e,g) The instantaneous axial velocity fields in the $x{-}z$ plane at $y=0$ and corresponding (b,d,f,h) $\unicode[STIX]{x1D719}_{w}$ at $x/D=[2.5,4.0,6.0,9.0]$ and $z/D=0.325$ . Wake meandering is present in all the cases. Except for the $\unicode[STIX]{x1D6FA}=9.0~\text{r.p.m.}$ case, there is a peak in $\unicode[STIX]{x1D719}_{w}$ at $St\approx 0.5$ .

Figure 2(a,c,e,g) shows the non-dimensional instantaneous axial flow fields at increasing $\unicode[STIX]{x1D6FA}$ from the top to bottom. The flow fields show some level of meandering in all cases. It is relatively weak in the $\unicode[STIX]{x1D6FA}=9.0~\text{r.p.m.}$ case and gets stronger with increasing $\unicode[STIX]{x1D6FA}$ . This is consistent with the observations in Heisel et al. (Reference Heisel, Hong and Guala2018), where wake meandering is not observed for highly derated turbines, i.e. when the thrust coefficient becomes too small. The corresponding PSDs at $z/D=0.325$ at four streamwise locations $(x/D=\{2.5,4.0,6.0,9.0\})$ are presented in the adjacent plots (b,d,f,h). Except in the $\unicode[STIX]{x1D6FA}=9.0~\text{r.p.m.}$ case, there is a broad peak in $\unicode[STIX]{x1D719}_{w}$ at $St\approx 0.5$ . The fact that $St$ is nearly constant in all the cases suggests that the wake meandering frequency scales with the turbine diameter and the mean incoming velocity, as observed in Foti et al. (Reference Foti, Yang and Sotiropoulos2018b ) and others. The weak dependence of the peak frequency on $\unicode[STIX]{x1D6FA}$ shows the effect of the near-wake structures. This effect is expected to be small under turbulent inflow conditions.

2.3 Simulation results under sinusoidally varying inflow conditions

Turbines usually operate under turbulent inflow conditions where energetic structures from the boundary layer, upstream turbines, surface waves and other intermittent sources are present. Therefore, it is imperative to study the wake evolution under perturbed inflow conditions. In this paper, we limit ourselves to perturbations in the axial velocity that are spatially uniform and vary sinusoidally in time as $(U(1+A_{f}\sin (2\unicode[STIX]{x03C0}St_{f}(U/D)t)),0,0)$ , where $U$ is the same as before, $A_{f}$ and $St_{f}$ are the non-dimensional forcing amplitude and frequency, respectively. Although such a forcing is a poor approximation of turbulent inflow conditions for utility-scale turbines, many studies have shown harmonic response of a flow can provide valuable insights into instability generated flow structures. These include McKeon & Sharma (Reference McKeon and Sharma2010) for understanding the scaling of coherent structures in turbulent pipe flows and Garnaud et al. (Reference Garnaud, Lesshafft, Schmid and Huerre2013) for understanding the preferred mode selection in turbulent axisymmetric incompressible jets.

Figure 3. The instantaneous axial velocity fields under sinusoidally varying inflow conditions $St_{f}=$  (a–c) 0.11, (d–f) 0.43, (g–i) 0.76 and (j–l) 0.97. The forcing amplitudes (increasing from the bottom to top) are mentioned in the respective panels. The wake meandering pattern becomes regular (except for $St_{f}=0.11$ ) as $A_{f}$ increases.

We obtain the wake flow for the turbine operating at $\unicode[STIX]{x1D6FA}=10.5~\text{r.p.m.}$ under various $St_{f}$ and $A_{f}$ inflow conditions. Figure 3 presents the non-dimensional instantaneous axial velocity fields in the $x{-}z$ plane. The four columns correspond to four forcing frequencies, increasing from the left to right, while the forcing amplitudes (increasing from the bottom to top) are mentioned in the respective panels. In the absence of sinusoidal forcing, the far-wake oscillations result from the amplification of background noise (which includes the decomposing near-wake structures and the resulting turbulence). Consequently, the wake meandering pattern is irregular (figure 1 and the lowest row here) and its spectrum has a broad peak at $St_{m}$ (see figure 1 d). As $A_{f}$ is increased, the wake meandering pattern becomes regular (the top row except in the $St_{f}=0.11$ case) and the flow starts to exhibit periodic oscillations at $St_{f}$ (see figure 5). This phenomenon is similar to the lock-in observed in oscillators (Pikovsky, Rosenblum & Kurths Reference Pikovsky, Rosenblum and Kurths2001), where an oscillator starts to oscillate at the forcing frequency (provided the forcing amplitude is sufficiently high) in place of its natural frequency. We call it pseudo lock-in here because our flow is not an oscillator system, it is an amplifier of external disturbances. At pseudo lock-in, all other frequencies are suppressed (i.e. the given background noise is no longer amplified) and the wake flow starts to oscillate at the forcing frequency similar to a globally unstable flow.

Figure 4. The wake flow response to sinusoidal forcing in terms of $r_{f}=\unicode[STIX]{x1D719}_{w}(St_{f})/(\unicode[STIX]{x1D719}_{w}(St_{f})+\unicode[STIX]{x1D719}_{w}[St_{m}])$ , which is nearly zero when the effect of the background noise is dominant (i.e. $\unicode[STIX]{x1D719}_{w}[St_{m}]\gg \unicode[STIX]{x1D719}_{w}(St_{f})$ ) and approaches one as the effect of the sinusoidal forcing becomes dominant (i.e. $\unicode[STIX]{x1D719}_{w}(St_{f})\gg \unicode[STIX]{x1D719}_{w}[St_{m}]$ ). The black line represents the pseudo lock-in curve ( $r_{f}\approx 0.95$ ), above which the sinusoidal forcing has suppressed the effect of the background noise. Pseudo lock-in is achieved earlier (i.e. at lower $A_{f}$ ) when $St_{f}$ is closer to $St_{m}\;({\approx}0.52)$ .

We also see from figure 3 that the wake meandering pattern becomes regular at lower $A_{f}$ values when $St_{f}=0.43$ and 0.76 as compared to when $St_{f}=0.11$ and 0.97. Thus showing that pseudo lock-in is achieved earlier when $St_{f}$ is closer to $St_{m}$ . The variation in $A_{f}$ that is required to achieve pseudo lock-in with $St_{f}$ is shown in figure 4 for the $\unicode[STIX]{x1D6FA}=10.5~\text{r.p.m.}$ case. The colour map represents the ratio $r_{f}=\unicode[STIX]{x1D719}_{w}(St_{f})/(\unicode[STIX]{x1D719}_{w}(St_{f})+\unicode[STIX]{x1D719}_{w}[St_{m}])$ , where $\unicode[STIX]{x1D719}_{w}(St_{f})$ is the value of $\unicode[STIX]{x1D719}_{w}$ at $St_{f}$ (representing the wake flow response to the sinusoidal forcing) and $\unicode[STIX]{x1D719}_{w}[St_{m}]$ is the value of $\unicode[STIX]{x1D719}_{w}$ at the broadband peak near $St_{m}$ (representing the wake flow response to the background noise) calculated at $(x/D,z/D)=(9,0.325)$ . The black line represents the minimum $A_{f}$ required to achieve pseudo lock-in ( $r_{f}\approx 0.95$ ). The pseudo lock-in curve has a parabola-like shape with a minimum at $St_{f}\approx 0.54{-}0.65$ , which is close to $St_{m}\approx 0.52$ , and a little tilt towards $St_{f}>St_{m}$ . The hollow circles indicate the locations where the calculations are performed, $\unicode[STIX]{x1D719}_{w}$ at many points in figure 4 are calculated using only 400 s of data. The purpose here is to show the trend of pseudo lock-in, for which the accuracy of $\unicode[STIX]{x1D719}_{w}$ is not required.

Figure 5. The wake flow response to sinusoidal forcing at frequencies (a–c) 0.32, (d–f) 0.54 and (g–i) 0.76 and at varying $A_{f}$ (increasing from the bottom to top) in terms of the velocity fluctuations frequency spectra at $(x/D,z/D)=(9,0.325)$ . As $A_{f}$ increases, the maximum wake flow response shifts from at $St_{f}=0.76$ to at $St_{f}=0.32$ . Thus, showing a shift to lower frequencies with the increasing forcing amplitudes.

Quantitative response of the wake flow to sinusoidal forcing is calculated in terms of $E_{f}=(1/2U)\sqrt{|u|^{2}+|v|^{2}+|w|^{2}}$ , where ( $|u|,|v|,|w|$ ) are frequency spectra of the ( $\tilde{u} ,\tilde{v},\tilde{w}$ ) fluctuations, respectively. These calculations are performed using 1000 s of data sampled at 0.1 s. Figure 5 shows $E_{f}$ at $(x/D,z/D)=(9,0.325)$ for the $\unicode[STIX]{x1D6FA}=10.5~\text{r.p.m.}$ case, where the three columns correspond to three forcing frequencies (increasing from the left to right) and the three rows correspond to three forcing amplitudes (increasing from the bottom to top). A shift towards lower frequencies with increasing forcing amplitudes can be seen here. At the smallest forcing amplitude (bottom row), the maximum response is at the highest forcing frequency (i.e. $St_{f}=0.76$ ). At the medium and the largest forcing amplitudes, the maximum response shifts to $St_{f}=0.54$ and 0.32, respectively. This is in agreement with the findings of Mao & Sørensen (Reference Mao and Sørensen2018).

3.1 Local mean velocity profiles

We assume the mean flow to be axisymmetric around the $(y,z)=0$ axis and to be varying slowly in the $x$ -direction for the Wentzel–Kramers–Brillouin–Jeffrey (WKBJ) approximation to be valid. The mean axial ( $\overline{U}$ ) and azimuthal ( $\overline{W}$ ) velocities are then obtained by time averaging $\tilde{u} (x,0,z,t)$ and $\tilde{v}(x,0,z,t)$ , respectively, and are non-dimensionalised by the mean incoming velocity. Figure 6(a) presents $\overline{U}-1$ (blue lines) and $\overline{W}$ (red lines) at various streamwise locations for the $\unicode[STIX]{x1D6FA}=10.5~\text{r.p.m.}$ case. The velocity scales are shown at the top of the horizontal axis. The background colours here indicate the division between the near- and far-wake regions. In the near-wake region ( $x/D=0.0{-}4.5$ ), the mean axial velocity profiles show two regions of deficits similar to Foti et al. (Reference Foti, Yang, Campagnolo, Maniaci and Sotiropoulos2018a ) – the outer one due to the turbine blades and a smaller middle one due to the nacelle. Similarly, the azimuthal velocity has two regions as well – behind the blades it is in the opposite direction to the turbine rotation, while behind the nacelle it is smaller and in the same direction as the turbine rotation. The near-wake region is followed by the transition ( $x/D=4.5{-}5.5$ ), far-wake ( $x/D=5.5{-}9.5$ ) and buffer regions ( $x/D=9.5{-}10.0$ ). The mean velocity profiles in these regions do not have the middle wake and the shear layers are not as sharp as in the near-wake region.

Figure 6. Streamwise variation of the (a) local mean flow profile ( $\overline{U}-1$ : blue, $\overline{W}$ : red) and eigenfunction components (in the insets), (b) most amplified frequency, (c) spatial growth rate and (d) group velocity ( $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k|_{r}$ ) and diffusion term ( $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k^{2}|_{i}$ ) corresponding to $m=-1$ modes in the $\unicode[STIX]{x1D6FA}=10.5~\text{r.p.m.}$ case, unless explicitly mentioned.

3.3 Stability analysis results

We first heuristically define the concepts of convective and absolute instabilities and their relation to the global flow instability (for detailed reviews please see Huerre & Monkewitz (Reference Huerre and Monkewitz1990) and Chomaz (Reference Chomaz2005)). A parallel flow is linearly stable if $\unicode[STIX]{x1D714}_{i}<0$ for all values of $k$ , otherwise it is linearly unstable. In a linearly stable parallel flow, all external perturbations eventually die everywhere in the domain, whereas in a linearly unstable parallel flow, there are two possibilities. The first is the convective instability where perturbations of certain wavenumbers can grow but the growth rate is slower than the advection rate, i.e. perturbations get advected away from their origin. Mathematically, this happens when $\unicode[STIX]{x1D714}_{i}>0$ for some values of $k$ , but the modes with zero group velocity (i.e. $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k=0$ ) have $\unicode[STIX]{x1D714}_{i}<0$ . Such flows do not exhibit self-sustained oscillations but can greatly amplify external perturbations and are called amplifier flows. The second is the absolute instability where perturbations of certain wavenumbers can grow and the growth rate is faster than the advection rate (Tobias, Proctor & Knobloch Reference Tobias, Proctor and Knobloch1998) (i.e. at least one mode with $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k=0$ has $\unicode[STIX]{x1D714}_{i}>0$ ). Such flows exhibit self-sustained oscillations and are called oscillator flows.

These concepts of local stability analysis are applicable in weakly non-parallel flows where the basic flow varies on a longer length scale as compared to the instability wavelength (Monkewitz, Huerre & Chomaz Reference Monkewitz, Huerre and Chomaz1993; Chomaz Reference Chomaz2005). A weakly non-parallel flow is (i) stable – when it is locally linearly stable everywhere, (ii) an amplifier of external perturbations – when it is locally convectively unstable in some part of the domain, and (iii) an oscillator – when it is locally absolutely unstable in a sufficiently large region of the domain. A transition from stable to oscillator flow with increasing instability is shown in § 4.2.

Turbine wake flows are only locally convectively unstable (Iungo et al. Reference Iungo, Viola, Camarri, Porté-Agel and Gallaire2013; Mao & Sørensen Reference Mao and Sørensen2018) and thus belong to the second class (i.e. amplifier flow). In figure 6(b–d), therefore, we present the stability results corresponding to the locally most amplified modes (unless explicitly stated, the results are for $\unicode[STIX]{x1D6FA}=10.5~\text{r.p.m.}$ case and $m=-1$ mode). Panel (b) shows the variation of the most amplified frequency ( $\unicode[STIX]{x1D714}_{r}/2\unicode[STIX]{x03C0}$ ) with $x/D$ . The near-wake region of the flow amplifies higher frequencies (compared to the far-wake region) because the mean flow in this region has smaller-scale features (such as the middle wake) and sharper shear layers. The sudden changes in the frequency signify mode switchings (determined by the mean flow feature that is dominant locally). Again, we do not scrutinise the origin of different near-wake modes. In the transition region, there is a clear shift from the higher to lower frequencies. Finally, in the far-wake region, there is a slow but consistent decrease in the most amplified frequency. Panels (c) and (d) show the corresponding spatial growth rate ( $k_{i}$ ), the group velocity ( $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k|_{r}$ ), and the diffusion term ( $-10(\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k^{2})|_{i}$ ). The spatial growth rate has the same behaviour as $\unicode[STIX]{x1D714}_{sr}$ , it decreases slowly in the far-wake region as the flow evolves and the shear layers become less sharp. The group velocity signifies the advection rate of the perturbations and is roughly equal to 0.75 times the mean incoming velocity. The negative value of the diffusion term signifies that very high-frequency perturbations decay in the flow. The imaginary part of the group velocity ( $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k|_{i}$ ) at ( $\unicode[STIX]{x1D714}_{s},k_{s}$ ) is zero by definition, the linear dispersion term ( $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k^{2}|_{r}$ ) is negligibly small and the real wavenumber is given as $k_{sr}\approx \unicode[STIX]{x1D714}_{sr}(\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k)^{-1}$ (please see appendix A).

Additionally, in panel (a), we show the normalised eigenfunction components at locations $x/D=6$ , 7, 8 and 9 for the $m=0$ and $-1$ modes in terms of $\sqrt{u_{x}^{2}+u_{r}^{2}+u_{\unicode[STIX]{x1D703}}^{2}}$ from $r/D=0$ to 1.2. Both the modes initially show two peaks (at $r/D\approx 0.2$ and 0.5), but later at $x/D=9.0$ , only the outer peak at $r/D\approx 0.5$ survives. The eigenfunctions show the flow region in the radial direction where the wake meandering is influential (see (4.5)). In panel (b), we show the variation of the most amplified frequency in the $\unicode[STIX]{x1D6FA}=12.0~\text{r.p.m.}$ and 9.0 r.p.m. cases (only after their respective transition regions). The results for these flow cases are qualitatively similar, implications of this similarity are explored in § 5.1. In panel (c), we show the spatial growth rates for the $m=1$ , 0 and $-2$ modes, which indicate that the local stability results are very similar for all the azimuthal modes (see § 4.2).

4.1 Model deduction

Strictly, the CGL equation is limited to describing instability waves in flows that are (i) weakly nonlinear and (ii) weakly non-parallel (Aranson & Kramer Reference Aranson and Kramer2002; van Saarloos Reference van Saarloos2003). The first condition is satisfied when a flow is only marginally unstable (i.e. has just transited to the oscillator regime) and ensures the absence of the higher harmonics. The second condition ensures that instability waves satisfy the local dispersion relations as per the WKBJ approximation (Monkewitz et al. Reference Monkewitz, Huerre and Chomaz1993). Thus, it provides a way to obtain the linearised CGL coefficients from the local stability results (Le Dizès et al. Reference Le Dizès, Huerre, Chomaz and Monkewitz1996) as

(4.2) $$\begin{eqnarray}\displaystyle \dot{\tilde{A}} & = & \displaystyle -1\text{i}\left(\unicode[STIX]{x1D714}_{0}(X)+\frac{1}{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k^{2}}(\unicode[STIX]{x1D714}_{0},k_{0};X)k_{0}(X)^{2}\right)\tilde{A}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k^{2}}(\unicode[STIX]{x1D714}_{0},k_{0};X)k_{0}(X)\unicode[STIX]{x2202}_{x}\tilde{A}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1\text{i}}{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k^{2}}(\unicode[STIX]{x1D714}_{0},k_{0};X)\unicode[STIX]{x2202}_{x}^{2}\tilde{A},\end{eqnarray}$$

where $X\equiv \unicode[STIX]{x1D716}x$ ( $\unicode[STIX]{x1D716}\ll 1$ ) is the slow scale at which the basic flow varies, $\unicode[STIX]{x1D714}_{0}(X)$ and $k_{0}(X)$ are the complex frequency and wavenumber, respectively, at $X$ corresponding to the zero group velocity modes (i.e. $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k(\unicode[STIX]{x1D714}_{0},k_{0};X)=0$ ) and $\tilde{A}$ is the linear counterpart of $A$ . Following Crighton & Gaster (Reference Crighton and Gaster1976), Monkewitz et al. (Reference Monkewitz, Huerre and Chomaz1993) and Siconolfi et al. (Reference Siconolfi, Citro, Giannetti, Camarri and Luchini2017), linear self-sustained oscillations in a weakly non-parallel flow can be approximated as

(4.3) $$\begin{eqnarray}\tilde{A}(x,r,\unicode[STIX]{x1D703},t)=W_{g}(X)q_{g}(r,\unicode[STIX]{x1D703};X)\exp \left[\text{i}\unicode[STIX]{x1D716}^{-1}\int ^{X}k_{g}(X^{\prime })\,\text{d}X^{\prime }-\text{i}\unicode[STIX]{x1D714}_{g}t\right],\end{eqnarray}$$

where $W_{g}(X)$ is the slow amplitude variation, $q_{g}(r,\unicode[STIX]{x1D703};X)$ and $k_{g}(X)$ are the local eigenfunction and wavenumber, respectively, corresponding to the complex global mode frequency $\unicode[STIX]{x1D714}_{g}$ . In order to check the applicability of (4.2), we insert (4.3) in (4.2) and retain only the leading-order terms (at $O(\unicode[STIX]{x1D716}^{0})$ ). The resultant equation is the local linear dispersion relation at $X$ up to the second-order term as

(4.4) $$\begin{eqnarray}\unicode[STIX]{x1D714}_{g}-\unicode[STIX]{x1D714}_{0}(X)=\frac{1}{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k^{2}}(\unicode[STIX]{x1D714}_{0},k_{0};X)(k_{g}(X)-k_{0}(X))^{2}.\end{eqnarray}$$

Although, in general, flows have higher-order terms in their dispersion relations, they can be neglected because in a weakly non-parallel flow $\unicode[STIX]{x1D714}_{g}$ is close to $\unicode[STIX]{x1D714}_{0}(X)$ (Chomaz et al. Reference Chomaz, Huerre and Redekopp1991; Monkewitz et al. Reference Monkewitz, Huerre and Chomaz1993; Le Dizès et al. Reference Le Dizès, Huerre, Chomaz and Monkewitz1996; Pier & Huerre Reference Pier and Huerre2001; Pier Reference Pier2002).

In contrast to self-sustained oscillations modelled by (4.2), wake meandering arises from amplification of upstream disturbances (see §§ 1 and 2). We argue that (i) the CGL equation can still be used to model wake meandering and (ii) its coefficients can still be obtained from local stability results. In support of the first argument, Cossu & Chomaz (Reference Cossu and Chomaz1997), Tobias et al. (Reference Tobias, Proctor and Knobloch1998) and Bagheri et al. (Reference Bagheri, Henningson, Hœpffner and Schmid2009) showed that flow structures arising from the amplification of upstream perturbations can be qualitatively modelled using the CGL equation. In support of the second argument, Gaster (Reference Gaster1969) showed that spatially amplified modes can be modelled using a wave equation tuned by local mean flow parameters. More formally, Chomaz (Reference Chomaz2005) and Viola, Arratia & Gallaire (Reference Viola, Arratia and Gallaire2016) showed that similar to (4.3), the linear response to sinusoidal forcing (say at frequency $\unicode[STIX]{x1D714}_{f}$ ) in weakly non-parallel flows can be approximated as

(4.5) $$\begin{eqnarray}\tilde{A}(x,r,\unicode[STIX]{x1D703},t)=W_{f}(X)q_{f}(r,\unicode[STIX]{x1D703};X)\exp \left[\text{i}\unicode[STIX]{x1D716}^{-1}\int ^{X}k_{f}(X^{\prime })\,\text{d}X^{\prime }-\text{i}\unicode[STIX]{x1D714}_{f}t\right],\end{eqnarray}$$

where $W_{f}$ is the slow amplitude variation, $q_{f}(r,\unicode[STIX]{x1D703};X)$ and $k_{f}(X)$ are the local eigenfunction and wavenumber, respectively, corresponding to $\unicode[STIX]{x1D714}_{f}$ . The range of $\unicode[STIX]{x1D714}_{f}$ that is of interest is where the spatial amplification is maximum, which is at $\unicode[STIX]{x1D714}_{s}(X)$ (see § 3.3). The CGL equation to describe the spatially amplified waves, therefore, should be based on the dispersion relation around $(\unicode[STIX]{x1D714}_{s},k_{s})$ (see appendix A) and can be written as

(4.6) $$\begin{eqnarray}\displaystyle {\dot{A}} & = & \displaystyle -1\text{i}\left(\unicode[STIX]{x1D714}_{s}(X)-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k}(\unicode[STIX]{x1D714}_{s},k_{s};X)k_{s}(X)+\frac{1}{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k^{2}}(\unicode[STIX]{x1D714}_{s},k_{s};X)k_{s}(X)^{2}\right)A\nonumber\\ \displaystyle & & \displaystyle -\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k}(\unicode[STIX]{x1D714}_{s},k_{s};X)-\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k^{2}}(\unicode[STIX]{x1D714}_{s},k_{s};X)k_{s}(X)\right)\unicode[STIX]{x2202}_{x}A+\frac{1\text{i}}{2}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k^{2}}(x)\unicode[STIX]{x2202}_{x}^{2}A-C_{n}(X)|A|^{2}A.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

It should be noted here that we replaced $\tilde{A}$ by its nonlinear counterpart $A$ and also included the nonlinear term ( $C_{n}\equiv c_{nr}+\text{i}c_{ni}$ ). The conversion from the linear to nonlinear CGL equation in not trivial and is discussed in detail in § 5.2.

Equation (4.6) is solved in the range $X=0{-}12$ , where $X$ is equivalent to $x/D$ in the wake flow. At the inlet ( $X=0$ ), the boundary condition is set as time-dependent forcing, which can be an impulse, sinusoidal or white noise forcing or their combination. At the outlet ( $X=12$ ), following Heaton, Nichols & Schmid (Reference Heaton, Nichols and Schmid2009), the boundary condition is set as a convective outflow. We convert the partial differential equation to a set of ordinary differential equations by discretising the spatial coordinate using the fourth-order accurate central differencing scheme ( $\text{d}X=1/32$ ). We then use the implicit Crank–Nicolson scheme ( $\text{d}t=0.04$ ) for time marching and Picard’s method for iterating the nonlinear term.

4.2 Model coefficients

Figure 7. The coefficients are determined using least-square polynomial curve fits (red lines) to the local stability results at $m=-1$ (black lines) in the region $X=4.5{-}10.0$ .

Figure 7 shows the model coefficients ( $\unicode[STIX]{x1D714}_{sr}/2\unicode[STIX]{x03C0}$ , $k_{si}$ , $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k(\unicode[STIX]{x1D714}_{s},k_{s})|_{r}$ and $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k^{2}$ $(\unicode[STIX]{x1D714}_{s},k_{s})|_{i}$ ), which are determined directly by least-square polynomial curve fitting of the local stability results at $m=-1$ in the region $X=4.5{-}10.0$ (presented in figure 6). In the near-wake region ( $X<4.5$ ), the coefficients are extrapolated (as shown in the figure) such that the model response and turbine wake flow results roughly match in the region $X=2.0{-}3.0$ (see § 5.1). In principle, the model coefficients should be fixed separately for different azimuthal modes and thus different CGL equations should be used for the forced response based on the azimuthal wavenumber of the inflow disturbances. However, the stability results are very similar at all $m$ (as shown in figure 6 c). We, therefore, assume that a single CGL equation should be able to qualitatively model the evolution of all $m$ modes.

Figure 8. The linear impulse response of the system (a) decays monotonically (stable regime), (b) shows transient growth (amplifier regime – present case), (c) exhibits nearly self-sustained oscillations (marginally close to the oscillator regime) and (d) exhibits exponentially growing oscillations (oscillator regime). The lines correspond to the response amplitude at $X=\{1,2,3,\ldots ,10\}$ (the arrows indicate increasing $X$ ).

Figure 8 shows the linear impulse response of the model (panel b) as well as for its variants (panels a, cand d). An impulse of magnitude 1 is applied at $X=0$ at time $t=0$ , and the response amplitudes at $X=\{1,2,3,\ldots ,10\}$ with time are plotted. Panels (a–d) show transition from (a) the stable regime to (b) the amplifier regime to (c) being marginally close to the oscillator regime and finally to (d) the oscillator regime as the flow instability increases. In the stable regime in (a), a disturbance dies down monotonically. In the amplifier regime in (b), a disturbance shows a transient growth via a convective-type non-normality (Cossu & Chomaz Reference Cossu and Chomaz1997) before eventually decaying. The flow is still in the amplifier regime but is marginally close to the oscillator regime in (c). The transient growth in this case is much higher and the decay rate is much slower as compared to those in (b). Thus, even small external noise can sustain oscillations in such a flow (Huerre & Monkewitz Reference Huerre and Monkewitz1990; Babcock, Ahlers & Cannell Reference Babcock, Ahlers and Cannell1991). In the oscillator regime in (d), a disturbance grows exponentially until the nonlinearities saturate the oscillations to a finite amplitude. This figure confirms that, like the wake flow, the model (i) is in the amplifier regime and (ii) can spatially amplify the incoming disturbances.

The nonlinear saturation term ( $c_{nr}$ ) represents the reduction in amplification of disturbances with their amplitude. It is observed in § 2.3, that this reduction is higher at the higher forcing frequencies ( $St_{f}$ ). Thus, $c_{nr}$ should be proportional to a positive exponent of $St_{f}$ . Among the exponents tried (0.5, 1.0, 1.5 and 2.0), 1.5 gives the best results. Thus leading to $c_{nr}=4(2\unicode[STIX]{x03C0}St_{f})^{1.5}$ , where the pre-multiplication factor controls the level of the saturation. The nonlinear dispersion term ( $c_{ni}$ ) represents the change in the wavenumber with the forcing amplitude and, similar to the linear dispersion term, is set as zero. When a number of frequencies are present in the boundary forcing, the nonlinear saturation term is set as $c_{nr}(X)=4(2\unicode[STIX]{x03C0}(\unicode[STIX]{x1D6F4}_{j}A_{fj}St_{fj}G_{Lj}(X)/\unicode[STIX]{x1D6F4}_{j}A_{fj}G_{Lj}(X)))^{1.5}$ , where $A_{fj}$ and $G_{Lj}(X)$ are the forcing amplitude and the linear gain corresponding to the forcing frequency $St_{fj}$ (linear gains at some frequencies are shown in appendix B). The implications of the nonlinear coefficient and alternative ways for its mathematically rigorous calculation are discussed in § 5.2.

4.3 Model behaviour

Figure 9. The model response to white Gaussian noise forcing ( $A_{w}=0.0004$ ) in terms of the PSDs ( $\unicode[STIX]{x1D719}_{A}$ ) at $X=\{1,2,3,\ldots ,10\}$ . The oscillations evolve towards lower frequencies with increasing $X$ (indicated by the arrow) and finally have a broad peak at $St\approx 0.5$ .

Turbines operate under conditions comprising of small-scale turbulence as well as coherent structures arising from a number of sources. Therefore, we study the model behaviour when inflow conditions (at $X=0$ ) are set as combinations of white Gaussian noise (representing small-scale turbulence) and sinusoidal forcing (representing coherent structures). Although simplistic, such input–output analyses are shown to be useful in understanding the origin of complex structures arising in turbulent flows (see § 2.3).

Figure 9 shows the model response to white Gaussian noise forcing (of normalised amplitude $A_{w}=0.0004$ ) in terms of the PSDs at $X=\{1,2,3,\ldots ,10\}$ . The PSDs evolve towards lower frequencies and have a broad peak at $St\approx 0.5$ in the downstream region, which matches well with the wake flow PSDs shown in figure 1(d). The peak is broader here because the background noise is white, unlike in turbine far wake where it consists of the near-wake structures. In addition to the white noise, which is present in all the subsequent simulations, we add an upstream sinusoidal forcing term (of normalised amplitude $A_{f}$ and frequency $St_{f}$ ) at $X=0$ . Figure 10 shows the model responses to forcing at varying $St_{f}$ and $A_{f}$ in terms of $r_{fm}=\unicode[STIX]{x1D719}_{A}(St_{f})/\unicode[STIX]{x1D719}_{A}(St_{f})+\unicode[STIX]{x1D719}_{A}(St_{max})$ , where $\unicode[STIX]{x1D719}_{A}(St_{f})$ and $\unicode[STIX]{x1D719}_{A}(St_{max})$ are the PSD values (at $X=9$ ) at the forcing frequency ( $St_{f}$ ) and at the frequency ( $St_{max}$ ) where the response is maximum but $St_{max}\neq St_{f}$ . The ratio $r_{fm}$ is nearly zero when the background noise is dominant and approaches one as the sinusoidal forcing suppresses the effect of the background noise. The black line shows the pseudo lock-in curve ( $r_{fm}\approx 0.95$ ), i.e. the minimum $A_{f}$ at a given $St_{f}$ where the effect of the background noise is suppressed. Similar to that for the wake flow in figure 4, pseudo lock-in is achieved at lower $A_{f}$ when $St_{f}\approx 0.54{-}0.65$ , which is close to $St_{m}\approx 0.52$ , and the pseudo lock-in curve is parabola like in shape with a tilt towards $St_{f}>St_{m}$ .

Figure 10. The model response to sinusoidal forcing in terms of $r_{fm}$ , which is nearly zero when the background noise is dominant and approaches one as the sinusoidal forcing becomes dominant. The black line represents the pseudo lock-in curve ( $r_{fm}\approx 0.95$ ), above which the sinusoidal forcing has suppressed the effect of the background noise. Pseudo lock-in is achieved at lower $A_{f}$ when $St_{f}$ is close to $St_{m}\;({\approx}0.52)$ .

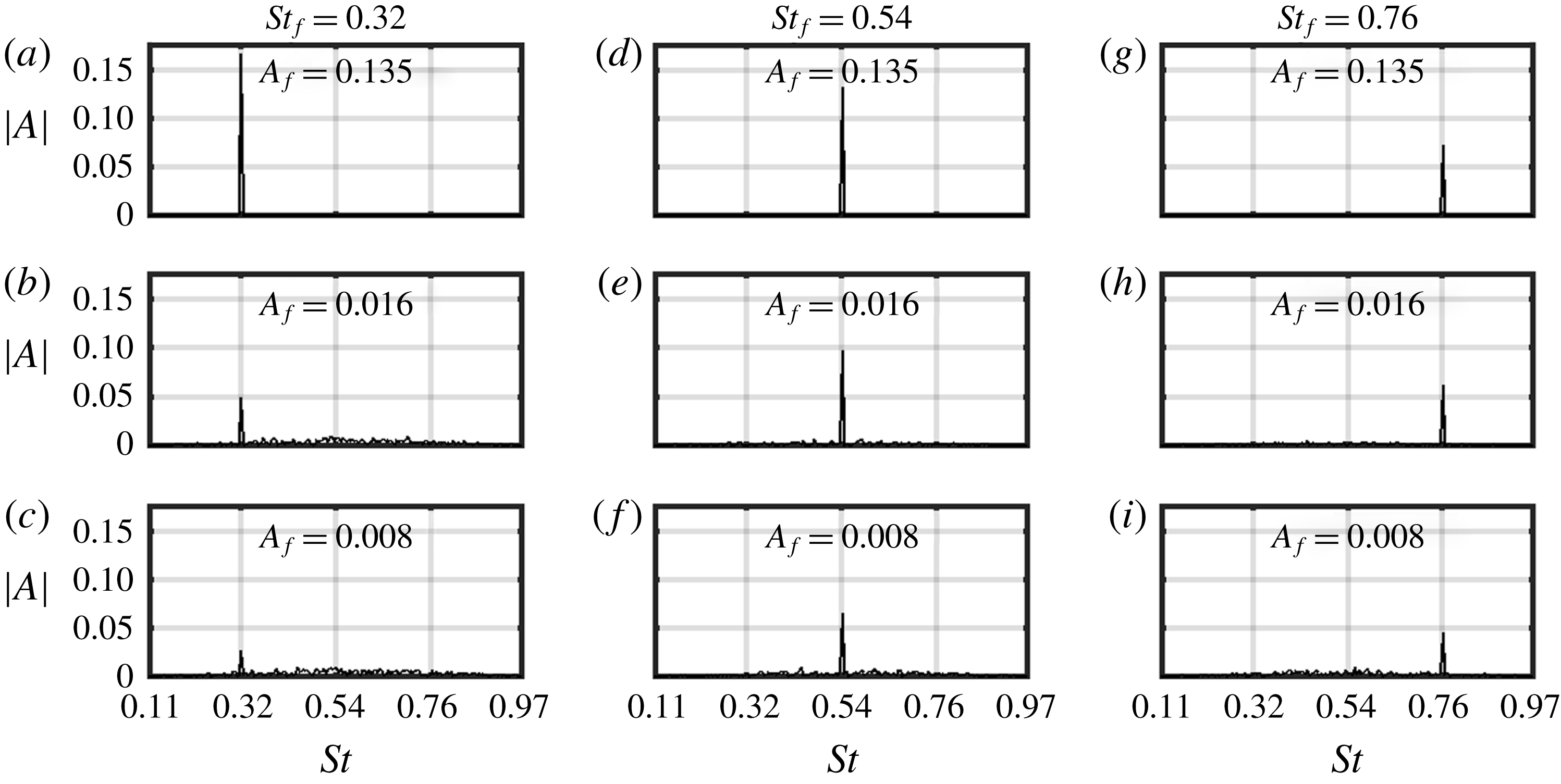
Figure 11. The model response to forcing at frequencies (a–c) 0.32, (d–f) 0.54 and (g–i) 0.76 and at varying $A_{f}$ (increasing from bottom to top) in terms of the spectra at $X=9$ . As $A_{f}$ increases, the maximum model response shifts from $St_{f}=0.54$ to $St_{f}=0.32$ . Thus showing a shift to lower frequencies with increasing forcing amplitude.

Figure 11 presents the model responses (in terms of the frequency spectrum at $X=9$ ) to sinusoidal forcing at varying $St_{f}$ (increasing from the left to right) and $A_{f}$ (increasing from the bottom to top). The maximum response shifts from $St_{f}=0.54$ to 0.32 as the forcing amplitude increases. This shows a shift towards lower frequencies with increasing $A_{f}$ , as also seen for the wake flow in figure 5 and Mao & Sørensen (Reference Mao and Sørensen2018).

5.1 Achievements of the low-order model

The match between figures 10 and 11 with figures 4 and 5, respectively, shows how well the CGL equation models the convectively amplified flow structures that give rise to wake meandering. Thus, justifying the use of the CGL equation (4.6) for modelling wake meandering. Here, we present a more detailed comparison between the model and the wake flow results. It should be noted that we only qualitatively model the wake from $x/D=4.5$ to 9.5. The quantitative match between the two arises because the model is designed to roughly match the wake flow in the region $x/D=2.0$ to 3.0. The model output $|A|$ is equivalent to the wake flow response amplitude calculated as the summation of $E_{f}$ at $St_{f}$ and its harmonics (see figure 5) and then averaged over $z/D=0.0{-}0.5$ .

5.1.1 Variations in the wake meandering features with the forcing parameters

Figure 12. Comparison of the wake flow and the model responses to forcing at frequencies (a,b) 0.32, (c,d) 0.54 and (e,f) 0.76 and at two forcing amplitudes. The wake meandering frequency shifts to lower values with increasing (i) $x/D$ and (ii) $A_{f}$ .

Figure 12 shows the variations of the wake flow and the model response amplitudes with the streamwise distance from the turbine. The results are presented for three forcing frequencies (increasing from left to right) and two forcing amplitudes (a,c,e– $A_{f}=0.016$ , b,d,f– $A_{f}=0.135$ ). There are two main points to note from this figure. The first is the change in the dominant frequency with the downstream distance. The top row shows that the response at $St_{f}=0.32$ increases in the streamwise direction up to $x/D\approx 10$ , while the responses at $St_{f}=0.54$ and $St_{f}=0.76$ initially increase up to $x/D\approx 9$ and $x/D\approx 7$ , respectively, and then decrease. Consequently, up to $x/D\approx 6$ , the wake flow response at $St_{f}=0.76$ is dominant while after that the response at $St_{f}=0.54$ is dominant. The bottom row shows qualitatively similar behaviour, where the wake flow response at $St_{f}=0.54$ is dominant initially (up to $x/D\approx 5$ ) while the response at $St_{f}=0.32$ is dominant later. This shows that as the wake evolves in the downstream direction, the frequency content shifts toward the lower values as also observed in Foti et al. (Reference Foti, Yang and Sotiropoulos2018b ). The physical origin of such behaviour is the mean flow evolution, which spreads in the radial direction with the downstream distance. Thus, the frequency of the locally most unstable mode decreases with $x/D$ (as shown in figure 6 b). Because the model coefficients are directly based on the local stability results, the model, apart from minor quantitative differences, mimics this wake flow behaviour correctly.

The second point to note is the change in the dominant frequency with the forcing amplitude. The figure shows that the wake flow responses at all three $St_{f}$ increase from the top to the bottom row as $A_{f}$ increases. This increment in the response is maximum at $St_{f}=0.32$ and is minimum at $St_{f}=0.76$ . Consequently, in the top row, the model response is maximum at $St_{f}=0.76$ (for $x/D<6$ ) and at $St_{f}=0.54$ (for $x/D>6$ ). While, in the bottom row, the model response is maximum at $St_{f}=0.54$ (for $x/D<5$ ) and at $St_{f}=0.32$ (for $x/D>5$ ). This shows that as the disturbance amplitude increases, the wake flow response shifts towards lower frequencies as also observed in Mao & Sørensen (Reference Mao and Sørensen2018). Again the model captures this behaviour correctly, thus, justifying our choice of the nonlinear coefficient (see § 4.2). The figure also shows that at the higher $A_{f}$ (bottom row), the wake flow response fluctuates around its curve fit. These fluctuations are because of the presence of the higher harmonics and their interaction with the fundamental mode. The higher harmonic was also observed in figure 5(a), but is not present in the CGL equation based model results (such as in figure 11 a). This is discussed in appendix B.

5.1.2 Variations in the wake meandering features with the turbine operating conditions

Figure 13. Same results as in figure 12 but for the $\unicode[STIX]{x1D6FA}=12.0~\text{r.p.m.}$ and 9.0 r.p.m. cases. A comparison between different $\unicode[STIX]{x1D6FA}$ cases shows that wake meandering (i) occurs earlier in the streamwise direction and (ii) has higher amplitude as $\unicode[STIX]{x1D6FA}$ increases (because the thrust coefficient increases with $\unicode[STIX]{x1D6FA}$ ). (iii) The Strouhal number range, however, remains nearly unaffected by changing $\unicode[STIX]{x1D6FA}$ . All these features are well captured by the low-order model.

Figure 13 presents the same results as in figure 12 but for the wake flows corresponding to $\unicode[STIX]{x1D6FA}=12.0~\text{r.p.m.}$ and 9.0 r.p.m. cases. A comparison of the wake flow behaviour for different $\unicode[STIX]{x1D6FA}$ cases reveal three important features. The wake meandering (i) occurs earlier in the streamwise direction, (ii) has higher amplitude and (iii) has nearly constant peak Strouhal number range as $\unicode[STIX]{x1D6FA}$ increases. The first two features are due to the fact that thrust coefficient ( $C_{t}$ ) increases with $\unicode[STIX]{x1D6FA}$ ( $C_{t}=\{0.59,0.74,0.86\}$ for $\unicode[STIX]{x1D6FA}=\{9.0~\text{r.p.m.},10.5~\text{r.p.m.},12.0~\text{r.p.m.}\}$ , respectively). While the third feature is because wake meandering frequency scales with the incoming velocity and turbine diameter, the operating conditions play only a marginal role.

Foti et al. (Reference Foti, Yang, Campagnolo, Maniaci and Sotiropoulos2018a ) performed LES on a turbine operating at optimal and suboptimal (lower thrust) conditions and simulated them with and without a nacelle. They observed that wake meandering is delayed when turbine is operating at suboptimal condition as well as when simulated without a nacelle (similar observations are also reported in Kang, Yang & Sotiropoulos (Reference Kang, Yang and Sotiropoulos2014)). They attributed this observation to the turbine drag force that determines the wake deficit and affects the mean velocity evolution. The local stability results in figure 6(b) also support this reasoning, where transition to the far-wake region occurs earliest in the $\unicode[STIX]{x1D6FA}=12.0~\text{r.p.m.}$ case and latest in the $\unicode[STIX]{x1D6FA}=9.0~\text{r.p.m.}$ case. Consequently, this observation is also reflected in the model, where (like the wake flow) the peak amplitude in each $A_{f}$ and $St_{f}$ case is achieved earliest in the $\unicode[STIX]{x1D6FA}=12.0~\text{r.p.m.}$ case and latest in the $\unicode[STIX]{x1D6FA}=9.0~\text{r.p.m.}$ case.

Higher drag force (or wake deficit) is also responsible for higher wake meandering amplitude. This is first shown in Yang et al. (Reference Yang, Howard, Guala and Sotiropoulos2015), where the added turbulent kinetic energy in the far-wake region is shown to increase with the thrust coefficient, and is later also confirmed in Heisel et al. (Reference Heisel, Hong and Guala2018) and Foti et al. (Reference Foti, Yang, Campagnolo, Maniaci and Sotiropoulos2018a ,Reference Foti, Yang and Sotiropoulos b ). Not shown in local stability results here, the spatial growth rate ( $-k_{si}$ ) also increases with $\unicode[STIX]{x1D6FA}$ , particularly in the region up to $x/D=6$ , and hence is also observed in the model results.

The results in figures 2, 12 and 13 show that the peak frequency does not vary much with the turbine’s operating conditions. The small increase in the peak frequency with increasing $\unicode[STIX]{x1D6FA}$ in figure 2 was attributed to the effect of the near-wake structures. In figures 12 and 13, there is a small reduction in the peak frequency with increasing $\unicode[STIX]{x1D6FA}$ . This reduction is attributed to the earlier onset of wake meandering in higher $\unicode[STIX]{x1D6FA}$ cases as is also reflected in the stability results in figure 6(b). These results thus corroborate that wake meandering frequency scales with the turbine diameter and the mean velocity.

5.2 System nonlinearity and transfer of energy from low to high frequencies

As mentioned at the end of § 4.1, the conversion from the linear to nonlinear CGL equation is not trivial. There are various options that exist in the literature. These include using (i) the nonlinear dispersion relations to obtain the CGL coefficients (Pier et al. Reference Pier, Huerre, Chomaz and Couairon1998), (ii) a weakly nonlinear analysis to obtain the nonlinear term from the Navier–Stokes equations (Sipp & Lebedev Reference Sipp and Lebedev2007), (iii) an input–output analysis to find the nonlinear terms as well as their order (Lee et al. Reference Lee, Zhu, Li and Gupta2019) and (iv) a self-consistent framework to obtain the variation in the nonlinear gain with the forcing amplitude (Mantič-Lugo & Gallaire Reference Mantič-Lugo and Gallaire2016). The first two methods are limited to self-sustained oscillations, while the latter two methods are computationally intensive as well as mathematically involved and hence are out of the scope of the present study. Here, we determine the nonlinear term to be proportional to $\unicode[STIX]{x1D714}_{f}^{1.5}$ based on the wake flow observations (see § 4.2). The results in figures 12 and 13 justify our choice of the nonlinear coefficient, as it correctly captures the change in wake meandering behaviour with the forcing amplitude. To further justify our choice of the nonlinear coefficient, we refer to the results in Keppens et al. (Reference Keppens, Tóth, Westermann and Goedbloed1999) where they showed the saturation amplitude to be higher at the lower wavenumbers (than the linearly most unstable wavenumber) in Kelvin–Helmholtz-type instabilities.

Physically, the origin of nonlinear saturation is the distortion of the base flow, which results in a mean flow profile that, via Reynolds stress, saturates the instability modes at finite amplitudes. This is first formulated by Stuart (Reference Stuart1960) and calculated recently by Mantič-Lugo, Arratia & Gallaire (Reference Mantič-Lugo, Arratia and Gallaire2014) and Meliga (Reference Meliga2017) for oscillator flows and, more relevant to the present case, by Mantič-Lugo & Gallaire (Reference Mantič-Lugo and Gallaire2016) for the response to harmonic forcing in an amplifier flow. Although, we do not obtain the nonlinear term from rigorous calculations. Nevertheless, based on the present results, we speculate that in the far-wake region higher-frequency flow structures distort the wake flow faster and create more Reynolds stress as compared to lower-frequency flow structures.

Another role of nonlinearity is to transfer energy between the different frequencies that are otherwise linearly decoupled. Heisel et al. (Reference Heisel, Hong and Guala2018) observed that very low-frequency disturbances transfer energy to relatively higher frequencies. We perturb the wake flow and the model by low-frequency disturbances (at $St_{f}=0.11$ ), and the spectra of their responses are shown in figure 14. Panel (a) shows that in the wake flow, energy is transferred to the higher frequencies and several peaks at the higher harmonics appear in the far-wake region. Panel (b) shows that in the model, energy from $St_{f}=0.11$ is also transferred to higher frequencies but there are no higher harmonic peaks in the far-wake region. This is because the CGL equation is inherently unable to capture the higher harmonics. An alternative to the CGL equation, in the form of a wave equation, that can capture the higher harmonics is formulated and discussed in appendix B.

Figure 14. The (a) wake flow and (b) model response to forcing at a low frequency ( $St_{f}=0.11$ ). They both show a transfer of energy from the low frequency (at $x/D=4$ ) to relatively higher frequencies at $St=0.2{-}0.8$ (at $x/D=9$ ). The model, however, is unable to account for the transfer of energy to the higher harmonics.

5.3 Limitations of the low-order model

The main limitation of the present model that hinders quantitatively accurate predictions arises from the limitations in our understanding of the near-wake region. In contrast to the far-wake region, the flow instabilities and their interactions in the near-wake region are very sensitive to the turbine design and support structures (Kumar & Mahesh Reference Kumar and Mahesh2017). Reliable modelling and understanding the origin of flow instabilities in this region, therefore, may require turbine-geometry resolved high-fidelity simulations. This is beyond the scope of this study and is the reason that we avoided speculation on the origin of the near-wake structures and mode switchings observed in §§ 2 and 3, respectively. The model coefficients in the near-wake region, therefore, are based only on extrapolation of the far-wake region (see § 4.2) and a rough match with the near-wake region (see § 5.1). Other limitations in the model arise from the strong nonlinearity (as discussed in § 5.2 and appendix B) and from lack of coupling of different azimuthal wavenumber modes.

Apart from that, there are limitations that arise from the simplifications in the simulations as compared to realistic conditions in utility-scale turbines. These include spatially uniform inflow conditions in place of a turbulent boundary layer mean flow profile or mean incoming flow at a yaw angle, which disrupt the axisymmetric nature of the flow. Other complexities, such as the spatial shape of turbulent structures, presence of support structures and further variations in the operating conditions increase the number of parameters to be considered in the model. To account for them, the present model may need data from input–output models developed in the literature (Hamilton et al. Reference Hamilton, Viggiano, Calaf, Tutkun and Cal2018).