We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .
To save content items to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
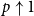 $p\uparrow 1$ limit
$p\uparrow 1$ limit
Let 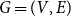 $G=(V,E)$ be a countable graph. The Bunkbed graph of
$G=(V,E)$ be a countable graph. The Bunkbed graph of 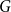 $G$ is the product graph
$G$ is the product graph 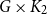 $G \times K_2$, which has vertex set
$G \times K_2$, which has vertex set 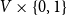 $V\times \{0,1\}$ with “horizontal” edges inherited from
$V\times \{0,1\}$ with “horizontal” edges inherited from 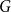 $G$ and additional “vertical” edges connecting
$G$ and additional “vertical” edges connecting 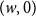 $(w,0)$ and
$(w,0)$ and 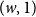 $(w,1)$ for each
$(w,1)$ for each 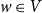 $w \in V$. Kasteleyn’s Bunkbed conjecture states that for each
$w \in V$. Kasteleyn’s Bunkbed conjecture states that for each 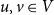 $u,v \in V$ and
$u,v \in V$ and 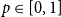 $p\in [0,1]$, the vertex
$p\in [0,1]$, the vertex 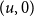 $(u,0)$ is at least as likely to be connected to
$(u,0)$ is at least as likely to be connected to 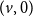 $(v,0)$ as to
$(v,0)$ as to 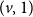 $(v,1)$ under Bernoulli-
$(v,1)$ under Bernoulli-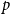 $p$ bond percolation on the bunkbed graph. We prove that the conjecture holds in the
$p$ bond percolation on the bunkbed graph. We prove that the conjecture holds in the 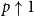 $p \uparrow 1$ limit in the sense that for each finite graph
$p \uparrow 1$ limit in the sense that for each finite graph 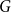 $G$ there exists
$G$ there exists 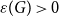 $\varepsilon (G)\gt 0$ such that the bunkbed conjecture holds for
$\varepsilon (G)\gt 0$ such that the bunkbed conjecture holds for 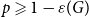 $p \geqslant 1-\varepsilon (G)$.
$p \geqslant 1-\varepsilon (G)$.
The origin of ionic conductivity in bulk lithium lanthanum titanate, a promising solid electrolyte for Li-ion batteries, has long been under debate, with experiments showing lower conductivity than predictions. Using first-principles-based calculations, we find that experimentally observed type I boundaries are more stable compared with the type II grain boundaries, consistent with their observed relative abundance. Grain boundary stability appears to strongly anti-correlate with the field strength as well as the spatial extent of the space charge region. Ion migration is faster along type II grain boundaries than across, consistent with recent experiments of increased conductivity when type II densities were increased.

Email your librarian or administrator to recommend adding this to your organisation's collection.