Branching process approximation to the initial stages of an epidemicprocess has been used since the 1950's as a technique for providing stochastic counterparts to deterministic epidemic threshold theorems.One way of describing the approximation is to construct both branching and epidemic processes on the same probability space, insuch a way that their paths coincide for as long as possible. Inthis paper, it is shown, in the context of a Markovian model of parasiticinfection, that coincidence can be achieved with asymptotically high probability until MN infections have occurred, as long asMN = o(N 2/3), where N denotes the total number of hosts.

We study the variance-to-mean ratio of the distributions of parasites among hosts for some models of parasite infection, using the cohort approach. We consider a model with density dependence in parasite mortality, and two different formulations of disease induced host mortality. We show that the distributions of parasites, conditional on host survival, converge to quasi-stationary distributions as host age increases. When there is density dependence in parasite mortality, the limiting variance-to-mean ratio is less than 1 (an ‘under-dispersed’ distribution). In contrast, the two modes of disease induced host mortality show that either over- or underdispersed distributions may result.

Stein's method is used to prove approximations in total variation to thedistributions of integer valued random variables by (possibly signed)compound Poisson measures. For sums of independent random variables,the results obtained are very explicit, and improve upon earlierwork of Kruopis (1983) and Čekanavičius (1997);coupling methods are used to derive concrete expressions for the errorbounds. An example is given to illustrate the potential for applicationto sums of dependent random variables.

It is well known that, in a Bienaymé-Galton–Watson process (Zn) with 1 < m = EZ1 < ∞ and EZ1 log Z1 <∞, the sequence of random variables Znm –n converges a.s. to a non–degenerate limit. When m =∞, an analogous result holds: for any 0< α < 1, it is possible to find functions U such that α n U (Zn) converges a.s. to a non-degenerate limit. In this paper, some sufficient conditions, expressed in terms of the probability generating function of Z1 and of its distribution function, are given under which a particular pair (α, U) is appropriate for (Zn). The most stringent set of conditions reduces, when U (x) x, to the requirements EZ1 = 1/α, EZ1 log Z1 <∞.

It is shown that the Wilks large sample likelihood ratio statistic λn, for testing between composite hypotheses Θ0 ⊂ Θ1 on the basis of a sample of size n, behaves as n varies like a diffusion process related to an equilibrium Ornstein-Uhlenbeck process, whenever the null hypothesis is true. This fact is used to construct large sample sequential tests based on λn, which are the same whatever the underlying distributions. In particular, the underlying distributions need not belong to an exponential family.

Atkinson and Reuter(1) consider travelling wave solutions for the deterministic epidemic, with or without removals, spreading along the line. In the case where there are no removals, they reformulate the problem in terms of the solutions X(·) to the integral equation

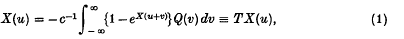
which satisfy X(− ∞) = − ∞, X( + ∞) = 0, X(u) < 0 for u ∈ (− ∞, ∞), where

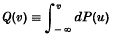
is the left hand tail of the contact distribution, and where ʗ > 0 is the velocity of the wave corresponding to X. They show that no solution is possible unless

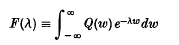
converges for λ > 0 sufficiently small, and that any solution X must satisfy

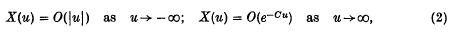
for some C > 0. They then prove the following existence theorems.

In a recent article, Kelly [4] has been able to exhibit interesting equilibrium properties for a wide class of ‘quasi-reversible’ queue networks. The assumption of quasi-reversibility puts restrictions on queue discipline, but not on the distributions of the service requirements of customers: however, because of the method of proof he employed, Kelly was forced to impose the condition that the service requirements were finite mixtures of gamma distributions. The form of the results he obtained led him to conjecture that this condition was in fact unnecessary, as is shown to be the case in this paper. The method used to prove the conjecture is of potentially wide application, in problems where the ‘method of stages' leads to useful simplification.

One way of analysing complicated Markov population processes is to approximate them by a diffusion about the deterministic path. This approximation alone may not, however, answer all the questions which might reasonably be asked. Many processes have phases, for example near boundaries, where a different approximation is required; such processes are better described by a succession of diffusion and special approximations alternately.

This paper looks at the special treatment required near a point where the deterministic equations are in equilibrium. When the equilibrium is unstable, the process will eventually wander off, and possibly follow a diffusion around another deterministic path. If the equilibrium is stable, the process will behave as if in stable equilibrium about it for a very much longer time, but may at last be trapped away from it, for instance in an absorbing state. The results presented describe the distributions of the time and place of leaving neighbourhoods of the equilibrium point. The neighbourhoods considered are large enough, in the unstable case, to make possible the link with the next phase of motion. In the stable case, exit times are shown to be so long that the possibility of exit can often be ignored in practice, and the quasi-equilibrium distribution treated as a true equilibrium. A more detailed result, showing how closely the normal approximation holds in this situation, is also provided.

Let X(t) be a continuous time Markov process on the integers such that, if σ is a time at which X makes a jump, X(σ)– X(σ–) is distributed independently of X(σ–), and has finite mean μ and variance. Let q(j) denote the residence time parameter for the state j. If tn denotes the time of the nth jump and X n ≡ X(t b ), it is easy to deduce limit theorems for from those for sums of independent identically distributed random variables. In this paper, it is shown how, for μ > 0 and for suitable q(·), these theorems can be translated into limit theorems for X(t), by using the continuous mapping theorem.

The paper examines those continuous time Markov processes Z(·) on the positive integers which have the ‘skip free upwards’ property, with regard to their asymptotic behaviour in the event of Z(t) tending to infinity. The behaviour is characterised in terms of the convergence or divergence of an appropriate function of Z(t), and the description is improved by central limit and iterated logarithm theorems. The conditions of the theorems are expressed entirely in terms of the matrix Q of instantaneous transition rates for Z(·). The method is applied, by way of example, to the super-critical linear birth and death process.

Let X1, X2, … be a sequence of independent random variables such that, for each n ≥ 1, EXn = 0 and and assume that then converges almost surely as N → ∞. Let and let Fn(x) denote the distribution function of Xn. Loynes (2) observed that the sequence {Sn} is a reversed martingale, and applied his central limit theorem to it: however, stronger results are obtainable, in precise duality with the classical theory of partial sums of independent random variables. These results describe the fluctuations of the sequence {Sn}, and hence the way in which converges to its limit.

Let {X N (t)} be a sequence of continuous time Markov population processes on an n-dimensional integer lattice, such that X N has initial state Nx(0) and has a finite number of possible transitions J from any state X: let the transition X → X + J have rate NgJ (N –1X), and let gJ (x) and x (0) be fixed as N varies. The rate of convergence of √N(N –1X N (t) — ζ (t)) to a Gaussian diffusion is investigated, where ζ(t) is the deterministic approximation to N –1XN (t), and a method of deriving higher order asymptotic expansions for its distribution is justified. The methods are applied to two birth and death processes, and to the closed stochastic epidemic.

Equations are derived describing a central limit type large population approximation for continuous time Markov lattice processes in one or more dimensions, such as are commonly encountered in biological models. A method of solving the equations using only the deterministic solution of the process is explained, and it is extended by the use of a martingale argument to provide more detailed information about the process.