Analytical expressions are derived for the velocity field, and effective slip lengths, associated with pressure-driven longitudinal flow in a circular superhydrophobic pipe whose boundary is patterned with a general arrangement of longitudinal no-shear stripes not necessarily possessing any rotational symmetry. First, the flow in a superhydrophobic pipe with 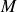$M$ different no-shear stripes in general position is found for 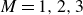$M=1, 2, 3$. The method, which is based on use of so-called prime functions, is such that with these cases covered, generalisation to any 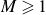$M \geqslant 1$ follows in a straightforward manner. It is shown how any one of these solutions can be generalised to solve for flow along superhydrophobic pipes where that pattern of 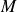$M$ menisci is repeated 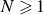$N \geqslant 1$ times around the boundary in a rotational symmetric arrangement. The work provides an extension of the canonical pipe flow solution for an 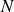$N$-fold rotationally symmetric pattern of no-shear stripes due to Philip (Angew. Math. Phys., vol. 23, 1972, pp. 353–372). The novel solution method, and the solutions that it produces, have significance for a wide range of mixed boundary value problems involving Poisson’s equation arising in other applications.

Analytical expressions for the velocity field and the effective slip length of pressure-driven Stokes flow through slippery pipes and annuli with rotationally symmetrical longitudinal slits are derived. Specifically, the developed models incorporate a finite local slip length and constant shear stress along the slits, and thus go beyond the assumption of perfect slip employed commonly for superhydrophobic surfaces. Thereby, they provide the possibility to assess the influence of both the viscosity of the air or other fluid that is modelled to fill the slits as well as the influence of the micro-geometry of these slits. First, expressions for tubes and annular pipes with superhydrophobic or slippery walls are provided. Second, these solutions are combined to a tube-within-a circular-pipe scenario, where one fluid domain provides a slip to the other. This scenario is interesting as an application to achieve stable fluid–fluid interfaces. With respect to modelling, it illustrates the specification of the local slip length depending on a linked flow field. The comparison of the analytically calculated solutions with numerical simulations shows excellent agreement. The results of this paper thus represent an important instrument for the design and optimization of slippage along surfaces in circular geometries.

We investigate theoretically, on the basis of the steady Stokes equations for a viscous incompressible fluid, the flow induced by a stokeslet located on the centre axis of two coaxially positioned rigid disks. The stokeslet is directed along the centre axis. No-slip boundary conditions are assumed to hold at the surfaces of the disks. We perform the calculation of the associated Green's function in large parts analytically, reducing the spatial evaluation of the flow field to one-dimensional integrations amenable to numerical treatment. To this end, we formulate the solution of the hydrodynamic problem for the viscous flow surrounding the two disks as a mixed boundary-value problem, which we then reduce to a system of four dual integral equations. We show the existence of viscous toroidal eddies arising in the fluid domain bounded by the two disks, manifested in the plane containing the centre axis through adjacent counter-rotating eddies. Additionally, we probe the effect of the confining disks on the slow dynamics of a point-like particle by evaluating the hydrodynamic mobility function associated with axial motion. Thereupon, we assess the appropriateness of the commonly employed superposition approximation and discuss its validity and applicability as a function of the geometrical properties of the system. Additionally, we complement our semi-analytical approach by finite-element computer simulations, which reveals a good agreement. Our results may find applications in guiding the design of microparticle-based sensing devices and electrokinetic transport in small-scale capacitors.

Analytical expressions for the flow field as well as for the effective slip length of a shear flow over a surface with periodic rectangular grooves are derived. The primary fluid is in the Cassie state with the grooves being filled with a secondary immiscible fluid. The coupling of the two fluids is reflected in a locally varying slip distribution along the fluid–fluid interface, which models the effect of the secondary fluid on the outer flow. The obtained closed-form analytical expressions for the flow field and effective slip length of the primary fluid explicitly contain the influence of the viscosities of the two fluids as well as the magnitude of the local slip, which is a function of the surface geometry. They agree well with results from numerical computations of the full geometry. The analytical expressions allow an investigation of the influence of the viscous stresses inside the secondary fluid for arbitrary geometries of the rectangular grooves. For classic superhydrophobic surfaces, the deviations in the effective slip length compared to the case of inviscid gas flow are pointed out. Another important finding with respect to an accurate modelling of flow over microstructured surfaces is that not only the effective slip length, but also the local slip length of a grooved surface, is anisotropic.

An analytical solution for the low-Reynolds-number flow field of a shear flow over a rectangular cavity containing a second immiscible fluid is derived. While flow of a single-phase fluid over a cavity is a standard case investigated in fluid dynamics, flow over a cavity that is filled with a second immiscible fluid has received little attention. The flow field inside the cavity is considered to define a boundary condition for the outer flow, which takes the form of a Navier slip condition with locally varying slip length. The slip-length function is determined heuristically from the related problem of lid-driven cavity flow. Based on the Stokes equations and complex analysis, it is then possible to derive a closed analytical expression for the flow field over the cavity for both the transverse and the longitudinal case. The result is a comparatively simple function, which displays the dependence of the flow field on the cavity geometry and the medium filling the cavity. The analytically computed expression agrees well with results obtained from a numerical solution of the Navier–Stokes equations.