We report measurements of the temperature frequency spectra $P(\,f, z, r)$, the variance $\sigma ^2(z,r)$ and the Nusselt number $Nu$ in turbulent Rayleigh–Bénard convection (RBC) over the Rayleigh number range $4\times 10^{11} \underset{\smash{\scriptscriptstyle\thicksim}} { < } Ra \underset{\smash{\scriptscriptstyle\thicksim}} { < } 5\times 10^{15}$ and for a Prandtl number $Pr \simeq ~0.8$ ($z$ is the vertical distance from the bottom plate and $r$ is the radial position). Three RBC samples with diameter $D = 1.12$ m yet different aspect ratios $\varGamma \equiv D/L = 1.00$, $0.50$ and $0.33$ ($L$ is the sample height) were used. In each sample, the results for $\sigma ^2/\varDelta ^2$ ($\varDelta$ is the applied temperature difference) in the classical state over the range $0.018 \underset{\smash{\scriptscriptstyle\thicksim}} { < } z/L \underset{\smash{\scriptscriptstyle\thicksim}} { < } 0.5$ can be collapsed onto a single curve, independent of $Ra$, by normalizing the distance $z$ by the thermal boundary layer thickness $\lambda = L/(2 Nu)$. One can derive the equation $\sigma ^2/\varDelta ^2 = c_1\times \ln (z/\lambda )+c_2+c_3(z/\lambda )^{-0.5}$ from the observed $f^{-1}$ scaling of the temperature frequency spectrum. It fits the collapsed $\sigma ^2(z/\lambda )$ data in the classical state over the large range $20 \underset{\smash{\scriptscriptstyle\thicksim}} { < } z/\lambda \underset{\smash{\scriptscriptstyle\thicksim}} { < } 10^4$. In the ultimate state ($Ra \underset{\smash{\scriptscriptstyle\thicksim}} { > } Ra^*_2$) the data can be collapsed only when an adjustable parameter $\tilde \lambda = L/(2 \widetilde {Nu})$ is used to replace $\lambda$. The values of $\widetilde {Nu}$ are larger by about 10 % than the experimentally measured $Nu$ but follow the predicted $Ra$ dependence of $Nu$ for the ultimate RBC regime. The data for both the global heat transport and the local temperature fluctuations reveal the ultimate-state transitions at $Ra^*_2(\varGamma )$. They yield $Ra^*_2 \propto \varGamma ^{-3.0}$ in the studied $\varGamma$ range.

We report on turbulent thermal convection experiments in a rotating cylinder with a diameter ($D$) to height ($H$) aspect ratio of $\varGamma =D/H=0.5$. Using nitrogen and pressurised sulphur hexafluoride we cover Rayleigh numbers (Ra) from $8\times 10^{9}$ to $8\times 10^{14}$ at Prandtl numbers $0.72\lesssim {\textit {Pr}}\lesssim 0.94$. For these Ra we measure the global vertical heat flux (i.e. the Nusselt number – Nu), as well as statistical quantities of local temperature measurements, as a function of the rotation rate, i.e. the inverse Rossby number – 1/Ro. In contrast to measurements in fluids with a higher Pr we do not find a heat transport enhancement, but only a decrease of Nu with increasing 1/Ro. When normalised with Nu(0) for the non-rotating system, data for all different Ra collapse and, for sufficiently large 1/Ro, follow a power law ${\textit {Nu}}/{\textit {Nu}}_0\propto (1/{\textit {Ro}})^{-0.43}$. Furthermore, we find that both the heat transport and the temperature field qualitatively change at rotation rates $1/{\textit {Ro}}^*_1=0.8$ and $1/{\textit {Ro}}^*_2=4$. We interpret the first transition at $1/{\textit {Ro}}^*_1$ as change from a large-scale circulation roll to the recently discovered boundary zonal flow (BZF). The second transition at rotation rate $1/{\textit {Ro}}^*_2$ is not associated with a change of the flow morphology, but is rather the rotation rate for which the BZF is at its maximum. For faster rotation the vertical transport of warm and cold fluid near the sidewall within the BZF decreases and hence so does Nu.

A detailed assessment of the inter-scale energy budget of the turbulent flow in a von Kármán mixing tank has been performed based on two extensive experimental data sets. Measurements were performed at a Taylor microscale Reynolds number of $Re_{\unicode[STIX]{x1D706}}=199$ in the central region of the tank, using scanning particle image velocimetry (PIV) to fully resolve the velocity gradient tensor (VGT), and stereoscopic PIV for an expanded field of view. Following a basic flow characterisation, the Kármán–Howarth–Monin–Hill equation was used to investigate the inter-scale energy transfer. Access to the full VGT enabled the contribution of the different terms of the energy budget to be evaluated without any assumptions or approximations. The scale-space distribution of the dominant terms was also reported to assess the isotropy of the energy transfer. The results show a highly anisotropic distribution of energy transfer in scale space. Energy transfer was shown in a spherically averaged sense to be dominated at the small scales by the nonlinear inter-scale transfer term. However, in contrast to flows considered in previous studies, the local energy transfer is found to depend heavily on the linear contribution associated with the mean flow. Analysis of the scale-to-scale transfer of energy also allowed direct assessment of the classical picture of the energy cascade. It was found that while the inter-scale energy cascade driven by the turbulent fluctuations always proceeds in the forward direction, the total energy cascade driven by both the turbulent fluctuations and the mean flow exhibits significant inverse cascade regions, where energy is transferred from smaller to larger scales.

We critically analyse the different ways to evaluate the dependence of the Nusselt number ($\mathit{Nu}$) on the Rayleigh number ($\mathit{Ra}$) in measurements of the heat transport in turbulent Rayleigh–Bénard convection under general non-Oberbeck–Boussinesq conditions and show the sensitivity of this dependence to the choice of the reference temperature at which the fluid properties are evaluated. For the case when the fluid properties depend significantly on the temperature and any pressure dependence is insignificant we propose a method to estimate the centre temperature. The theoretical predictions show very good agreement with the Göttingen measurements by He et al. (New J. Phys., vol. 14, 2012, 063030). We further show too the values of the normalized heat transport $\mathit{Nu}/\mathit{Ra}^{1/3}$ are independent of whether they are evaluated in the whole convection cell or in the lower or upper part of the cell if the correct reference temperatures are used.

This paper reports on a theoretical analysis of the rich variety of spatio-temporal patterns observed recently in inclined layer convection at medium Prandtl number when varying the inclination angle ${\it\gamma}$ and the Rayleigh number $R$ . The present numerical investigation of the inclined layer convection system is based on the standard Oberbeck–Boussinesq equations. The patterns are shown to originate from a complicated competition of buoyancy driven and shear-flow driven pattern forming mechanisms. The former are expressed as longitudinal convection rolls with their axes oriented parallel to the incline, the latter as perpendicular transverse rolls. Along with conventional methods to study roll patterns and their stability, we employ direct numerical simulations in large spatial domains, comparable with the experimental ones. As a result, we determine the phase diagram of the characteristic complex 3-D convection patterns above onset of convection in the ${\it\gamma}{-}R$ plane, and find that it compares very well with the experiments. In particular we demonstrate that interactions of specific Fourier modes, characterized by a resonant interaction of their wavevectors in the layer plane, are key to understanding the pattern morphologies.

We present measurements of the orientation ${\it\theta}_{0}$ and temperature amplitude ${\it\delta}$ of the large-scale circulation in a cylindrical sample of turbulent Rayleigh–Bénard convection (RBC) with aspect ratio ${\it\Gamma}\equiv D/L=1.00$ ( $D$ and $L$ are the diameter and height respectively) and for the Prandtl number $Pr\simeq 0.8$ . The results for ${\it\theta}_{0}$ revealed a preferred orientation with up-flow in the west, consistent with a broken azimuthal invariance due to the Earth’s Coriolis force (see Brown & Ahlers (Phys. Fluids, vol. 18, 2006, 125108)). They yielded the azimuthal diffusivity $D_{{\it\theta}}$ and a corresponding Reynolds number $Re_{{\it\theta}}$ for Rayleigh numbers over the range $2\times 10^{12}\lesssim Ra\lesssim 1.5\times 10^{14}$ . In the classical state ( $Ra\lesssim 2\times 10^{13}$ ) the results were consistent with the measurements by Brown & Ahlers (J. Fluid Mech., vol. 568, 2006, pp. 351–386) for $Ra\lesssim 10^{11}$ and $Pr=4.38$ , which gave $Re_{{\it\theta}}\propto Ra^{0.28}$ , and with the Prandtl-number dependence $Re_{{\it\theta}}\propto Pr^{-1.2}$ as found previously also for the velocity-fluctuation Reynolds number $Re_{V}$ (He et al., New J. Phys., vol. 17, 2015, 063028). At larger $Ra$ the data for $Re_{{\it\theta}}(Ra)$ revealed a transition to a new state, known as the ‘ultimate’ state, which was first seen in the Nusselt number $Nu(Ra)$ and in $Re_{V}(Ra)$ at $Ra_{1}^{\ast }\simeq 2\times 10^{13}$ and $Ra_{2}^{\ast }\simeq 8\times 10^{13}$ . In the ultimate state we found $Re_{{\it\theta}}\propto Ra^{0.40\pm 0.03}$ . Recently, Skrbek & Urban (J. Fluid Mech., vol. 785, 2015, pp. 270–282) claimed that non-Oberbeck–Boussinesq effects on the Nusselt and Reynolds numbers of turbulent RBC may have been interpreted erroneously as a transition to a new state. We demonstrate that their reasoning is incorrect and that the transition observed in the Göttingen experiments and discussed in the present paper is indeed to a new state of RBC referred to as ‘ultimate’.

We report on experimental determinations of the temperature field in the interior (bulk) of turbulent Rayleigh–Bénard convection for a cylindrical sample with an aspect ratio (diameter 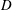$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}D$ over height  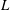$L$ ) equal to 0.50, in both the classical and the ultimate state. The measurements are for Rayleigh numbers 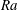$\mathit{Ra}$ from 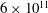$6\times 10^{11}$ to 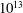$10^{13}$ in the classical and 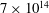$7\times 10^{14}$ to 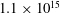$1.1\times 10^{15}$ (our maximum accessible 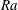$\mathit{Ra}$ ) in the ultimate state. The Prandtl number was close to 0.8. Although to lowest order the bulk is often assumed to be isothermal in the time average, we found a‘logarithmic layer’ (as reported briefly by Ahlers et al., Phys. Rev. Lett., vol. 109, 2012, 114501) in which the reduced temperature 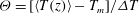$\varTheta = [\langle T(z) \rangle - T_m]/\Delta T$ (with 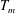$T_m$ the mean temperature, 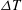$\Delta T$ the applied temperature difference and 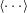$\langle {\cdots } \rangle $ a time average) varies as 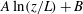$A \ln (z/L) + B$ or 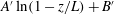$A^{\prime } \ln (1-z/L) + B^{\prime }$ with the distance $z$ from the bottom plate of the sample. In the classical state, the amplitudes 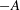$-A$ and 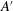$A^{\prime }$ are equal within our resolution, while in the ultimate state there is a small difference, with 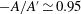$-A/A^{\prime } \simeq 0.95$ . For the classical state, the width of the log layer is approximately 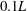$0.1L$ , the same near the top and the bottom plate as expected for a system with reflection symmetry about its horizontal midplane. For the ultimate state, the log-layer width is larger, extending through most of the sample, and slightly asymmetric about the midplane. Both amplitudes 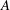$A$ and 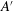$A^{\prime }$ vary with radial position $r$ , and this variation can be described well by 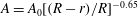$A = A_0 [(R - r)/R]^{-0.65}$ , where 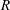$R$ is the radius of the sample. In the classical state, these results are in good agreement with direct numerical simulations (DNS) for 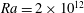$\mathit{Ra} = 2\times 10^{12}$ ; in the ultimate state there are as yet no DNS. The amplitudes 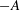$-A$ and 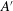$A^{\prime }$ varied as 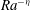${\mathit{Ra}}^{-\eta }$ , with 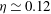$\eta \simeq 0.12$ in the classical and 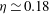$\eta \simeq 0.18$ in the ultimate state. A close analogy between the temperature field in the classical state and the ‘law of the wall’ for the time-averaged downstream velocity in shear flow is discussed. 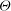A two-sublayer mean-field model of the temperature profile in the classical state was analysed and yielded a logarithmic $z$ dependence of $\varTheta $ . The 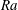$\mathit{Ra}$ dependence of the amplitude 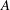$A$ given by the model corresponds to an exponent 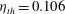$\eta _{th} = 0.106$ , in good agreement with the experiment. In the ultimate state the experimental result 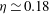$\eta \simeq 0.18$ differs from the prediction 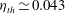$\eta _{th} \simeq 0.043$ by Grossmann & Lohse (Phys. Fluids, vol. 24, 2012, 125103).

We report experimental results on the dynamics of heavy particles of the size of the Kolmogorov scale in a fully developed turbulent flow. The mixed Eulerian structure function of two-particle velocity and acceleration difference vectors was observed to increase significantly with particle inertia for identical flow conditions. We show that this increase is related to a preferential alignment between these dynamical quantities. With increasing particle density the probability for those two vectors to be collinear was observed to grow. We show that these results are consistent with the preferential sampling of strain-dominated regions by inertial particles.

We ask whether the scaling exponents or the Kolmogorov constants depend on the anisotropy of the velocity fluctuations in a turbulent flow with no shear. According to our experiment, the answer is no for the Eulerian second-order transverse velocity structure function. The experiment consisted of 32 loudspeaker-driven jets pointed toward the centre of a spherical chamber. We generated anisotropy by controlling the strengths of the jets. We found that the form of the anisotropy of the velocity fluctuations was the same as that in the strength of the jets. We then varied the anisotropy, as measured by the ratio of axial to radial root-mean-square (r.m.s.) velocity fluctuations, between 0.6 and 2.3. The Reynolds number was approximately constant at around . In a central volume with a radius of 50 mm, the turbulence was approximately homogeneous, axisymmetric, and had no shear and no mean flow. We observed that the scaling exponent of the structure function was , independent of the anisotropy and regardless of the direction in which we measured it. The Kolmogorov constant, , was also independent of direction and anisotropy to within the experimental error of 4 %.

For the Rayleigh-number range 107 ≲ Ra ≲ 1011 we report measurements of the Nusselt number Nu and of properties of the large-scale circulation (LSC) for cylindrical samples of helium gas (Prandtl number Pr = 0.674) that have aspect ratio Γ ≡ D/L = 0.50 (D and L are the diameter and the height respectively) and are heated from below. The results for Nu are consistent with recent direct numerical simulations. We measured the amplitude δ of the azimuthal temperature variation induced by the LSC at the sidewall, and the LSC circulation-plane orientation θ0, at three vertical positions. For the entire Ra range the LSC involves a convection roll that is coherent over the height of the system. However, this structure frequently collapses completely at irregular time intervals and then reorganizes from the incoherent flow. At small δ the probability distribution p(δ) increases linearly from zero; for Γ = 1 and Pr = 4.38 this increase is exponential. No evidence of a two-roll structure, with one above the other, was observed. This differs from recent direct numerical simulations for Γ = 0.5 and Pr = 0.7, where a one-roll LSC was found to exist only for Ra ≲ 109 to 1010, and from measurements for Γ = 0.5 and Pr ≃ 5, where one- and two-roll structures were observed with transitions between them at random time intervals.

By tracking small particles in the bulk of an intensely turbulent laboratory flow, we study the effect of long-chain polymers on the Eulerian structure functions. We find that the structure functions are modified over a wide range of length scales even for very small polymer concentrations. Their behaviour can be captured by defining a length scale that depends on the solvent viscosity, the polymer relaxation time and the Weissenberg number. This result is not captured by current models. Additionally, the effects we observe depend strongly on the concentration. While the dissipation-range statistics change smoothly as a function of polymer concentration, we find that the inertial-range values of the structure functions are modified only when the concentration exceeds a threshold of approximately 5 parts per million (p.p.m.) by weight for the 18 × 106 atomic mass unit (a.m.u.) molecular weight polyacrylamide used in the experiment.

Experimental and theoretical investigations of undulation patterns in high-pressure inclined layer gas convection at a Prandtl number near unity are reported. Particular focus is given to the competition between the spatiotemporal chaotic state of undulation chaos and stationary patterns of ordered undulations. In experiments, a competition and bistability between the two states is observed, with ordered undulations most prevalent at higher Rayleigh number. The spectral pattern entropy, spatial correlation lengths and defect statistics are used to characterize the competing states. The experiments are complemented by a theoretical analysis of the Oberbeck–Boussinesq equations. The stability region of the ordered undulations as a function of their wave vectors and the Rayleigh number is obtained with Galerkin techniques. In addition, direct numerical simulations are used to investigate the spatiotemporal dynamics. In the simulations, both ordered undulations and undulation chaos were observed dependent on initial conditions. Experiment and theory are found to agree well.

We use silicon strip detectors (originally developed for the CLEO III high-energy particle physics experiment) to measure fluid particle trajectories in turbulence with temporal resolution of up to 70000 frames per second. This high frame rate allows the Kolmogorov time scale of a turbulent water flow to be fully resolved for 140 [ges ] Rλ [ges ] 970. Particle trajectories exhibiting accelerations up to 16000 m s−2 (40times the r.m.s. value) are routinely observed. The probability density function of the acceleration is found to have Reynolds-number-dependent stretched exponential tails. The moments of the acceleration distribution are calculated. The scaling of the acceleration component variance with the energy dissipation is found to be consistent with the results for low-Reynolds-number direct numerical simulations, and with the K41-based Heisenberg–Yaglom prediction for Rλ [ges ] 500. The acceleration flatness is found to increase with Reynolds number, and to exceed 60 at Rλ = 970. The coupling of the acceleration to the large-scale anisotropy is found to be large at low Reynolds number and to decrease as the Reynolds number increases, but to persist at all Reynolds numbers measured. The dependence of the acceleration variance on the size and density of the tracer particles is measured. The autocorrelation function of an acceleration component is measured, and is found to scale with the Kolmogorov time τη.

The directional solidification of the transparent binary alloy succinonitrile-poly(ethylene oxide) was studied in an experiment in which solidification speeds of about 2 mm/sec could be reached without loss of the linear temperature gradient. The low diffusivity of the polymer solute allowed the study of the dynamics of rapid solidification using an optical microscope. For both normal and doublonic dendrites we observed a transition to large triangular “superdendrites” above a certain solidification speed and we report measurements of the primary and secondary spacing as a function of the pulling speed. Our measurements suggest that the observed triangular shape is due to a decoupling of primary and secondary growth at large undercooling.