We recall that a JC-algebra (Størmer (3)) is a norm closed Jordan algebra of self-adjoint operators on a Hilbert space. Recently, Alfsen, Shultz, and Størmer (1) have introduced a class of abstract normed Jordan algebras called JB-algebras, and have proved that every special JB-algebra is isometrically isomorphic to a JC-algebra. We show that this result brings to a satisfactory conclusion the discussion in (2) of certain wedges W in Banach algebras and their related Jordan algebras W–W, and leads to two characterisations of the bicontinuously isomorphic images of JC-algebras.

The Poisson kernel is defined for z in the open unit disc D and ζ in the unit circle ∂D. As usually employed, it is integrated with respect to the second variable and a measure on ∂D to yield a harmonic function on D. Here, we fix a σ-finite positive Borel measure m on D and integrate the Poisson kernel with respect to the first variable against a function φ in L1(m) to obtain a function Tmφ on ∂D. We ask for what measures m the range of Tm is L1(∂D), for what m the kernel of Tm is non-zero, and for what m every positive continuous function on ∂D is of the form Tmφ with φ non-negative. When m is the counting measure of a countably infinite subset {ak:k∈ℕ} of D, the function (Tmφ)(ζ) is of the form with . The main results generalize results previously obtained for sums of this form. A related mapping from Lp(m) into Lp(∂D) with 1 <p<∞ is briefly considered.

For z in D and ζ in ∂D, we denote by pz(ζ) the Poisson kernel (1 − │z│2)│1 − ζ−2 for the open unit disc D. We ask for what countable sets {an:n∈ℕ} of points of D there exist complex numbers λn with

by which we mean that the series converges to zero in the norm of L1(∂D).

For what sequences {an} of points of the open unit disc D does there exist a constant k such that

for all bounded harmonic functions f on D?

We prove that if t is a compact linear operator that is not quasi-nilpotent and is appropriately normalised, then the closed semi-algebra A(t) generated by t is locally compact. The theory of locally compact semi-algebras (2) is therefore applicable to A(t), and we show that it can be used to obtain spectral properties of t.

Let A denote a complex Banach algebra with unit, Inv(A) the set of invertible elements of A, Sp(a) and r(a) the spectrum and spectral radius respectively of an element a of A. Let Γ denote the set of elements of A whose spectra contain non-negative real numbers, i.e.

Ajdovska Jama (The Pagan's Cave) in southeast Slovenia lies within the catchment of the River Sava, a major tributary of the Danube. The site is well known for its Neolithic burials and has been excavated to a high standard on various occasions since 1884. The human remains at the site occurred as distinct clusters of mainly disarticulated bones belonging to at least 31 individuals. Hitherto, dating of the burials has been based on the associated archaeological finds, including a few low-precision radiometric radiocarbon measurements on charred plant material. In the present study, bones from 15 individuals were subsampled for accelerator mass spectrometry (AMS) and stable isotope analyses. These comprised adults and children from 3 of the clusters. The results of the study indicate that the burials all belong to a relatively short time interval, while the stable isotope data indicate a mixed diet based on C3 plant and animal food sources. These interpretations differ somewhat from those of previous researchers. The AMS 14C and stable isotope analyses form part of a wider investigation of dietary and demographic change from the Mesolithic to the Iron Age in the Danube Basin.

A previous radiocarbon dating and stable isotope study of directly associated ungulate and human bone samples from Late Mesolithic burials at Schela Cladovei in Romania established that there is a freshwater reservoir effect of approximately 500 yr in the Iron Gates reach of the Danube River valley in southeast Europe. Using the δ15N values as an indicator of the percentage of freshwater protein in the human diet, the 14C data for 24 skeletons from the site of Lepenski Vir were corrected for this reservoir effect. The results of the paired 14C and stable isotope measurements provide evidence of substantial dietary change over the period from about 9000 BP to about 300 BP. The data from the Early Mesolithic to the Chalcolithic are consistent with a 2-component dietary system, where the linear plot of isotopic values reflects mixing between the 2 end-members to differing degrees. Typically, the individuals of Mesolithic age have much heavier δ15N signals and slightly heavier δ13C, while individuals of Early Neolithic and Chalcolithic age have lighter δ15N and δ13C values. Contrary to our earlier suggestion, there is no evidence of a substantial population that had a transitional diet midway between those that were characteristic of the Mesolithic and Neolithic. However, several individuals with “Final Mesolithic” 14C ages show δ15N and δ13C values that are similar to the Neolithic dietary pattern. Provisionally, these are interpreted either as incomers who originated in early farming communities outside the Iron Gates region or as indigenous individuals representing the earliest Neolithic of the Iron Gates. The results from Roman and Medieval age burials show a deviation from the linear function, suggesting the presence of a new major dietary component containing isotopically heavier carbon. This is interpreted as a consequence of the introduction of millet into the human food chain.

A semi-algebra of continuous functions is a cone$A$ of continuous real functions on a compactHausdorff space $X$ such that $A$ contains the products of its elements. A cone $A$ is said to be of type $n$ if $f\in A$ implies$f^n(1 + f)^{-1} \in A$. Uniformly closedsemi-algebras of types 0 and 1 have long beencharacterized in a manner analogous to the Stone--Weierstrass theorem, but, except forthe case when $A$ is generated by a singlefunction, little has been known about type 2.Here, progress is reported on two problems.The first is the characterization of those continuous linear functionals on $C(X)$ that determine semi-algebras of type 2. The secondis the determination of the type of the tensorproduct of two type 1 semi-algebras. 1991 Mathematics Subject Classification: 46J10.

Peller [4, 5] has proved that a Hankel operator S on the Hardy space H2 is in the trace class if and only if with h analytic on the open unit disc Dand with its second derivative belonging to the Bergman space L1a. This theorem does not include an estimate for the trace class norm ∥S∥1, of the operator in terms of the symbol function. In fact it is clear that cannot give an estimate for since the first two terms in the coefficient sequence of the Hankel operator have been removed by differentiation.

We obtain an explicit formula for the essential norm of a Hankel operator with its symbol in the space PC, which is the closure in L∞ of the space of piecewise continuous functions on the unit circle . It follows from this formula that functions in PC can be approximated as closely by functions in C, the continuous functions on the circle, as by functions in the much larger space H∞ + C. This is an example of the way in which properties of the Hardy spaces can be derived from properties of Hankel operators.

The Vidav–Palmer theorem [(11), (5), (2) (p. 65)] characterizes C*-algebras among Banach algebras in terms of the algebra and norm structure alone, without reference to an involution, in the following way. Let B denote a complex unital Banach algebra, and let Her (B) denote the set of Hermitian elements of B, that is the elements of B with real numerical ranges. In this notation, the Vidav–Palmer theorem tells us that if

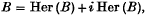
then B is isometrically isomorphic to a C*-algebra of operators on a Hilbert space, with the Hermitian elements corresponding to the self-adjoint operators in the C*-algebra.

Let U be a unilateral shift of arbitrary (perhaps uncountable) multiplicity on a Hilbert space. Following Rosenblum (5), an operator A is said to be a Hankel operator relative to U if

Hartman (2) has characterized the compact Hankel operators relative to the unilateral shift of multiplicity one as the Hankel operators with symbol in H∞ + C(T). Using the usual function space model for representing the unilateral shift, Page ((4), theorem 10) has extended Hartman's theorem to unilateral shifts of countable multiplicity. We give a model-free proof of Hartman's theorem which applies to shifts of arbitrary multiplicity. The proof turns on the observation that a compact operator acts compactly on a certain algebra of operators.