A simple probabilistic argument shows that every r-uniform hypergraph with m edges contains an r-partite subhypergraph with at least $({r!}/{r^r})m$ edges. The celebrated result of Edwards states that in the case of graphs, that is $r=2$, the resulting bound $m/2$ can be improved to $m/2+\Omega(m^{1/2})$, and this is sharp. We prove that if $r\geq 3$, then there is an r-partite subhypergraph with at least $({r!}/{r^r}) m+m^{3/5-o(1)}$ edges. Moreover, if the hypergraph is linear, this can be improved to $({r!}/{r^r}) m+m^{3/4-o(1)}$, which is tight up to the o(1) term. These improve results of Conlon, Fox, Kwan and Sudakov. Our proof is based on a combination of probabilistic, combinatorial, and linear algebraic techniques, and semidefinite programming.

A key part of our argument is relating the energy $\mathcal{E}(G)$ of a graph G (i.e. the sum of absolute values of eigenvalues of the adjacency matrix) to its maximum cut. We prove that every m edge multigraph G has a cut of size at least $m/2+\Omega({\mathcal{E}(G)}/{\log m})$, which might be of independent interest.

One of the central questions in Ramsey theory asks how small the largest clique and independent set in a graph on N vertices can be. By the celebrated result of Erdős from 1947, a random graph on N vertices with edge probability 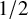$1/2$ contains no clique or independent set larger than 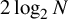$2\log _2 N$, with high probability. Finding explicit constructions of graphs with similar Ramsey-type properties is a famous open problem. A natural approach is to construct such graphs using algebraic tools.

Say that an r-uniform hypergraph 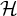$\mathcal {H}$ is algebraic of complexity 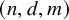$(n,d,m)$ if the vertices of 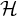$\mathcal {H}$ are elements of 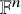$\mathbb {F}^{n}$ for some field 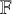$\mathbb {F}$, and there exist m polynomials 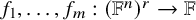$f_1,\dots ,f_m:(\mathbb {F}^{n})^{r}\rightarrow \mathbb {F}$ of degree at most d such that the edges of 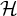$\mathcal {H}$ are determined by the zero-patterns of $f_1,\dots ,f_m$. The aim of this paper is to show that if an algebraic graph (or hypergraph) of complexity 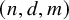$(n,d,m)$ has good Ramsey properties, then at least one of the parameters 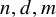$n,d,m$ must be large.

In 2001, Rónyai, Babai and Ganapathy considered the bipartite variant of the Ramsey problem and proved that if G is an algebraic graph of complexity 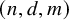$(n,d,m)$ on N vertices, then either G or its complement contains a complete balanced bipartite graph of size 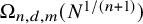$\Omega _{n,d,m}(N^{1/(n+1)})$. We extend this result by showing that such G contains either a clique or an independent set of size 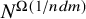$N^{\Omega (1/ndm)}$ and prove similar results for algebraic hypergraphs of constant complexity. We also obtain a polynomial regularity lemma for r-uniform algebraic hypergraphs that are defined by a single polynomial that might be of independent interest. Our proofs combine algebraic, geometric and combinatorial tools.

In this short note, we prove the following analog of the Kővári–Sós–Turán theorem for intersection graphs of boxes. If G is the intersection graph of n axis-parallel boxes in $${{\mathbb{R}}^d}$$ such that G contains no copy of Kt,t, then G has at most ctn( log n)2d+3 edges, where c = c(d)>0 only depends on d. Our proof is based on exploring connections between boxicity, separation dimension and poset dimension. Using this approach, we also show that a construction of Basit, Chernikov, Starchenko, Tao and Tran of K2,2-free incidence graphs of points and rectangles in the plane can be used to disprove a conjecture of Alon, Basavaraju, Chandran, Mathew and Rajendraprasad. We show that there exist graphs of separation dimension 4 having superlinear number of edges.

Several discrete geometry problems are equivalent to estimating the size of the largest homogeneous sets in graphs that happen to be the union of few comparability graphs. An important observation for such results is that if G is an n-vertex graph that is the union of r comparability (or more generally, perfect) graphs, then either G or its complement contains a clique of size $n^{1/(r+1)}$.

This bound is known to be tight for $r=1$. The question whether it is optimal for $r\ge 2$ was studied by Dumitrescu and Tóth. We prove that it is essentially best possible for $r=2$, as well: we introduce a probabilistic construction of two comparability graphs on n vertices, whose union contains no clique or independent set of size $n^{1/3+o(1)}$.

Using similar ideas, we can also construct a graph G that is the union of r comparability graphs, and neither G nor its complement contain a complete bipartite graph with parts of size $cn/{(log n)^r}$. With this, we improve a result of Fox and Pach.

Let hom(G) denote the size of the largest clique or independent set of a graph G. In 2007, Bukh and Sudakov proved that every n-vertex graph G with hom(G) = O(logn) contains an induced subgraph with Ω(n 1/2) distinct degrees, and raised the question of deciding whether an analogous result holds for every n-vertex graph G with hom(G) = O(nϵ ), where ϵ > 0 is a fixed constant. Here, we answer their question in the affirmative and show that every graph G on n vertices contains an induced subgraph with Ω((n/hom(G))1/2) distinct degrees. We also prove a stronger result for graphs with large cliques or independent sets and show, for any fixed k ∈ ℕ, that if an n-vertex graph G contains no induced subgraph with k distinct degrees, then hom(G)⩾n/(k − 1) − o(n); this bound is essentially best possible.