We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Electrophoresis of a tightly fitting sphere of radius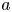 
$a$ along the centreline of a liquid-filled circular cylinder of radius 
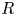$R$ is studied for a gap width 
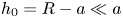$h_0=R-a\ll a$. We assume a Debye length 
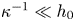$\kappa ^{-1}\ll h_0$, so that surface conductivity is negligible for zeta potentials typically seen in experiments, and the Smoluchowski slip velocity is imposed as a boundary condition at the solid surfaces. The pressure difference between the front and rear of the sphere is determined. If the cylinder has finite length 
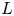$L$, this pressure difference causes an additional volumetric flow of liquid along the cylinder, increasing the electrophoretic velocity of the sphere, and an analytic prediction for this increase is found when 
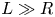$L\gg R$. If 
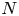$N$ identical, well-spaced spheres are present, the electrophoretic velocity of the spheres increases with 
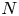$N$, in agreement with the experiments of Misiunas & Keyser (Phys. Rev. Lett., vol. 122, 2019, 214501).
