The classical Mordell–Weil theorem implies that an abelian variety A over a number field K has only finitely many K-rational torsion points. This finitude of torsion still holds even over the cyclotomic extension $K^{\mathrm {cyc}}=K{\mathbb Q}^{\mathrm {ab}}$ by a result of Ribet. In this article, we consider the finiteness of torsion points of an abelian variety A over the infinite algebraic extension $K_B$ obtained by adjoining the coordinates of all torsion points of an abelian variety B. Assuming the Mumford–Tate conjecture, and up to a finite extension of the base field K, we give a necessary and sufficient condition for the finiteness of $A(K_B)_{\mathrm tors}$ in terms of Mumford–Tate groups. We give a complete answer when both abelian varieties have dimension at most 3, or when both have complex multiplication.

For families of smooth complex projective varieties, we show that normal functions arising from algebraically trivial cycle classes are algebraic and defined over the field of definition of the family. In particular, the zero loci of those functions are algebraic and defined over such a field of definition. This proves a conjecture of Charles.

We show that the image of the Abel–Jacobi map admits functorially a model over the field of definition, with the property that the Abel–Jacobi map is equivariant with respect to this model. The cohomology of this abelian variety over the base field is isomorphic as a Galois representation to the deepest part of the coniveau filtration of the cohomology of the projective variety. Moreover, we show that this model over the base field is dominated by the Albanese variety of a product of components of the Hilbert scheme of the projective variety, and thus we answer a question of Mazur. We also recover a result of Deligne on complete intersections of Hodge level 1.

A conjecture of Orlov predicts that derived equivalent smooth projective varieties over a field have isomorphic Chow motives. The conjecture is known for curves, and was recently observed for surfaces by Huybrechts. In this paper we focus on threefolds over perfect fields, and unconditionally secure results, which are implied by Orlov's conjecture, concerning the geometric coniveau filtration, and abelian varieties attached to smooth projective varieties.

In this paper, motivated by a problem posed by Barry Mazur, we show that for smooth projective varieties over the rationals, the odd cohomology groups of degree less than or equal to the dimension can be modeled by the cohomology of an abelian variety, provided the geometric coniveau is maximal. This provides an affirmative answer to Mazur’s question for all uni-ruled threefolds, for instance. Concerning cohomology in degree three, we show that the image of the Abel–Jacobi map admits a distinguished model over the rationals.

We consider the distribution of $p$ -power group schemes among the torsion of abelian varieties over finite fields of characteristic $p$ , as follows. Fix natural numbers $g$ and $n$ , and let ${\it\xi}$ be a non-supersingular principally quasipolarized Barsotti–Tate group of level $n$ . We classify the $\mathbb{F}_{q}$ -rational forms ${\it\xi}^{{\it\alpha}}$ of ${\it\xi}$ . Among all principally polarized abelian varieties $X/\mathbb{F}_{q}$ of dimension $g$ with $X[p^{n}]_{\bar{\mathbb{F}}_{q}}\cong {\it\xi}_{\bar{\mathbb{F}}_{q}}$ , we compute the frequency with which $X[p^{n}]\cong {\it\xi}^{{\it\alpha}}$ . The error in our estimate is bounded by $D/\sqrt{q}$ , where $D$ depends on $g$ , $n$ , and $p$ , but not on ${\it\xi}$ .

Consider a finite morphism 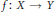$f\,:\,X\,\to \,Y$ of smooth, projective varieties over a finite field 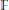$\mathbb{F}$ . Suppose 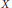$X$ is the vanishing locus in 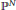${{\mathbb{P}}^{N}}$ of $r$ forms of degree at most $d$ . We show that there is a constant $C$ depending only on 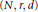$(N,\,r,\,d)$ and 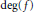$\deg (f)$ such that if 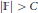$\left| \mathbb{F} \right|\,>\,C$ , then 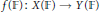$f\,(\mathbb{F})\,:\,X(\mathbb{F})\,\to Y(\mathbb{F})$ is injective if and only if it is surjective.