Leading-edge-vortex (LEV) formation often characterizes the unsteady flows past airfoils and wings. Recent research showed that initiation of LEV formation on airfoils in two-dimensional flow is closely tied to the criticality of the so-called leading-edge suction parameter (LESP). To characterize the LEV initiation on wings in three-dimensional flow, a large set of pitching wings was studied using Reynolds-averaged Navier–Stokes computations (computational fluid dynamics, CFD). The CFD results showed that the pitch angle and spanwise location for LEV initiation varied widely between the different wings. The same cases were also analysed using an unsteady vortex-lattice method (UVLM), which assumes attached flow. Low-order prediction of LEV initiation is assumed to occur at the pitch angle when the UVLM-calculated LESP at any point on the wing span first becomes equal to the pre-determined critical LESP for the airfoil. For all the cases, the predicted pitch angles and spanwise locations for LEV initiation from the low-order method agreed excellently with the corresponding CFD predictions. These observations show that LEV initiation on finite wings is governed by criticality of leading-edge suction, enabling the prediction of LEV initiation on an unsteady finite wing using attached-flow wing theory and the critical LESP values for the airfoil sections.

The suction force at the leading edge of a round-nosed aerofoil is an important indicator of the state of the flow over the leading edge and, often, the entire aerofoil. The leading-edge suction parameter (LESP) is a non-dimensional version of this force. In recent works, the LESP was calculated with good accuracy for attached flows at low Reynolds numbers (10 000–100 000) from unsteady aerofoil theory. In contrast to this ‘inviscid’ LESP, results from viscous computations and experiments are used here to calculate the ‘viscous’ LESP on aerofoils undergoing pitching motions at low subsonic speeds. The LESP formulation is also updated to account for the net velocity of the aerofoil. Spanning multiple aerofoils, Reynolds numbers and kinematics, the cases include motions in which dynamic stall occurs with or without leading-edge vortex (LEV) formation. Inflections in the surface pressure and skin-friction distributions near the leading edge are shown to be reliable indicators of LEV initiation. Critical LESP, which is the LESP value at LEV initiation, was found to be nearly independent of pivot location, weakly dependent on pitch rate and strongly dependent on Reynolds number. The viscous LESP was seen to drop to near-zero values when the flow is separated at the leading edge, irrespective of LEV formation. This behaviour was shown to correlate well with the loss of streamline curvature at the leading edge due to flow separation. These findings serve to improve our understanding and extend the applicability of the leading-edge suction behaviour gained from earlier works.

Full thickness rotator cuff tears (RCT) and the associated muscle degeneration that results due to this injury presents a significant clinical burden. The prevention or recovery from this degeneration requires the synchronized behavior of many cells that participate in regeneration. Strategies that tune the inflammatory cascade that is initiated after injury serves as a powerful way to influence tissue repair. Here, we use the local, sustained delivery of the immunomodulatory small molecule FTY720 to examine whether the recruitment of pro-regenerative myeloid cells affects the healing outcome. We find that PLGA microparticles have an atrophic effect on the muscle that is ameliorated with the release of FTY720. However, the inability of FTY720 delivery to induce pro-regenerative monocyte and macrophage recruitment and our findings demonstrating enrichment of CD4+ T cells suggest that effects of this small molecule are context dependent and that the underlying mechanisms behind this RCT associated muscle degeneration require further studies.

Unsteady aerofoil flows are often characterized by leading-edge vortex (LEV) shedding. While experiments and high-order computations have contributed to our understanding of these flows, fast low-order methods are needed for engineering tasks. Classical unsteady aerofoil theories are limited to small amplitudes and attached leading-edge flows. Discrete-vortex methods that model vortex shedding from leading edges assume continuous shedding, valid only for sharp leading edges, or shedding governed by ad-hoc criteria such as a critical angle of attack, valid only for a restricted set of kinematics. We present a criterion for intermittent vortex shedding from rounded leading edges that is governed by a maximum allowable leading-edge suction. We show that, when using unsteady thin aerofoil theory, this leading-edge suction parameter (LESP) is related to the 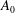$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}A_0$ term in the Fourier series representing the chordwise variation of bound vorticity. Furthermore, for any aerofoil and Reynolds number, there is a critical value of the LESP, which is independent of the motion kinematics. When the instantaneous LESP value exceeds the critical value, vortex shedding occurs at the leading edge. We have augmented a discrete-time, arbitrary-motion, unsteady thin aerofoil theory with discrete-vortex shedding from the leading edge governed by the instantaneous LESP. Thus, the use of a single empirical parameter, the critical-LESP value, allows us to determine the onset, growth, and termination of LEVs. We show, by comparison with experimental and computational results for several aerofoils, motions and Reynolds numbers, that this computationally inexpensive method is successful in predicting the complex flows and forces resulting from intermittent LEV shedding, thus validating the LESP concept.