We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we consider the beta(2 − α, α)-coalescents with 1 < α < 2 and study the moments of external branches, in particular, the total external branch length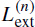 
of an initial sample of n individuals. For this class of coalescents, it has been proved that n α-1 T (n) →DT, where T (n) is the length of an external branch chosen at random and T is a known nonnegative random variable. For beta(2 − α, α)-coalescents with 1 < α < 2, we obtain limn→+∞ n 3α-5 𝔼(L ext (n) − n 2-α𝔼T)2 = ((α − 1)Γ(α + 1))2Γ(4 − α) / ((3 − α)Γ(4 − 2α)).
