We investigate nonlinear energy transfer for channel flows at friction Reynolds numbers 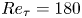$Re_{\tau }=180$ and 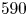$590$. The key feature of the analysis is that we quantify the energy transferred from a source mode to a recipient mode, with each mode characterised by a streamwise wavenumber and a spanwise wavenumber. This is achieved through an explicit examination of the triadic interactions of the nonlinear energy transfer term in the spectral turbulent kinetic energy equation. First, we quantify the nonlinear energy transfer gain and loss for individual Fourier modes. The gain and loss cannot be obtained without expanding the nonlinear triadic interactions. Second, we quantify the nonlinear energy transfer budgets for three types of modes. Each type of mode is characterised by a specific region in streamwise–spanwise wavenumber space. We find that a transverse cascade from streamwise-elongated modes to spanwise-elongated modes exists for all three types of modes. Third, we quantify the forward and inverse cascades between resolved scales and subgrid scales in the spirit of large-eddy simulations. For the cutoff wavelength range that we consider, the forward and inverse cascades between the resolved scales and subgrid scales result in a net forward cascade from the resolved scales to the subgrid scales. The shape of the net forward cascade curve with respect to the cutoff wavelength resembles the net forward cascade predicted by the Smagorinsky eddy viscosity.