A group G is termed conjugacy separable (c.s.) if any pair of distinct conjugacy classes may be mapped to distinct conjugacy classes in some finite epimorph of G. The free product of A and B with cyclic amalgamated subgroup H is shown to be c.s. if A and B are both free, or are both finitely generated nilpotent groups. Further, one-relator groups with nontrivial center and HNN extensions with c.s. base group and finite associated subgroups are also c.s.

In this paper we prove that the automorphism group A(N) of a free nilpotent group N of class 2 and finite rank n is complete, except when n is 1 or 3. Equivalently, the centre of A(N) is trivial and every automorphism of A(N) is inner, provided n ≠ 1 or 3. When n = 3, A(N) has an our automorphism of order 2, so A(A(N)) is a split extension of A(N) by 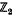. In this case, A(A(N)) is complete. These results provide some evidence supporting a conjecture of Gilbert Baumslag that the sequence

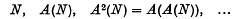
becomes periodic if N is a finitely generated nilpotent group.

Let R be a normal subgroup of the free group F, and set G = F/[R, R]. We assume that F/R is a torsion-free group which is either solvable and not cyclic, or has a non-trivial center and is not cyclic-by-periodic. Then any automorphism of G whose restriction to R/[R, R] is trivial is an inner automorphism, determined by some element of R/[R, R]. This result extends a theorem of Šmel'kin (1967).