In this article, we provide sufficient conditions on a self-similar interval exchange map, whose renormalization matrix has complex eigenvalues of modulus greater than one, for the existence of affine interval exchange maps with wandering intervals that are semi-conjugate with it. These conditions are based on the algebraic properties of the complex eigenvalues and the complex fractals built from the natural substitution emerging from self-similarity. We show that the cubic Arnoux–Yoccoz interval exchange map satisfies these conditions.

Let 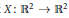$X:\,{{\mathbb{R}}^{2}}\to \,{{\mathbb{R}}^{2}}$ be a 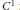${{C}^{1}}$ map. Denote by 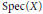$\text{Spec}(X)$ the set of (complex) eigenvalues of 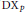$\text{D}{{\text{X}}_{p}}$ when 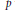$p$ varies in 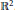${{\mathbb{R}}^{2}}$ . If there exists 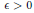$\in \,>\,0$ such that 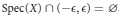$\text{Spec(}X)\,\bigcap \,(-\in ,\,\in )\,=\,\varnothing $ , then 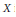$X$ is injective. Some applications of this result to the real Keller Jacobian conjecture are discussed.

If T is an interval exchange transformation we denote by C_{{\rm aff}}(T) (respectively S_{{\rm aff}}(T)) the set of piece-wise affine maps of the interval which are conjugate (respectively semi-conjugate) to T. In this work we will give a description of the set C_{{\rm aff}}(T) for almost allT. We present an explicit interval exchange T_0 such that S_{{\rm aff}}(T_0)\backslash C_{{\rm aff}}(T_0) is non-empty. All the elements of S_{{\rm aff}}(T_0)\backslash C_{{\rm aff}}(T_0) are uniquely ergodic and have a unique wandering interval.