We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We present a general approach to justify the random phase approximation for the homogeneous Fermi gas in three dimensions in the mean-field scaling regime. We consider a system of N fermions on a torus, interacting via a two-body repulsive potential proportional to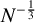 
$N^{-\frac {1}{3}}$. In the limit 
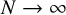$N\rightarrow \infty $, we derive the exact leading order of the correlation energy and the bosonic elementary excitations of the system, which are consistent with the prediction of the random phase approximation in the physics literature.
