We prove that complex Bernoulli convolutions are absolutely continuous in the supercritical parameter region, outside of an exceptional set of parameters of zero Hausdorff dimension. Similar results are also obtained in the biased case, and for other parametrised families of self-similar sets and measures in the complex plane, extending earlier results.

We consider the dimensions of a family of self-affine sets related to the Bedford–McMullen carpets. In particular, we fix a Bedford–McMullen system and then randomize the translation vectors with the stipulation that the column structure is preserved. As such, we maintain one of the key features in the Bedford–McMullen set-up in that alignment causes the dimensions to drop from the affinity dimension. We compute the Hausdorff, packing and box dimensions outside of a small set of exceptional translations, and also for some explicit translations even in the presence of overlapping. Our results rely on, and can be seen as a partial extension of, Hochman’s recent work on the dimensions of self-similar sets and measures.

We study dimensional properties of visible parts of fractal percolation in the plane. Provided that the dimension of the fractal percolation is at least 1, we show that, conditioned on non-extinction, almost surely all visible parts from lines are one dimensional. Furthermore, almost all of them have positive and finite Hausdorff measure. We also verify analogous results for visible parts from points. These results are motivated by an open problem on the dimensions of visible parts.

Let νpλ be the distribution of the random series 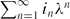, where in is a sequence of i.i.d. random variables taking the values 0, 1 with probabilities p, 1 − p. These measures are the well-known (biased) Bernoulli convolutions.

In this paper we study the multifractal spectrum of νpλ for typical λ. Namely, we investigate the size of the sets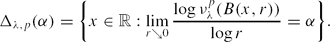Our main results highlight the fact that for almost all, and in some cases all, λ in an appropriate range, Δλ, p(α) is nonempty and, moreover, has positive Hausdorff dimension, for many values of α. This happens even in parameter regions for which νpλ is typically absolutely continuous.

We compute the Minkowski dimension for a family of self-affine sets on ℝ2. Our result holds for every (rather than generic) set in the class. Moreover, we exhibit explicit open subsets of this class where we allow overlapping, and do not impose any conditions on the norms of the linear maps. The family under consideration was inspired by the theory of Kakeya sets.

Let Ca be the central Cantor set obtained by removing a central interval of length 1−2a from the unit interval, and then continuing this process inductively on each of the remaining two intervals. We prove that if log b/log a is irrational, then where dimis Hausdorff dimension. More generally, given two self-similar sets K,K′ in ℝ and a scaling parameter s>0, if the dimension of the arithmetic sum K+sK′ is strictly smaller than dim (K)+dim (K′)≤1 (‘geometric resonance’), then there exists r<1 such that all contraction ratios of the similitudes defining K and K′ are powers of r (‘algebraic resonance’). Our method also yields a new result on the projections of planar self-similar sets generated by an iterated function system that includes a scaled irrational rotation.