For 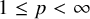 $1\le p <\infty $, we present a reflexive Banach space
$1\le p <\infty $, we present a reflexive Banach space 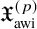 $\mathfrak {X}^{(p)}_{\text {awi}}$, with an unconditional basis, that admits
$\mathfrak {X}^{(p)}_{\text {awi}}$, with an unconditional basis, that admits 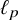 $\ell _p$ as a unique asymptotic model and does not contain any Asymptotic
$\ell _p$ as a unique asymptotic model and does not contain any Asymptotic 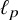 $\ell _p$ subspaces. Freeman et al., Trans. AMS. 370 (2018), 6933–6953 have shown that whenever a Banach space not containing
$\ell _p$ subspaces. Freeman et al., Trans. AMS. 370 (2018), 6933–6953 have shown that whenever a Banach space not containing 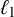 $\ell _1$, in particular a reflexive Banach space, admits
$\ell _1$, in particular a reflexive Banach space, admits 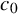 $c_0$ as a unique asymptotic model, then it is Asymptotic
$c_0$ as a unique asymptotic model, then it is Asymptotic 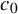 $c_0$. These results provide a complete answer to a problem posed by Halbeisen and Odell [Isr. J. Math. 139 (2004), 253–291] and also complete a line of inquiry of the relation between specific asymptotic structures in Banach spaces, initiated in a previous paper by the first and fourth authors. For the definition of
$c_0$. These results provide a complete answer to a problem posed by Halbeisen and Odell [Isr. J. Math. 139 (2004), 253–291] and also complete a line of inquiry of the relation between specific asymptotic structures in Banach spaces, initiated in a previous paper by the first and fourth authors. For the definition of 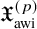 $\mathfrak {X}^{(p)}_{\text {awi}}$, we use saturation with asymptotically weakly incomparable constraints, a new method for defining a norm that remains small on a well-founded tree of vectors which penetrates any infinite dimensional closed subspace.
$\mathfrak {X}^{(p)}_{\text {awi}}$, we use saturation with asymptotically weakly incomparable constraints, a new method for defining a norm that remains small on a well-founded tree of vectors which penetrates any infinite dimensional closed subspace.
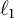 $\ell _{1}$ spreading models and the Lebesgue property of Banach spaces
$\ell _{1}$ spreading models and the Lebesgue property of Banach spaces
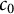 $c_0$ or
$c_0$ or 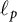 $ \ell _{p}$
$ \ell _{p}$
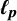 $\boldsymbol {\ell _{p}}$ structures for
$\boldsymbol {\ell _{p}}$ structures for 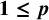 $ \boldsymbol {1\le p}$<
$ \boldsymbol {1\le p}$<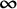 $ \boldsymbol {\infty }$
$ \boldsymbol {\infty }$
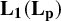 $\mathbf {L_1(L_p)}$ is primary for 1 < p < ∞
$\mathbf {L_1(L_p)}$ is primary for 1 < p < ∞
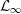 ${\mathcal{L}}_{\infty }$ -SPACES
${\mathcal{L}}_{\infty }$ -SPACES