We give an overview of irregular complex surfaces of general type, discussing in particular the distribution of the numerical invariants and for minimal ones.
1. Introduction
Let S be a minimal surface of general type and let be its main numerical invariants (Section 2.3). For every pair of positive integers a, b the surfaces with belong to finitely many irreducible families, so that in principle their classification is possible. In practice, the much weaker geographical problem, i.e., determining the pairs a, b for which there exists a minimal surface of general type with and, is quite hard.
In the past, the main focus in the study of both the geographical problem and the fine classification of surfaces of general type has been on regular surfaces, namely surfaces that have no global 1-forms, or, equivalently, whose first Betti number is 0. The reason for this is twofold: on the one hand, the canonical map of regular surfaces is easier to understand, on the other hand complex surfaces are the main source of examples of differentiable 4-manifolds, hence the simply connected ones are considered especially interesting from that point of view.
So, while, for instance, the geographical problem is by now almost settled and the fine classification of some families of regular surfaces is accomplished [Barth et al. 1984, §9-11, Chapter VII], little is known about irregular surfaces of general type. In recent years, however, the use of new methods and the revisiting of old ones have produced several new results.
Here we give an overview of these results, with special emphasis on the geographical problem. In addition, we give several examples and discuss some open questions and possible generalizations to higher dimensions (e.g., Theorem 5.2.2).
Notation and conventions. We work over the complex numbers. All varieties are projective algebraic and, unless otherwise specified, smooth. We denote by J(C) the Jacobian of a curve C.
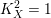 $K_{X}^{2}=1$
$K_{X}^{2}=1$