We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let X 1, X 2, …, X n be a sequence of independent, identically distributed positive integer random variables with distribution function F. Anderson (1970) proved a variant of the law of large numbers by showing that the sample maximum moves asymptotically on two values if and only if F satisfies a ‘clustering’ condition,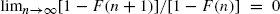 
In this article, we generalize Anderson's result and show that it is robust by proving that, for any r ≥ 0, the sample maximum and other extremes asymptotically cluster on r + 2 values if and only if 
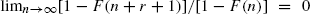Together with previous work which considered other asymptotic properties of these sample extremes, a more detailed asymptotic clustering structure for discrete order statistics is presented.
