We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this article, we investigate the topological structure of large-scale interacting systems on infinite graphs, by constructing a suitable cohomology which we call the uniform cohomology. The central idea for the construction is the introduction of a class of functions called uniform functions. Uniform cohomology provides a new perspective for the identification of macroscopic observables from the microscopic system. As a straightforward application of our theory when the underlying graph has a free action of a group, we prove a certain decomposition theorem for shift-invariant closed uniform forms. This result is a uniform version in a very general setting of the decomposition result for shift-invariant closed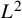 
$L^2$-forms originally proposed by Varadhan, which has repeatedly played a key role in the proof of the hydrodynamic limits of nongradient large-scale interacting systems. In a subsequent article, we use this result as a key to prove Varadhan’s decomposition theorem for a general class of large-scale interacting systems.
