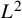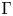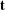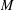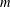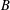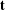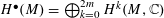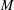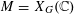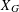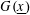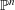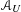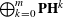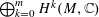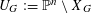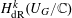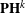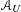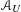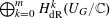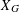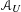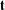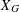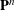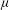In this article, we investigate the topological structure of large-scale interacting systems on infinite graphs, by constructing a suitable cohomology which we call the uniform cohomology. The central idea for the construction is the introduction of a class of functions called uniform functions. Uniform cohomology provides a new perspective for the identification of macroscopic observables from the microscopic system. As a straightforward application of our theory when the underlying graph has a free action of a group, we prove a certain decomposition theorem for shift-invariant closed uniform forms. This result is a uniform version in a very general setting of the decomposition result for shift-invariant closed $L^2$-forms originally proposed by Varadhan, which has repeatedly played a key role in the proof of the hydrodynamic limits of nongradient large-scale interacting systems. In a subsequent article, we use this result as a key to prove Varadhan’s decomposition theorem for a general class of large-scale interacting systems.

We analyse the $\Gamma$-convergence of general non-local convolution type functionals with varying densities depending on the space variable and on the symmetrized gradient. The limit is a local free-discontinuity functional, where the bulk term can be completely characterized in terms of an asymptotic cell formula. From that, we can deduce an homogenisation result in the stochastic setting.

Barannikov and Kontsevich [Frobenius manifolds and formality of Lie algebras of polyvector fields. Int. Math. Res. Not. IMRN1998(4) (1998), 201–215], constructed a DGBV (differential Gerstenhaber–Batalin–Vilkovisky) algebra 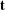$\mathbf{t}$ for a compact smooth Calabi–Yau complex manifold 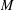$M$ of dimension 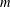$m$, which gives rise to the 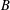$B$-side formal Frobenius manifold structure in the homological mirror symmetry conjecture. The cohomology of the DGBV algebra 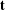$\mathbf{t}$ is isomorphic to the total singular cohomology 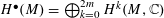$H^{\bullet }(M)=\bigoplus _{k=0}^{2m}H^{k}(M,\mathbb{C})$ of 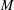$M$. If 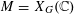$M=X_{G}(\mathbb{C})$, where 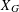$X_{G}$ is the hypersurface defined by a homogeneous polynomial 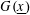$G(\text{}\underline{x})$ in the projective space 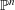$\mathbb{P}^{n}$, then we give a purely algorithmic construction of a DGBV algebra 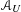${\mathcal{A}}_{U}$, which computes the primitive part 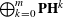$\bigoplus _{k=0}^{m}\mathbf{PH}^{k}$ of the middle-dimensional cohomology 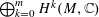$\bigoplus _{k=0}^{m}H^{k}(M,\mathbb{C})$, using the de Rham cohomology of the hypersurface complement 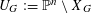$U_{G}:=\mathbb{P}^{n}\setminus X_{G}$ and the residue isomorphism from 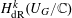$H_{\text{dR}}^{k}(U_{G}/\mathbb{C})$ to 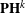$\mathbf{PH}^{k}$. We observe that the DGBV algebra 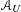${\mathcal{A}}_{U}$ still makes sense even for a singular projective Calabi–Yau hypersurface, i.e. 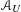${\mathcal{A}}_{U}$ computes 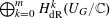$\bigoplus _{k=0}^{m}H_{\text{dR}}^{k}(U_{G}/\mathbb{C})$ even for a singular 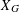$X_{G}$. Moreover, we give a precise relationship between 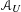${\mathcal{A}}_{U}$ and 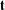$\mathbf{t}$ when 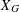$X_{G}$ is smooth in 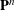$\mathbf{P}^{n}$.

Nanopore science, the study of individual nanoscale pores within thin membranes, is a fast-growing field which presents numerous interesting problems for physicists and applied mathematicians. Nanopores are most commonly applied to resistive pulse sensing (RPS) of individual particles suspended in aqueous electrolyte. The form of a resistive pulse is dependent on an array of experimental variables, including electrolyte characteristics, electrophoretic and convective transport, and (especially) pore and particle geometry. The level of analysis required depends on the application, but any broadly useful approach should be simple and flexible, due to the requirement for high data throughput and variations between different experimental systems and specimens. Here we review analytic methods for interpreting RPS experiments for particles in the approximate range 100 nm to 1 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mu $m, focusing on calculation of resistance change as a function of the particle’s position. We detail a recently developed semi-analytical model and compare the modelled electric field with finite element results. The model can also be used to calculate particle motion, so that the experimental current–time history can be reconstructed. This approach is useful for a wide range of pore and particle geometries, and includes consideration of entrance effects. Tunable elastomeric pores with truncated linear cone geometry are used as a model system.