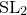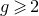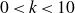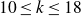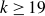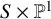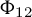Refine search
Actions for selected content:
9 results
K3 SURFACES AND ORTHOGONAL MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 29 August 2025, pp. 687-727
- Print publication:
- December 2025
-
- Article
- Export citation
Asymptotic Chow stability of symmetric reflexive toric varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On quasimap invariants of moduli spaces of Higgs bundles
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential forms on universal K3 surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 12 July 2024, pp. 1-9
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasimaps to moduli spaces of sheaves on a
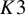 $K3$ surface
$K3$ surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 May 2024, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED AUTOMORPHIC SHEAVES AND THE PROPORTIONALITY PRINCIPLE OF HIRZEBRUCH-MUMFORD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 10 October 2023, pp. 1567-1605
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KODAIRA DIMENSION OF UNIVERSAL HOLOMORPHIC SYMPLECTIC VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 1849-1866
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Moduli of products of stable varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 06 September 2013, pp. 2036-2070
- Print publication:
- December 2013
-
- Article
- Export citation
Moduli spaces of irreducible symplectic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 404-434
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation