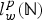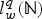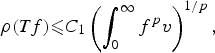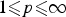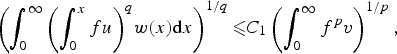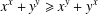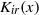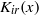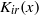Refine search
Actions for selected content:
7 results
106.29 An improvement on the Garfunkel-Bankoff inequality
- Part of
-
- Journal:
- The Mathematical Gazette / Volume 106 / Issue 566 / July 2022
- Published online by Cambridge University Press:
- 22 June 2022, pp. 342-344
- Print publication:
- July 2022
-
- Article
- Export citation
FKN theorem for the multislice, with applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 18 October 2019, pp. 200-212
-
- Article
- Export citation
Higher Summability and Discrete Weighted Muckenhoupt and Gehring Type Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 11 March 2019, pp. 949-973
-
- Article
- Export citation
Weighted norm inequalities for positive operators restricted on the cone of λ-quasiconcave functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 17-39
- Print publication:
- February 2020
-
- Article
- Export citation
NEW ALGEBRAIC-TRIGONOMETRIC INEQUALITIES OF LAUB–ILANI TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 87-97
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Bounds and algorithms for the
 $K$ -Bessel function of imaginary order
$K$ -Bessel function of imaginary order
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 78-108
-
- Article
-
- You have access
- Export citation
Some completely monotonic functions involving the gamma and polygamma functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-88
- Print publication:
- February 2006
-
- Article
-
- You have access
- Export citation