Many Banach algebras A have the property that, although there are discontinuous homomorphisms from A into other Banach algebras, every homomorphism from A into another Banach algebra is automatically continuous on a dense subspace—preferably, a subalgebra—of A. Examples of such algebras are C*-algebras and the group algebras L1(G), where G is a locally compact, abelian group. In this paper, we prove analogous results for 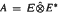 , where E is a Banach space, and
, where E is a Banach space, and 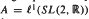 . An important rôle is played by the second Hochschild cohomology group of
. An important rôle is played by the second Hochschild cohomology group of 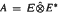 and
and 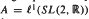 , respectively, with coefficients in the one-dimensional annihilator module. It vanishes in the first case and has linear dimension one in the second one.
, respectively, with coefficients in the one-dimensional annihilator module. It vanishes in the first case and has linear dimension one in the second one.
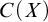 $C(X)$ WITH
$C(X)$ WITH 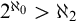 $2^{\aleph _0}>\aleph _2$
$2^{\aleph _0}>\aleph _2$
 $^{\ast }$-ALGEBRAS
$^{\ast }$-ALGEBRAS