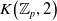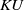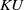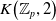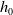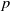Refine search
Actions for selected content:
3 results
The connective
 $K$-theory of the Eilenberg–MacLane space
$K$-theory of the Eilenberg–MacLane space 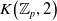 $K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
$K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 188-220
- Print publication:
- January 2024
-
- Article
- Export citation
MORAVA K-THEORY AND FILTRATIONS BY POWERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1-77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE GROMOV-LAWSON-ROSENBERG CONJECTURE FOR THE SEMI-DIHEDRAL GROUP OF ORDER 16
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 365-386
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation