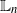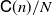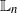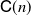Refine search
Actions for selected content:
5 results
Stopping problems with an unknown state
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 09 August 2023, pp. 515-528
- Print publication:
- June 2024
-
- Article
- Export citation
Log-normalization constant estimation using the ensemble Kalman–Bucy filter with application to high-dimensional models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. 1139-1163
- Print publication:
- December 2022
-
- Article
- Export citation
Computational Inference Beyond Kingman's Coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 519-537
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
A uniformly convergent adaptive particle filter
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1053-1068
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Distribution-free confidence intervals for measurement of effective bandwidth
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 224-235
- Print publication:
- March 2000
-
- Article
- Export citation