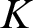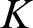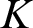In 2001, the algebraico-tree-theoretic simplicity hierarchical structure of J. H. Conway’s ordered field ${\mathbf {No}}$ of surreal numbers was brought to the fore by the first author and employed to provide necessary and sufficient conditions for an ordered field (ordered $K$-vector space) to be isomorphic to an initial subfield ($K$-subspace) of ${\mathbf {No}}$, i.e. a subfield ($K$-subspace) of ${\mathbf {No}}$ that is an initial subtree of ${\mathbf {No}}$. In this sequel, analogous results are established for ordered exponential fields, making use of a slight generalization of Schmeling’s conception of a transseries field. It is further shown that a wide range of ordered exponential fields are isomorphic to initial exponential subfields of 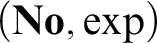$({\mathbf {No}}, \exp )$. These include all models of 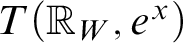$T({\mathbb R}_W, e^x)$, where 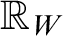${\mathbb R}_W$ is the reals expanded by a convergent Weierstrass system W. Of these, those we call trigonometric-exponential fields are given particular attention. It is shown that the exponential functions on the initial trigonometric-exponential subfields of ${\mathbf {No}}$, which includes ${\mathbf {No}}$ itself, extend to canonical exponential functions on their surcomplex counterparts. The image of the canonical map of the ordered exponential field 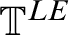${\mathbb T}^{LE}$ of logarithmic-exponential transseries into ${\mathbf {No}}$ is shown to be initial, as are the ordered exponential fields 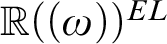${\mathbb R}((\omega ))^{EL}$ and 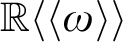${\mathbb R}\langle \langle \omega \rangle \rangle $.

Let T be a complete o-minimal extension of the theory of real closed fields. We characterize the convex hulls of elementary substructures of models of T and show that the residue field of such a convex hull has a natural expansion to a model of T. We give a quantifier elimination relative to T for the theory of pairs (ℛ, V) where ℛ ⊨ T and V ≠ ℛ is the convex hull of an elementary substructure of ℛ. We deduce that the theory of such pairs is complete and weakly o-minimal. We also give a quantifier elimination relative to T for the theory of pairs with ℛ a model of T and a proper elementary substructure that is Dedekind complete in ℛ. We deduce that the theory of such “tame” pairs is complete.

The results obtained extend Madden’s result for Dedekind domains to more general types of 1-dimensional Noetherian rings. In particular, these results apply to piecewise polynomial functions t:C → R where R is a real closed field and C ⊆ Rn is a closed 1-dimensional semi-algebraic set, and also to the associated “relative” case where t, C are defined over some subfield K ⊆ R.