We prove a general principle satisfied by weakly precompact sets of Lipschitz-free spaces. By this principle, certain infinite dimensional phenomena in Lipschitz-free spaces over general metric spaces may be reduced to the same phenomena in free spaces over their compact subsets. As easy consequences we derive several new and some known results. The main new results are: $\mathcal {F}(X)$ is weakly sequentially complete for every superreflexive Banach space $X$, and $\mathcal {F}(M)$ has the Schur property and the approximation property for every scattered complete metric space $M$.

We investigate the isomorphic structure of the Cesàro spaces and their duals, the Tandori spaces. The main result states that the Cesàro function space $\text{Ces}_{\infty }$ and its sequence counterpart $\text{ces}_{\infty }$ are isomorphic. This is rather surprising since $\text{Ces}_{\infty }$ (like Talagrand’s example) has no natural lattice predual. We prove that $\text{ces}_{\infty }$ is not isomorphic to $\ell _{\infty }$ nor is $\text{Ces}_{\infty }$ isomorphic to the Tandori space $\widetilde{L_{1}}$ with the norm $\Vert f\Vert _{\widetilde{L_{1}}}=\Vert \widetilde{f}\Vert _{L_{1}}$, where $\widetilde{f}(t):=\text{ess}\,\sup _{s\geqslant t}|f(s)|$. Our investigation also involves an examination of the Schur and Dunford–Pettis properties of Cesàro and Tandori spaces. In particular, using results of Bourgain we show that a wide class of Cesàro–Marcinkiewicz and Cesàro–Lorentz spaces have the latter property.

J. Elton used an application of Ramsey theory to show that if 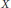$X$ is an infinite dimensional Banach space, then 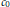${{c}_{0}}$ embeds in 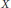$X$ , 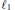${{\ell }_{1}}$ embeds in 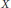$X$ , or there is a subspace of 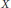$X$ that fails to have the Dunford–Pettis property. Bessaga and Pelczynski showed that if 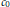${{c}_{0}}$ embeds in 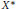${{X}^{*}}$ , then 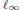${{\ell }_{\infty }}$ embeds in 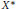${{X}^{*}}.$ Emmanuele and John showed that if 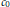${{c}_{0}}$ embeds in 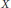$K\left( X,\,Y \right)$ , then 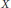$K\left( X,\,Y \right)$ is not complemented in 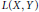$L\left( X,\,Y \right)$ . Classical results from Schauder basis theory are used in a study of Dunford–Pettis sets and strong Dunford–Pettis sets to extend each of the preceding theorems. The space 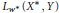${{L}_{{{w}^{*}}}}\left( {{X}^{*}},\,Y \right)$ of 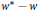${{w}^{*}}\,-\,w$ continuous operators is also studied.