Refine search
Actions for selected content:
20 results
First-passage times of two-dimensional Brownian motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1045-1060
- Print publication:
- December 2016
-
- Article
- Export citation
On ageing properties of first-passage times of increasing Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 241-259
- Print publication:
- March 2002
-
- Article
- Export citation
Ageing first-passage times of Markov processes: a matrix approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-13
- Print publication:
- March 1997
-
- Article
- Export citation
An operational calculus for probability distributions via Laplace transforms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 75-113
- Print publication:
- March 1996
-
- Article
- Export citation
A logarithmic reduction algorithm for quasi-birth-death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 650-674
- Print publication:
- September 1993
-
- Article
- Export citation
New better than used in expectation processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 116-128
- Print publication:
- March 1992
-
- Article
- Export citation
Applications of generalized inverses to Markov chains
-
- Journal:
- Advances in Applied Probability / Volume 23 / Issue 2 / June 1991
- Published online by Cambridge University Press:
- 01 July 2016, pp. 293-302
- Print publication:
- June 1991
-
- Article
- Export citation
A jump-driven Markovian electric load model
-
- Journal:
- Advances in Applied Probability / Volume 22 / Issue 3 / September 1990
- Published online by Cambridge University Press:
- 01 July 2016, pp. 564-586
- Print publication:
- September 1990
-
- Article
- Export citation
Cumulative shock models
-
- Journal:
- Advances in Applied Probability / Volume 22 / Issue 2 / June 1990
- Published online by Cambridge University Press:
- 01 July 2016, pp. 504-507
- Print publication:
- June 1990
-
- Article
-
- You have access
- Export citation
NBUE and NWUE properties of increasing Markov processes
-
- Journal:
- Journal of Applied Probability / Volume 26 / Issue 4 / December 1989
- Published online by Cambridge University Press:
- 14 July 2016, pp. 827-834
- Print publication:
- December 1989
-
- Article
- Export citation
On reinforcement-depletion compartmental urn models
-
- Journal:
- Journal of Applied Probability / Volume 26 / Issue 3 / September 1989
- Published online by Cambridge University Press:
- 14 July 2016, pp. 477-489
- Print publication:
- September 1989
-
- Article
- Export citation
Second-order approximations for certain stopped sums in extended renewal theory
-
- Journal:
- Advances in Applied Probability / Volume 20 / Issue 2 / June 1988
- Published online by Cambridge University Press:
- 01 July 2016, pp. 391-410
- Print publication:
- June 1988
-
- Article
- Export citation
Transient behavior of the M/M/1 queue via Laplace transforms
-
- Journal:
- Advances in Applied Probability / Volume 20 / Issue 1 / March 1988
- Published online by Cambridge University Press:
- 01 July 2016, pp. 145-178
- Print publication:
- March 1988
-
- Article
- Export citation
Transient behavior of regulated Brownian motion, I: Starting at the origin
-
- Journal:
- Advances in Applied Probability / Volume 19 / Issue 3 / September 1987
- Published online by Cambridge University Press:
- 01 July 2016, pp. 560-598
- Print publication:
- September 1987
-
- Article
- Export citation
A class of correlated cumulative shock models
-
- Journal:
- Advances in Applied Probability / Volume 17 / Issue 2 / June 1985
- Published online by Cambridge University Press:
- 01 July 2016, pp. 347-366
- Print publication:
- June 1985
-
- Article
- Export citation
Finite birth-and-death models in randomly changing environments
-
- Journal:
- Advances in Applied Probability / Volume 16 / Issue 4 / December 1984
- Published online by Cambridge University Press:
- 01 July 2016, pp. 715-731
- Print publication:
- December 1984
-
- Article
- Export citation
On conditional passage time structure of birth-death processes
-
- Journal:
- Journal of Applied Probability / Volume 21 / Issue 1 / March 1984
- Published online by Cambridge University Press:
- 14 July 2016, pp. 10-21
- Print publication:
- March 1984
-
- Article
- Export citation
The stochastic geyser problem for first-passage times
-
- Journal:
- Journal of Applied Probability / Volume 18 / Issue 1 / March 1981
- Published online by Cambridge University Press:
- 14 July 2016, pp. 91-103
- Print publication:
- March 1981
-
- Article
- Export citation
The exact order of normal approximation in bivariate renewal theory
-
- Journal:
- Advances in Applied Probability / Volume 13 / Issue 1 / March 1981
- Published online by Cambridge University Press:
- 01 July 2016, pp. 113-128
- Print publication:
- March 1981
-
- Article
- Export citation
Some mean first-passage time approximations for the Ornstein-Uhlenbeck process
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 3 / September 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 600-604
- Print publication:
- September 1975
-
- Article
- Export citation
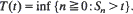
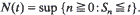
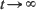 . All descriptions of the transient behavior are expressed in terms of basic building blocks such as the first-passage-time distributions. The analysis is facilitated by appropriate scaling of space and time so that regulated or reflected Brownian motion (RBM) appears as the special case in which the traffic intensity ρ equals the critical value 1. An operational calculus is developed for obtaining
. All descriptions of the transient behavior are expressed in terms of basic building blocks such as the first-passage-time distributions. The analysis is facilitated by appropriate scaling of space and time so that regulated or reflected Brownian motion (RBM) appears as the special case in which the traffic intensity ρ equals the critical value 1. An operational calculus is developed for obtaining 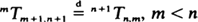 , for
, for 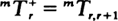 is considerably different from that of the ordinary first-passage time
is considerably different from that of the ordinary first-passage time 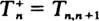 where, under certain conditions, exponentiality sets in as
where, under certain conditions, exponentiality sets in as 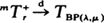 as
as 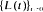 of first-passage times. More precisely, it is shown that a single realization of the sequence
of first-passage times. More precisely, it is shown that a single realization of the sequence 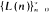 determines the distribution function (d.f.) of the
determines the distribution function (d.f.) of the 