Refine search
Actions for selected content:
6 results
Ladder epochs and ladder chain of a Markov random walk with discrete driving chain
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 31-46
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Quasistochastic matrices and Markov renewal theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 359-376
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A Self-Normalized Central Limit Theorem for Markov Random Walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 452-478
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Asymptotic expansions in multidimensional Markov renewal theory and first passage times for Markov random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 652-673
- Print publication:
- September 2001
-
- Article
- Export citation
Wald's equations, first passage times and moments of ladder variables in Markov random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 566-580
- Print publication:
- September 1998
-
- Article
- Export citation
Corrected Diffusion Approximations for Ruin Probabilities in a Markov Random Walk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 695-712
- Print publication:
- September 1997
-
- Article
- Export citation
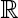 , and is adjoined to the chain such that {
, and is adjoined to the chain such that {