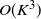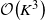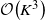Refine search
Actions for selected content:
7 results
Strategies in the multi-armed bandit
-
- Journal:
- Experimental Economics ,
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Crowdsourced Adaptive Surveys
-
- Journal:
- Political Analysis / Volume 33 / Issue 4 / October 2025
- Published online by Cambridge University Press:
- 12 February 2025, pp. 284-297
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conditions for indexability of restless bandits and an
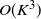 $O(K^3)$ algorithm to compute whittle index – CORRIGENDUM
$O(K^3)$ algorithm to compute whittle index – CORRIGENDUM
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 1473-1474
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
Conditions for indexability of restless bandits and an
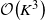 $\mathcal{O}\!\left(K^3\right)$ algorithm to compute Whittle index
$\mathcal{O}\!\left(K^3\right)$ algorithm to compute Whittle index
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1164-1192
- Print publication:
- December 2022
-
- Article
- Export citation
Optimal stochastic scheduling of forest networks with switching penalties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 474-497
- Print publication:
- June 1994
-
- Article
- Export citation
Optimality of index policies for stochastic scheduling with switching penalties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 957-966
- Print publication:
- December 1992
-
- Article
- Export citation
Restless bandits: activity allocation in a changing world
-
- Journal:
- Journal of Applied Probability / Volume 25 / Issue A / 1988
- Published online by Cambridge University Press:
- 14 July 2016, pp. 287-298
- Print publication:
- 1988
-
- Article
- Export citation