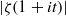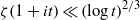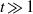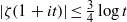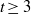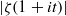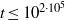Refine search
Actions for selected content:
10 results
On the Hilbert space derived from the Weil distribution
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential sums over Möbius convolutions with applications to partitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-36
-
- Article
- Export citation
BOUNDING ZETA ON THE 1-LINE UNDER THE PARTIAL RIEMANN HYPOTHESIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 10 January 2024, pp. 244-251
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NEW EFFECTIVE RESULTS IN THE THEORY OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 403-406
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
A HARMONIC SUM OVER NONTRIVIAL ZEROS OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 20 November 2020, pp. 59-65
- Print publication:
- August 2021
-
- Article
- Export citation
Approximating the Riemann Zeta-function by Polynomials with Restricted Zeros
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 475-478
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
A NEW UPPER BOUND FOR
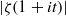 $\vert \zeta (1+ it)\vert $
$\vert \zeta (1+ it)\vert $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 259-264
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ON A CERTAIN CONVOLUTION OF POLYLOGARITHMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 461-472
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
EVALUATION OF CERTAIN CLASSES OF EISENSTEIN-TYPE SERIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 239-247
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
ON THE PAIR CORRELATION OF ZEROS OF THE RIEMANN ZETA-FUNCTION
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 80 / Issue 1 / January 2000
- Published online by Cambridge University Press:
- 01 January 2000, pp. 31-49
- Print publication:
- January 2000
-
- Article
- Export citation