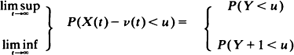Refine search
Actions for selected content:
7 results
Log-concavity and log-convexity of moments of averages of i.i.d. random variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 271-278
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On domains of partial attraction
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 328-331
-
- Article
-
- You have access
- Export citation
Toward the best constant factorfor the Rademacher-Gaussian tail comparison
-
- Journal:
- ESAIM: Probability and Statistics / Volume 11 / June 2007
- Published online by Cambridge University Press:
- 17 August 2007, pp. 412-426
- Print publication:
- June 2007
-
- Article
- Export citation
On population-size-dependent branching processes
-
- Journal:
- Advances in Applied Probability / Volume 16 / Issue 1 / March 1984
- Published online by Cambridge University Press:
- 01 July 2016, pp. 30-55
- Print publication:
- March 1984
-
- Article
- Export citation
Another look at the finite mean supercritical Bienaymé–Galton–Watson process
-
- Journal:
- Journal of Applied Probability / Volume 19 / Issue A / 1982
- Published online by Cambridge University Press:
- 14 July 2016, pp. 307-312
- Print publication:
- 1982
-
- Article
- Export citation
A non-Markovian birth process with logarithmic growth
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 4 / December 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 673-683
- Print publication:
- December 1975
-
- Article
- Export citation
A supplement to the strong law of large numbers
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 1 / March 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 173-175
- Print publication:
- March 1975
-
- Article
- Export citation
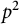
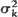 of offspring distribution stabilize as the population size
of offspring distribution stabilize as the population size 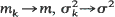 The process exhibits different asymptotic behaviour according to m < l,
The process exhibits different asymptotic behaviour according to m < l, 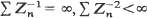 a.s. both on a set of non-extinction and there are no constants
a.s. both on a set of non-extinction and there are no constants 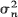 do not grow to ∞ faster than
do not grow to ∞ faster than 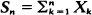 of independent random variables converges in distribution when suitably normalised, so long as the
of independent random variables converges in distribution when suitably normalised, so long as the