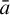Refine search
Actions for selected content:
3 results
QUASI-INVARIANT MEASURES CONCENTRATING ON COUNTABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the algebraicity about the Hodge numbers of the Hilbert schemes of algebraic surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 392-403
-
- Article
- Export citation
!ALGEBRAICITY AND TRANSCENDENCY OF BASIC SPECIAL VALUES OF SHINTANI’S DOUBLE SINE FUNCTIONS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 30 May 2006, pp. 361-366
-
- Article
-
- You have access
- Export citation