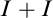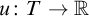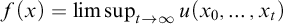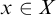Refine search
Actions for selected content:
5 results
1 - Preliminaries
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 24-33
-
- Chapter
- Export citation
A ONE-PAGE PROOF OF A THEOREM OF BELEZNAY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 18 March 2025, pp. 536-537
- Print publication:
- December 2024
-
- Article
- Export citation
GAMES CHARACTERIZING LIMSUP FUNCTIONS AND BAIRE CLASS 1 FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1459-1473
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - Measurable and Non-Measurable Sets
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 138-163
-
- Chapter
- Export citation
DELAYS, RECURRENCE AND ORDINALS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 82 / Issue 2 / March 2001
- Published online by Cambridge University Press:
- 05 March 2001, pp. 257-298
- Print publication:
- March 2001
-
- Article
- Export citation