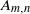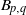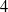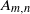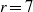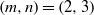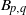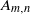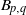Refine search
Actions for selected content:
1 results
LENS SPACE SURGERIES ALONG CERTAIN 2-COMPONENT LINKS RELATED WITH PARK’S RATIONAL BLOW DOWN, AND REIDEMEISTER-TURAEV TORSION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 78-126
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
-
We study lens space surgeries along two different families of 2-component links, denoted by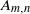
${A}_{m, n} $ and 
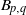${B}_{p, q} $, related with the rational homology 
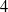$4$-ball used in J. Park’s (generalized) rational blow down. We determine which coefficient 
$r$ of the knotted component of the link yields a lens space by Dehn surgery. The link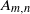 
${A}_{m, n} $ yields a lens space only by the known surgery with 
$r= mn$ and unexpectedly with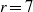 
$r= 7$ for 
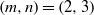$(m, n)= (2, 3)$. On the other hand, 
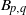${B}_{p, q} $ yields a lens space by infinitely many 
$r$. Our main tool for the proof are the Reidemeister-Turaev torsions, that is, Reidemeister torsions with combinatorial Euler structures. Our results can be extended to the links whose Alexander polynomials are same as those of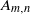 
${A}_{m, n} $ and 
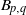${B}_{p, q} $.
