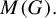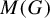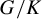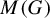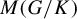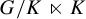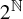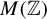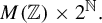Refine search
Actions for selected content:
5 results
EXPERIMENTAL STUDY ON THE CHARGE-EXCHANGE CROSS-SECTIONS OF LOW-ENERGY CARBON IONS IN HELIUM AT GXNU
-
- Journal:
- Radiocarbon / Volume 66 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 1417-1428
- Print publication:
- October 2024
-
- Article
- Export citation
5 - The Autocratic Legacy of Muslim Conquest
- from Part II - The Institutional Legacy of Muslim Conquest
-
- Book:
- Conquests and Rents
- Published online:
- 01 June 2023
- Print publication:
- 15 June 2023, pp 133-176
-
- Chapter
- Export citation
Universal minimal flows of extensions of and by compact groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 04 August 2022, pp. 2538-2548
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
12 - Scattering, the Scattering Matrix and Cross-Sections
- from Part III - Interactions
-
- Book:
- What Is a Quantum Field Theory?
- Published online:
- 22 February 2022
- Print publication:
- 17 March 2022, pp 322-350
-
- Chapter
- Export citation
Mechanisms of basin contraction and reactivation in the basement-involved Malargüe fold-and-thrust belt, Central Andes (34–36°S)
-
- Journal:
- Geological Magazine / Volume 153 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 28 July 2016, pp. 926-944
-
- Article
-
- You have access
- HTML
- Export citation