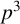Refine search
Actions for selected content:
3 results
WEIGHT CONJECTURES FOR FUSION SYSTEMS ON AN EXTRASPECIAL GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 02 February 2026, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In a previous paper, we stated and motivated counting conjectures for fusion systems that are purely local analogues of several local-to-global conjectures in the modular representation theory of finite groups. Here, we verify some of these conjectures for fusion systems on an extraspecial group of order
$p^3$, which contain among them the Ruiz–Viruel exotic fusion systems at the prime 
$7$. As a byproduct, we verify Robinson’s ordinary weight conjecture for principal p-blocks of almost simple groups G realizing such (nonconstrained) fusion systems.
Conditions for the supersolvability of
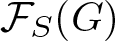$\mathcal{F}_{S}(G)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 23 January 2025, pp. 566-572
-
- Article
- Export citation
-
In this article,
$\mathcal{F}_{S}(G)$ denotes the fusion category of G on a Sylow p-subgroup S of G where p denotes a prime. A subgroup K of G has normal complement in G if there is a normal subgroup T of G satisfying that G = KT and 
$T \cap K = 1$. We investigate the supersolvability of 
$\mathcal{F}_{S}(G)$ under the assumption that some subgroups of S are normal in G or have normal complement in G.
Splitting fusion systems over 2-groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 263-301
-
- Article
-
- You have access
- Export citation
