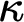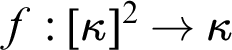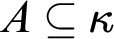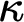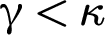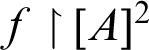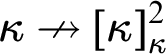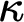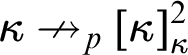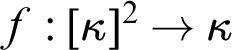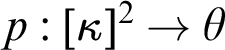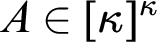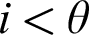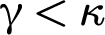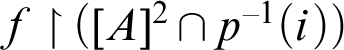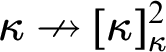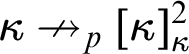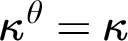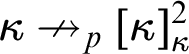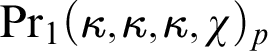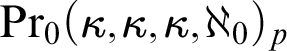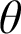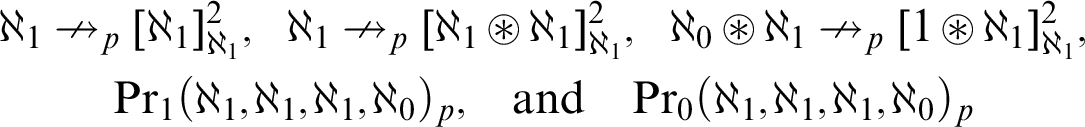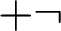A strong coloring on a cardinal 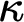 $\kappa $ is a function
$\kappa $ is a function 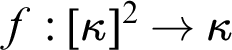 $f:[\kappa ]^2\to \kappa $ such that for every
$f:[\kappa ]^2\to \kappa $ such that for every 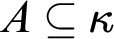 $A\subseteq \kappa $ of full size
$A\subseteq \kappa $ of full size 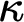 $\kappa $, every color
$\kappa $, every color 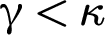 $\unicode{x3b3} <\kappa $ is attained by
$\unicode{x3b3} <\kappa $ is attained by 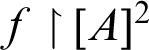 $f\restriction [A]^2$. The symbol
$f\restriction [A]^2$. The symbol 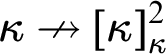 $$ \begin{align*} \kappa\nrightarrow[\kappa]^2_{\kappa} \end{align*} $$
$$ \begin{align*} \kappa\nrightarrow[\kappa]^2_{\kappa} \end{align*} $$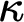 $\kappa $.
$\kappa $.
We introduce the symbol 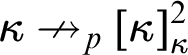 $$ \begin{align*} \kappa\nrightarrow_p[\kappa]^2_{\kappa} \end{align*} $$
$$ \begin{align*} \kappa\nrightarrow_p[\kappa]^2_{\kappa} \end{align*} $$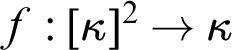 $f:[\kappa ]^2\to \kappa $ which is strong over a partition
$f:[\kappa ]^2\to \kappa $ which is strong over a partition 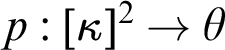 $p:[\kappa ]^2\to \theta $. A coloring f is strong over p if for every
$p:[\kappa ]^2\to \theta $. A coloring f is strong over p if for every 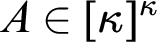 $A\in [\kappa ]^{\kappa }$ there is
$A\in [\kappa ]^{\kappa }$ there is 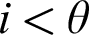 $i<\theta $ so that for every color
$i<\theta $ so that for every color 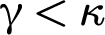 $\unicode{x3b3} <\kappa $ is attained by
$\unicode{x3b3} <\kappa $ is attained by 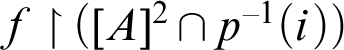 $f\restriction ([A]^2\cap p^{-1}(i))$.
$f\restriction ([A]^2\cap p^{-1}(i))$.
We prove that whenever 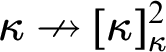 $\kappa \nrightarrow [\kappa ]^2_{\kappa }$ holds, also
$\kappa \nrightarrow [\kappa ]^2_{\kappa }$ holds, also 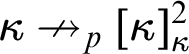 $\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$ holds for an arbitrary finite partition p. Similarly, arbitrary finite p-s can be added to stronger symbols which hold in any model of ZFC. If
$\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$ holds for an arbitrary finite partition p. Similarly, arbitrary finite p-s can be added to stronger symbols which hold in any model of ZFC. If 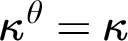 $\kappa ^{\theta }=\kappa $, then
$\kappa ^{\theta }=\kappa $, then 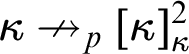 $\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$ and stronger symbols, like
$\kappa \nrightarrow _p[\kappa ]^2_{\kappa }$ and stronger symbols, like 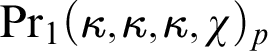 $\operatorname {Pr}_1(\kappa ,\kappa ,\kappa ,\chi )_p$ or
$\operatorname {Pr}_1(\kappa ,\kappa ,\kappa ,\chi )_p$ or 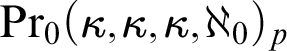 $\operatorname {Pr}_0(\kappa ,\kappa ,\kappa ,\aleph _0)_p$, also hold for an arbitrary partition p to
$\operatorname {Pr}_0(\kappa ,\kappa ,\kappa ,\aleph _0)_p$, also hold for an arbitrary partition p to 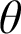 $\theta $ parts.
$\theta $ parts.
The symbols 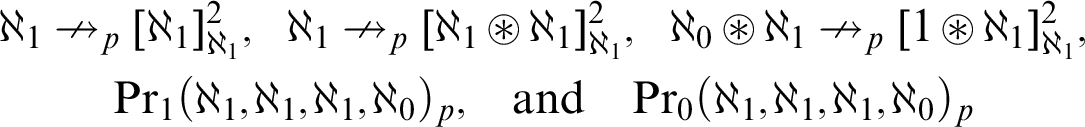 $$ \begin{gather*} \aleph_1\nrightarrow_p[\aleph_1]^2_{\aleph_1},\;\;\; \aleph_1\nrightarrow_p[\aleph_1\circledast \aleph_1]^2_{\aleph_1},\;\;\; \aleph_0\circledast\aleph_1\nrightarrow_p[1\circledast\aleph_1]^2_{\aleph_1}, \\ \operatorname{Pr}_1(\aleph_1,\aleph_1,\aleph_1,\aleph_0)_p,\;\;\;\text{ and } \;\;\; \operatorname{Pr}_0(\aleph_1,\aleph_1,\aleph_1,\aleph_0)_p \end{gather*} $$
$$ \begin{gather*} \aleph_1\nrightarrow_p[\aleph_1]^2_{\aleph_1},\;\;\; \aleph_1\nrightarrow_p[\aleph_1\circledast \aleph_1]^2_{\aleph_1},\;\;\; \aleph_0\circledast\aleph_1\nrightarrow_p[1\circledast\aleph_1]^2_{\aleph_1}, \\ \operatorname{Pr}_1(\aleph_1,\aleph_1,\aleph_1,\aleph_0)_p,\;\;\;\text{ and } \;\;\; \operatorname{Pr}_0(\aleph_1,\aleph_1,\aleph_1,\aleph_0)_p \end{gather*} $$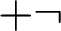 $+ \neg $CH.
$+ \neg $CH.