For a 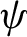$\psi $-mixing process 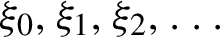$\xi _0,\xi _1,\xi _2,\ldots $ we consider the number 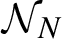${\mathcal N}_N$ of multiple returns 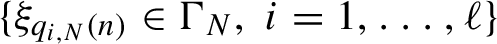$\{\xi _{q_{i,N}(n)}\in {\Gamma }_N,\, i=1,\ldots ,\ell \}$ to a set 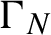${\Gamma }_N$ for n until either a fixed number N or until the moment 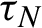$\tau _N$ when another multiple return 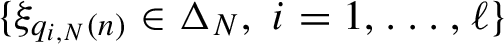$\{\xi _{q_{i,N}(n)}\in {\Delta }_N,\, i=1,\ldots ,\ell \}$, takes place for the first time where 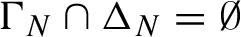${\Gamma }_N\cap {\Delta }_N=\emptyset $ and 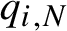$q_{i,N}$, 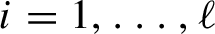$i=1,\ldots ,\ell $ are certain functions of n taking on non-negative integer values when n runs from 0 to N. The dependence of 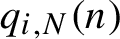$q_{i,N}(n)$ on both n and N is the main novelty of the paper. 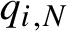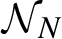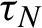Under some restrictions on the functions $q_{i,N}$ we obtain Poisson distributions limits of ${\mathcal N}_N$ when counting is until N as $N\to \infty $ and geometric distributions limits when counting is until $\tau _N$ as $N\to \infty $. We obtain also similar results in the dynamical systems setup considering a 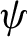$\psi $-mixing shift T on a sequence space ${\Omega }$ and studying the number of multiple returns 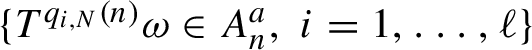$\{ T^{q_{i,N}(n)}{\omega }\in A^a_n,\, i=1,\ldots ,\ell \}$ until the first occurrence of another multiple return 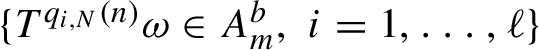$\{ T^{q_{i,N}(n)}{\omega }\in A^b_m,\, i=1,\ldots ,\ell \}$ where 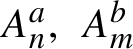$A^a_n,\, A_m^b$ are cylinder sets of length n and m constructed by sequences 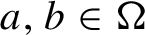$a,b\in {\Omega }$, respectively, and chosen so that their probabilities have the same order.