We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Soient K un corps discrètement valué et hensélien, 
${\mathcal {O}}$ son anneau d’entiers supposé excellent,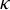 
$\kappa $ son corps résiduel supposé parfait et G un K-groupe quasi-réductif, c’est-à-dire lisse, affine, connexe et à radical unipotent déployé trivial. On construit l’immeuble de Bruhat-Tits 
${\mathcal {I}}(G, K)$ pour 
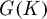$G(K)$ de façon canonique, améliorant les constructions moins canoniques de M. Solleveld sur les corps locaux, et l’on associe un 
${\mathcal {O}}$-modèle en groupes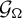 
${\mathcal {G}}_{\Omega }$ de G à chaque partie non vide et bornée 
$\Omega $ contenue dans un appartement de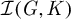 
${\mathcal {I}}(G,K)$. On montre que les groupes parahoriques 
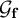${\mathcal {G}}_{\textbf {f}}$ attachés aux facettes peuvent être caractérisés en fonction de la géométrie de leurs grassmanniennes affines, ainsi que dans la thèse de T. Richarz. Ces résultats sont appliqués ailleurs à l’étude des grassmanniennes affines tordues entières.
