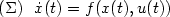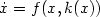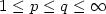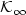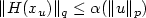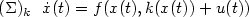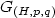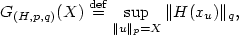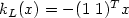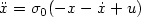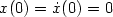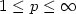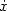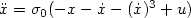This paper considers the guidance issue for attackers against aircraft with active defense in a two-on-two engagement, which includes an attacker, a protector, a defender and a target. A cooperative line-of-sight guidance scheme with prescribed performance and input saturation is proposed utilising the sliding mode control and line-of-sight guidance theories, which guarantees that the attacker is able to capture the target with the assistance of the protector remaining on the line-of-sight between the defender and the attacker in order to intercept the defender. A fixed-time prescribed performance function and first-order anti-saturation auxiliary variable are designed in the game guidance strategy to constrain the overshoot of the guidance variable and satisfy the requirement of an overload manoeuver. The proposed guidance strategy alleviates the influence of external disturbance by implementing a fixed-time observer and the chattering phenomenon caused by the sign function. Finally, nonlinear numerical simulations verify the cooperative guidance strategies.

In this paper, we propose a novel vision-based adaptive leakage-type (LT) sliding mode admittance control for actuator-constrained collaborative robots to realize the synchronous control of the precise path following and compliant interaction force. Firstly, we develop a vision-admittance-based model to couple the visual feedback and force sensing in the image feature space so that a reference image feature trajectory can be obtained concerning the contact force command and predefined trajectory. Secondly, considering the system uncertainty, external disturbance, and torque constraints of collaborative robots in reality, we propose an adaptive sliding mode controller in the image feature space to perform precise trajectory tracking. This controller employs a leakage-type (LT) adaptive control law to reduce the side effects of system uncertainties without knowing the upper bound of system uncertainties. Moreover, an auxiliary dynamic is considered in this controller to overcome the joint torque constraints. Finally, we prove the convergence of the tracking error with the Lyapunov stability analysis and operate various semi-physical simulations compared to the conventional adaptive sliding mode and parallel vision/force controller to demonstrate the efficacy of the proposed controller. The simulation results show that compared with the controller mentioned above, the path following accuracy and interaction force control precision of the proposed controller increased by 50% and achieved faster convergence.

A model-free adaptive robust control based on time delay estimation (TDE) is proposed for robot in the presence of disturbance and input saturation. TDE is utilized to estimate the complicated nonlinear terms of the robot including unknown dynamics and disturbance, and a TDE error observer is developed to estimate the inevitable TDE error. When the input torque of the robot exceeds the upper or lower limit of the input saturation, an auxiliary system and a saturation deviation boundary adaptive law are employed to mitigate the negative impact of input saturation on the position tracking. Finally, the robust control law is obtained by backstepping. The stability of the closed-loop system is proved by Lyapunov functions, and the validity of the proposed method is demonstrated by comparative simulations and experiments. Compared with the model-based controllers and other model-free controllers, the proposed method does not necessitate the accurate dynamic model of the complicated system and with lower computation. Moreover, it can guarantee the desired position tracking performance of the robot even subject to disturbance and input saturation simultaneously.

This paper explores finite-time formation control of multi-agent systems (MASs) with high-order nonaffine nonlinear dynamics and saturated input. Based on active disturbance rejection control theory, extended state observer is employed to identify unknown nonaffine nonlinear functions in MASs. The proposed control law consisting of backstepping control, tracking differentiator, and finite-time performance function is adopted for MASs to achieve the desired formation while reaching performance requirements. An auxiliary dynamic compensator is introduced to correct the control deviation caused by input saturation. Lyapunov stability theory is utilized to analyze the stability of the closed-loop system, which guarantees that the formation tracking error can asymptotically converge to an arbitrarily small neighborhood around zero in finite time. Finally, the simulation results show that compared to the adaptive, cooperative learning, and virtual structure methods, the proposed control algorithm has stronger tracking ability and faster setting time (1.8 s) under the influence of nonaffine nonlinear uncertainties. The integral square error for the formation control strategy in this paper is 0.16, which is much smaller than the abovementioned methods and is therefore provided to manifest the validity and feasibility of the proposed control strategy.

Saturation nonlinearities, among the known challenges in control engineering, are ubiquitous in robotic systems and can lead to stability and performance degradation. In this paper, an adaptive dynamic surface impedance (ADSI) control approach is developed for an n-link robotic manipulator by employing self-recurrent wavelet neural networks (SRWNNs) in order to overcome the saturation effect. The proposed control approach is inspired by the theory of dynamic surface control (DSC) and SRWNNs. As a novel application of the dynamic surface method to obtain a simple structure, the target impedance is formulated in the state–space, and effective dynamic surfaces are defined to track the desired impedance behavior. In fact, DSC is used to force the robot manipulator to track the desired impedance, while the robot interacts with an environment. In addition, SRWNNs are applied to approximate the parametric uncertainties and external disturbances in the robot dynamical model. Self-feedback neurons are embedded as memory units in SRWNNs to model the sudden dynamic jumps of the environment. Using Lyapunov's method, an ADSI controller is designed, and adaptation laws are induced to guarantee the stability of the closed-loop system. Finally, simulations are conducted to verify the proper performance of the proposed approach for removing the saturation effect and tracking the target impedance. It is worth noting that the simulation results indicate the robustness of the controller against uncertainties and external disturbances.

Since a slave manipulator with a high reduction ratio joint generally has slow dynamics in comparison with a master manipulator in telemanipulation systems, its control input is likely to be saturated resulting in poor position tracking performance and deteriorated stability. This paper proposes a force reflecting control scheme for telemanipulators with a high reduction ratio joint, which can effectively compensate the control input saturation caused by the high ratio gear reducer at its joint. The proposed scheme is also shown to guarantee the stability and provides an excellent position tracking performance regardless of the saturation.

We consider a finite-dimensional control system $(\Sigma)\ \ \dotx(t)=f(x(t),u(t))$ 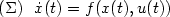, such that there exists a feedback stabilizer kthat renders $\dot x=f(x,k(x))$ 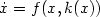globally asymptoticallystable. Moreover,for (H,p,q) with H an output map and $1\leqp\leq q\leq \infty$ 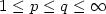, we assume that there exists a ${\cal {K}}_{\infty}$ 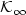-functionα such that $\|H(x_u)\|_q\leq \alpha(\|u\|_p)$ 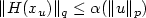, where x u is themaximal solution of $(\Sigma)_k \ \ \dot x(t)=f(x(t),k(x(t))+u(t))$ 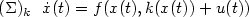,corresponding to u and to the initial condition x(0)=0. Then, thegain function $G_{(H,p,q)}$ 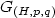of (H,p,q) given by 14.5cm $$G_{(H,p,q)}(X)\stackrel{\rm def}{=}\sup_{\|u\|_p=X}\|H(x_u)\|_q,$$ 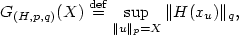is well-defined. We call profile of k for (H,p,q) any ${\cal {K}}_{\infty}$ 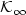-function which is of the same order of magnitude as $G_{(H,p,q)}$ 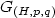. For the double integrator subject to input saturation and stabilized by $k_L(x)=-(1\1)^Tx$ 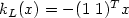, we determine the profiles corresponding to the mainoutput maps. In particular, if $\sigma_0$ 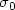is used to denote the standardsaturation function, we show that the L 2-gain from the output of the saturation nonlinearity to u of the system $\ddot x=\sigma_0(-x-\dot x+u)$ 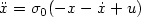with $x(0)= \dot x(0)=0$ 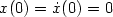, is finite. We also provide a class of feedback stabilizers k F that have a linear profile for (x,p,p), $1\leq p\leq \infty$ 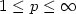. For instance,we show that the L 2-gains from x and $\dot x$ 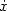to u of the system $\ddot x=\sigma_0(-x-\dot x-(\dot x)^3+u)$ 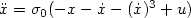with $x(0)= \dot x(0)=0$ 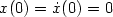, are finite.