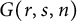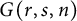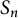Refine search
Actions for selected content:
1 results
Polynomiality of factorizations in reflection groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 245-266
- Print publication:
- February 2023
-
- Article
- Export citation