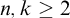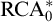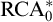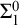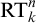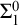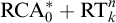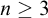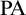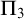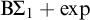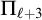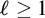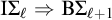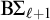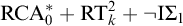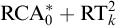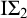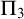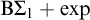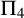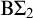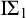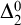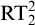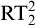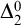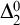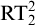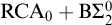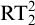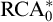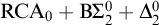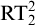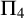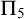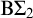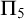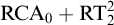We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the first-order consequences of Ramsey’s Theorem for k-colourings of n-tuples, for fixed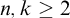 
$n, k \ge 2$, over the relatively weak second-order arithmetic theory 
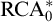$\mathrm {RCA}^*_0$. Using the Chong–Mourad coding lemma, we show that in a model of 
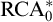$\mathrm {RCA}^*_0$ that does not satisfy 
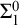$\Sigma ^0_1$ induction, 
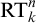$\mathrm {RT}^n_k$ is equivalent to its relativization to any proper 
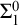$\Sigma ^0_1$-definable cut, so its truth value remains unchanged in all extensions of the model with the same first-order universe.
We give a complete axiomatization of the first-order consequences of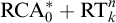 
$\mathrm {RCA}^*_0 + \mathrm {RT}^n_k$ for 
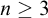$n \ge 3$. We show that they form a non-finitely axiomatizable subtheory of 
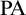$\mathrm {PA}$ whose 
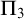$\Pi _3$ fragment coincides with 
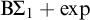$\mathrm {B} \Sigma _1 + \exp $ and whose 
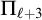$\Pi _{\ell +3}$ fragment for 
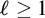$\ell \ge 1$ lies between 
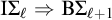$\mathrm {I} \Sigma _\ell \Rightarrow \mathrm {B} \Sigma _{\ell +1}$ and 
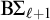$\mathrm {B} \Sigma _{\ell +1}$. We also give a complete axiomatization of the first-order consequences of 
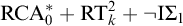$\mathrm {RCA}^*_0 + \mathrm {RT}^2_k + \neg \mathrm {I} \Sigma _1$. In general, we show that the first-order consequences of 
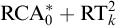$\mathrm {RCA}^*_0 + \mathrm {RT}^2_k$ form a subtheory of 
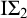$\mathrm {I} \Sigma _2$ whose 
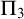$\Pi _3$ fragment coincides with 
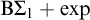$\mathrm {B} \Sigma _1 + \exp $ and whose 
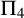$\Pi _4$ fragment is strictly weaker than 
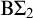$\mathrm {B} \Sigma _2$ but not contained in 
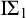$\mathrm {I} \Sigma _1$.
Additionally, we consider a principle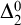 
$\Delta ^0_2$-
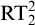$\mathrm {RT}^2_2$ which is defined like 
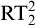$\mathrm {RT}^2_2$ but with both the 
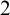$2$-colourings and the solutions allowed to be 
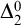$\Delta ^0_2$-sets rather than just sets. We show that the behaviour of 
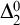$\Delta ^0_2$-
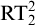$\mathrm {RT}^2_2$ over 
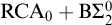$\mathrm {RCA}_0 + \mathrm {B}\Sigma ^0_2$ is in many ways analogous to that of 
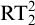$\mathrm {RT}^2_2$ over 
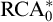$\mathrm {RCA}^*_0$, and that 
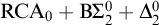$\mathrm {RCA}_0 + \mathrm {B} \Sigma ^0_2 + \Delta ^0_2$-
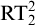$\mathrm {RT}^2_2$ is 
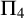$\Pi _4$- but not 
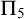$\Pi _5$-conservative over 
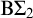$\mathrm {B} \Sigma _2$. However, the statement we use to witness failure of 
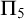$\Pi _5$-conservativity is not provable in 
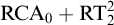$\mathrm {RCA}_0 +\mathrm {RT}^2_2$.
