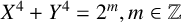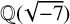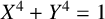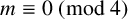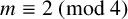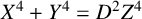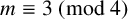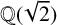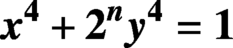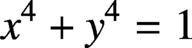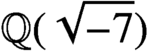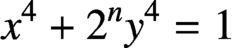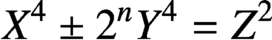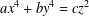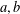In this paper, we generalise to the family of Fermat quartics 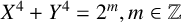 $X^4 + Y^4 = 2^m, m \in \mathbb {Z}$, a result of Aigner [‘Über die Möglichkeit von
$X^4 + Y^4 = 2^m, m \in \mathbb {Z}$, a result of Aigner [‘Über die Möglichkeit von  $x^4 + y^4 = z^4$ in quadratischen Körpern’, Jahresber. Deutsch. Math.-Ver. 43 (1934), 226–228], which proves that there is only one quadratic field, namely
$x^4 + y^4 = z^4$ in quadratischen Körpern’, Jahresber. Deutsch. Math.-Ver. 43 (1934), 226–228], which proves that there is only one quadratic field, namely 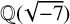 $\mathbb {Q}(\sqrt {-7})$, that contains solutions to the Fermat quartic
$\mathbb {Q}(\sqrt {-7})$, that contains solutions to the Fermat quartic 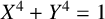 $X^4 + Y^4 = 1$. The
$X^4 + Y^4 = 1$. The 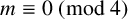 $m \equiv 0 \pmod 4$ case is due to Aigner. The
$m \equiv 0 \pmod 4$ case is due to Aigner. The 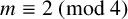 $m \equiv 2 \pmod 4$ case follows from a result of Emory [‘The Diophantine equation
$m \equiv 2 \pmod 4$ case follows from a result of Emory [‘The Diophantine equation 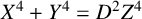 $X^4 + Y^4 = D^2Z^4$ in quadratic fields’, Integers 12 (2012), Article no. A65, 8 pages]. This paper focuses on the two cases
$X^4 + Y^4 = D^2Z^4$ in quadratic fields’, Integers 12 (2012), Article no. A65, 8 pages]. This paper focuses on the two cases  $m \equiv 1, 3 \pmod 4$, classifying for
$m \equiv 1, 3 \pmod 4$, classifying for  $m \equiv 1 \pmod 4$ the infinitely many quadratic number fields that contain solutions, and proving for
$m \equiv 1 \pmod 4$ the infinitely many quadratic number fields that contain solutions, and proving for 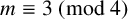 $m \equiv 3 \pmod 4$ that
$m \equiv 3 \pmod 4$ that 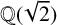 $\mathbb {Q}(\sqrt {2})$ and
$\mathbb {Q}(\sqrt {2})$ and  $\mathbb {Q}(\sqrt {-2})$ are the only quadratic number fields that contain solutions.
$\mathbb {Q}(\sqrt {-2})$ are the only quadratic number fields that contain solutions.
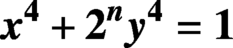 $\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
$\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS