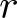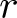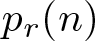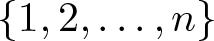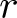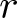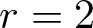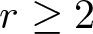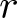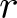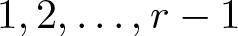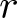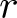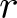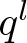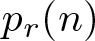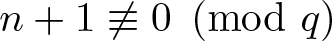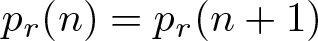Refine search
Actions for selected content:
1 results
Enriched cycle structures and roots of permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 January 2026, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
-
This paper is concerned with a duality between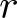
$r$-regular permutations and 
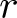$r$-cycle permutations, and a monotone property due to Bóna-McLennan-White on the probability 
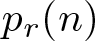$p_r(n)$ for a random permutation of 
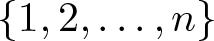$\{1,2,\ldots, n\}$ to have an 
$r$th root, where 
$r$ is a prime. For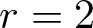 
$r=2$, the duality relates permutations with odd cycles to permutations with even cycles. For the general case where 
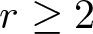$r\geq 2$, we define an 
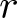$r$-enriched permutation as a permutation with 
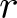$r$-singular cycles coloured by one of the colours 
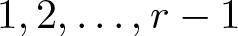$1, 2, \ldots, r-1 $. In this setup, we discover a bijection between 
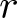$r$-regular permutations and enriched 
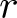$r$-cycle permutations, which in turn yields a stronger version of an inequality of Bóna-McLennan-White. This leads to a fully combinatorial understanding of the monotone property, thereby answering their question. When 
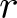$r$ is a prime power 
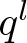$q^l$, we further show that 
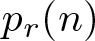$p_r(n)$ is monotone. In the case that 
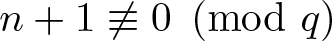$n+1 \not\equiv 0 \pmod q$, the equality 
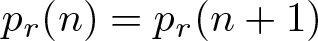$p_r(n)=p_r(n+1)$ has been established by Chernoff.
