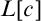Refine search
Actions for selected content:
5 results
APPROACHING A BRISTOL MODEL
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE ORDERING PRINCIPLE AND DEPENDENT CHOICE
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UPWARDS HOMOGENEITY IN ITERATED SYMMETRIC EXTENSIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 09 October 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REALIZING REALIZABILITY RESULTS WITH CLASSICAL CONSTRUCTIONS
-
- Journal:
- Bulletin of Symbolic Logic / Volume 25 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 19 December 2019, pp. 429-445
- Print publication:
- December 2019
-
- Article
- Export citation
ITERATING SYMMETRIC EXTENSIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 14 March 2019, pp. 123-159
- Print publication:
- March 2019
-
- Article
- Export citation